Реферат: Термодинамика растворов неметаллов в металлических расплавах

Реферат: Термодинамика растворов неметаллов в металлических расплавах

На правах рукописи

КРАСИН Валерий Павлович

ТЕРМОДИНАМИКА РАСТВОРОВ НЕМЕТАЛЛОВ

В МЕТАЛЛИЧЕСКИХ РАСПЛАВАХ И ЕЕ ПРИМЕНЕНИЕ

К ПРОЦЕССАМ НА ГРАНИЦЕ РАЗДЕЛА ТВЕРДЫЙ МЕТАЛЛ – МНОГОКОМПОНЕНТНЫЙ РАСПЛАВ

01.04.07 – «Физика конденсированного состояния»

АВТОРЕФЕРАТ

диссертации  на соискание ученой степени

 доктора физико-математических наук

Автор

Москва 2004

Работа выполнена в Московском государственном индустриальном

Университетете

Защита состоится « 26 » мая 2004 г. в 15 час. 00 мин.

на заседании диссертационного совета Д 212.130.04  МИФИпо адресу: 115409, г. Москва, Каширское шоссе, д. 31

С диссертацией можно ознакомиться в библиотеке МИФИ.

Автореферат разослан  «    »                       2004 г.

Просим принять участие в работе диссертационного совета или прислать отзыв в одном экземпляре, заверенный печатью организации, по адресу МИФИ.

Ученый секретарь

диссертационного совета МИФИ,

д.ф.-м.н., профессор                                                        Е.М. Кудрявцев

Актуальность проблемы. Поиск новых путей повышения служебных характеристик современных материалов и эффективных методов управления процессами, в которых используются жидкие металлы, в значительной степени связан с изучением физико-химических свойств металлических расплавов.

Кроме металлургии среди областей техники, где используют (или предполагают использовать) жидкие металлы необходимо отметить ядерные реакторы на быстрых нейтронах, термоядерные реакторы синтеза (ТЯР), МГД – генераторы, технологии полупроводниковых материалов.

Решение таких научно-технических задач, как подбор конструкционных материалов для работы в контакте с жидкими металлами при высоких температурах и обеспечение комплекса физико-химических свойств жидкого металла при проведении различных технологических процессов, невозможно без детального учета термодинамических характеристик большого количества систем типа твердый металл – расплав. Решение этих задач требует нахождения различных термодинамических параметров, среди которых активности, растворимости, парциальные давления, параметры взаимодействия между компонентами и т.д. Если для двухкомпонентных систем необходимые термодинамические данные можно получить из литературных источников, то для трех- и многокомпонентных систем такая информация в большинстве случаев отсутствует. Так как задача экспериментального определения термодинамических характеристик для всех представляющих интерес систем является практически невыполнимой, то необходимая информация может быть получена с помощью статистических моделей растворов, позволяющих расчетным путем находить значения термодинамических величин в трех- и четырехкомпонентных системах, используя экспериментальные данные для соответствующих двойных систем. Потребность в развитии теорий и моделей для описания физико-химических характеристик многокомпонентных металлических расплавов связана с появлением новых научно-технических задач, среди которых необходимо отметить следующие:

1.  Разработка концепции самоохлаждаемого литий-литиевого бланкета ТЯР.

2.  Создание конструкционных материалов, совместимых с расплавом литий-свинец эвтектического состава, для жидкометаллических систем энергетических установок.

3.  Развитие направлений материаловедения, связанных с созданием керамических материалов, устойчивых к воздействию жидких металлов, в том числе самовосстанавливающихся электроизоляционных покрытий на поверхности каналов жидкометаллических систем прототипов ТЯР.

4.  Совершенствование технологии извлечения трития из литийсодержащих расплавов, рассматриваемых в качестве перспективных материалов бланкета ТЯР.

Следует отметить, что в последние десятилетия достигнут существенный прогресс в развитии методов статистической термодинамики для описания разбавленных растворов неметаллов в бинарных металлических расплавах. В то же время, модели, описывающие свойства растворов неметаллов в трехкомпонентных металлических растворителях, не могут быть признанными удовлетворительными, как с точки зрения полноты учета различных видов взаимодействия между компонентами расплава, так и вследствие использования необоснованно большого количества вспомогательных параметров, нахождение которых является достаточно трудоемкой задачей.

Цель работы – развитие кластерных моделей статистической термодинамики для расчета физико-химических характеристик металлических расплавов, содержащих неметаллические компоненты, и для прогнозирования процессов на границе раздела твердый металл – расплав.

Осуществление поставленной цели потребовало решения следующих конкретных задач:

1. Установление связи между термодинамическими характеристиками четырехкомпонентного металлического расплава и его кластерным составом.

2. Проведение расчетно-теоретической оценки влияния добавок четвертого компонента на термодинамические характеристики трития в расплавах системы литий – свинец.

3. Расчетно-теоретическое и экспериментальное обоснование метода прогнозирования направления изотермического переноса массы в расплавах, содержащих неметаллические примеси.

4. Разработка метода расчета равновесной концентрации неметаллического компонента керамического материала в бинарном металлическом расплаве для определения областей температур и составов жидкой фазы, где рассматриваемый материал и расплав совместимы друг с другом.

Научная новизна. В ходе выполнения диссертационной работы были впервые получены следующие результаты:

·  Разработана обобщенная координационно-кластерная модель для описания взаимодействий и расчета термодинамических характеристик раствора неметалла в расплаве из трех металлических компонентов.

·  Установлена связь между термодинамическими свойствами (коэффициентами термодинамической активности и параметрами взаимодействия компонентов первого порядка) и локальным упорядочением в четырехкомпонентном расплаве для разных типов взаимодействия между металлическими компонентами растворителя (идеальный раствор, положительные и отрицательные отклонения от идеальности).

·  Разработан метод оценки влияния небольших (менее 0,5 % ат.) добавок металлических компонентов на термодинамическую активность трития в жидком литии и расплавах системы литий-свинец. Установлено, что в диапазоне 400-800оС наиболее эффективной с точки зрения снижения термодинамической активности трития в жидком литии и расплаве Li17Pb83 является добавка иттрия.

·  Показано, что небольшие (менее 0,5 % ат.) добавки лантана и иттрия в расплавы системы свинец-литий-тритий смещают концентрационную границу, разделяющую расплавы с отрицательными и положительными отклонениями от идеальности, в область более высоких содержаний свинца. Установлено, что в присутствии иттрия в этом же направлении происходит изменение пороговой концентрации свинца, при которой реакция растворения трития в расплаве из экзотермической становится эндотермической.

·  Сформулирован метод расчета равновесного коэффициента распределения металлоида между твердой фазой и двухкомпонентным металлическим расплавом, учитывающий зависимость коэффициента распределения от всех парных энергий взаимообмена между компонентами четверной системы. Показано, что использование полученных уравнений позволяет устранить наблюдаемое в ряде систем несоответствие экспериментальных и расчетных величин коэффициента распределения.

·  В результате исследования изотермического переноса массы в системах Fe–Ni–Na–O, Fe–Nb–Na–O и Fe–Mo–Na–O при 800ºС показана применимость уравнений координационно-кластерной модели для прогнозирования коррозионных процессов в жидких металлах в присутствии неметаллических примесей. Установлена корреляция между величинами параметров взаимодействия первого порядка в жидкой фазе атомов растворяющегося твердого металла с атомами неметалла и направлением преимущественного переноса массы в гетерогенной системе. Преимущественный перенос массы в статических изотермических условиях происходит от металла с наибольшим значением параметра взаимодействия к металлу, у которого абсолютное значение этого параметра меньше.

·  Разработан метод расчета равновесной концентрации неметаллического компонента керамического материала в бинарном металлическом расплаве, позволяющий определять области температур и составов жидкой фазы, где рассматриваемый материал и расплав совместимы друг с другом.

Практическая значимость работы. Обобщенная координационно-кластерная модель для описания взаимодействий и расчета термодинамических характеристик раствора элемента внедрения в трехкомпонентном металлическом расплаве уже проявила свою эффективность при интерпретации экспериментальных данных для широкого круга систем и процессов, протекающих в расплавах и гетерогенных системах с участием жидкой фазы.

Результаты расчетно-теоретического исследования термодинамики растворов трития в жидком литии и расплавах, содержащих литий, могут быть использованы для совершенствования методов контроля содержания трития в бланкете и оптимизации процессов извлечения трития из жидкометаллического бланкета в разрабатываемых прототипах энергетического термоядерного реактора.

Практически важным, с точки зрения выбора конструкционных материалов жидкометаллических систем энергетических установок, является метод прогнозирования направления преимущественного переноса массы в гетерогенной системе с помощью параметров взаимодействия между компонентами в многокомпонентном расплаве.

Метод расчета равновесной концентрации неметаллического компонента керамического материала в бинарном металлическом расплаве, основанный на использовании уравнений обобщенной координационно-кластерной модели, позволяет в значительной степени сократить объем экспериментальных исследований по оценке совместимости рассматриваемого материала с металлическим расплавом.

Основные положения, выносимые на защиту.

1. Обобщенная координационно-кластерная модель для описания взаимодействий и расчета термодинамических характеристик раствора неметалла в расплаве из трех металлических компонентов.

2. Результаты расчетно-теоретической оценки влияния добавок четвертого компонента на термодинамические характеристики трития в расплавах системы литий – свинец.

3. Метод прогнозирования направления изотермического переноса массы в статических условиях в расплавах, содержащих неметаллические примеси.

4. Метод расчета равновесной концентрации неметаллического компонента керамического материала в бинарном металлическом расплаве, позволяющий определять области температур и составов жидкой фазы, где рассматриваемый материал и расплав совместимы друг с другом.

5. Метод расчета поверхностного натяжения и состава поверхности бинарных металлических расплавов с помощью уравнений квазихимической модели, позволяющий учесть существование ближнего упорядочения в объеме и на поверхности расплавов.

Апробация работы. Основные результаты диссертации докладывались на III Всесоюзной конференции по исследованию и разработке конструкционных материалов для реакторов термоядерного синтеза (Ленинград, 1984 г.), 2-ой международной конференции "Радиационное воздействие на материалы термоядерных реакторов" (СПб, 1992 г.), международной конференции Liquid Metalal Systems – Material Behavior and Physical Chemistry in Liquid Metalal Systems II, March 16-18, 1993, Karlsruhe, Germany, 5-ой международной конференции Tritium Technology in Fission, Fusion and Isotopic Applications, 28 May–3 June 1995, Lake Maggiore, Italy, 8-ой международной конференции Eight International Conference on Fussion Reactor Materials, October 26–31,1997, Sendai, Japan, 6-ой международной конференции 6th International Conference on Tritium Science and Technology, November 11-16, 2001, Tsukuba, Japan и научно-практической интернет-конференции "Техника, технология и перспективные материалы" (Москва, 2002 г.).

Публикации. По основным результатам диссертации опубликовано 27 работ.

Объем и структура работы. Диссертация состоит из введения, шести глав, заключения, списка литературы из 214 наименований, содержит 67 рисунков и 52 таблицы. Общий объем диссертации составляет 290 страниц машинописного текста.

Обобщенная координационно-кластерная модель для

 описания четырехкомпонентных систем

Известно, что в жидких и твердых телах при температурах, близких к температуре плавления, межатомные расстояния и координационные числа отличаются несущественно. Это позволяет и в случае металлических расплавов при обсуждении типов упаковки атомов в жидкости говорить о существовании октаэдрических и тетраэдрических пустот в разупорядоченных (т. е. не обладающих дальним порядком) структурах. Если для твердых растворов металлоидов эти пустоты принято называть позициями внедрения, то при описании структуры жидкостей[1] и аморфных тел чаще применяется термин “квазимеждоузлия”.

Приступая к рассмотрению разбавленных растворов неметаллов в расплавах, содержащих три металлических компонента, необходимо отметить, что все энергетические эффекты, сопровождающие процесс растворения атома металлоида в расплаве, можно отнести к трем типам:

1. Связанные с взаимодействием растворенного атома (неметалла) с соседними атомами растворителя.

2. Обусловленные взаимодействием между соседними атомами растворителя, находящимися в первой координационной сфере вокруг атома металлоида.

3. Связанные с неэквивалентностью энергетических состояний

атомов растворителя, находящихся в первой координационной сфере вокруг атома неметалла, и атомов этого же элемента, находящихся в “объеме” расплава (т. е. вне первой координационной сферы вокруг атома металлоида).

В дальнейшем предполагается, что атомы неметалла А4 в жидком разбавленном растворе трех металлов А1, А2 и А3 занимают “квазимеждоузлия” с координационным числом z. Каждый атом А4 в растворе в качестве ближайших соседей имеет j атомов А1, k атомов А2 и l атомов А3 . В растворе существует (z+1)(z+2)/2 видов таких конфигураций, которые называются кластерами и обозначаются . При этом надо учитывать, что в расплаве атомы находятся в непрерывном движении, так что имеет смысл говорить об усредненной в течение некоторого времени[2] t конфигурации атомов.

В расплаве можно выделить две области. Первая область, которую обозначим “B”, содержит все металлические атомы, не имеющие в качестве ближайших соседей атомов А4. При рассмотрении разбавленных растворов металлоидов, в область “B” попадает большая часть атомов расплава. Вторая область, которую обозначим “C”, состоит из атомов А1, А2 и А3, которые в качестве ближайших соседей имеют атомы А4. Очевидно, атомы металлоида также входят в область “C”.

Если рассматривать расплавы системы А1 - А2 - А3 - А4 с различным содержанием компонентов, то в расплаве произвольного состава при данной температуре будет устанавливаться строго определенное равновесное распределение атомов А4 по кластерам, которое может быть охарактеризовано набором некоторых величин cj,k , где каждая из cj,k есть ни что иное, как доля атомов компонента А4, находящихся в конфигурации .

При изменении температуры (или состава) в расплаве устанавливается новое равновесное распределение cj,k. В этом случае процесс перехода расплава в новое положение равновесия можно представить в виде набора уравнений реакций следующего вида (количество уравнений кратно числу различных типов кластеров в системе):

 + А2(“B”) =  + А1(“B”)

 + А3(“B”) =  + А3(“B”)    (1)

Для коэффициента термодинамической активности металлоида в разбавленном в растворе из трех металлических компонентов получено следующее уравнение

,       (2)

где  – коэффициент термодинамической активности A4 в четырехкомпонентном расплаве; γ1(1-2-3), γ2(1-2-3), γ3(1-2-3) – коэффициенты термодинамической активности компонентов тройной системы А1–А2–А3 ; γ4(1), γ4(2), γ4(3) – коэффициенты термодинамической активности А4 в двойных расплавах А1–А4, А2–А4 и А3–А4 соответственно;  – сочетания из z элементов по j ; x1, x2, x3 – мольные доли металлических компонентов в четырехкомпонентном расплаве; h12 , h23 и h13 – энергетические параметры (константы для тройных систем А1–А2–А4, А2–А3–А4 и А1–А3–А4 при каждой температуре), учитывающие нелинейный характер зависимости смещения электронной плотности между компонентами кластера от его состава; t – параметр, принимающий значения в пределах от 0,25 до 0,5 и учитывающий ослабление связей типа металл-металл для атомов, находящихся в первой координационной сфере вокруг атома А4.

Для концентраций кластеров различного типа получены следующие уравнения в котором количество слагаемых совпадает с количеством типов кластеров, различного состава и равно (z+1)(z+2)/2.

,               (3)

где j = 0,1,…z; k = 0,1,…z; j+k ≤ z .

Очевидно, должно выполняться соотношение

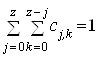 ,                            (4)

Необходимо сделать некоторые замечания, относящиеся к определенной группе четырехкомпонентных расплавов. Если в системе А1–А2–А3–А4 концентрации компонентов A1 и A2 могут изменяться в широких пределах, а концентрации A3 и A4 не превышают 1-2 % ат., то влияние третьего металлического компонента на термодинамическую активность металлоида A4 в расплаве удобно оценивать с помощью удельного параметра взаимодействия σ34, который определяется следующим образом

 ,

или с учетом (2),

,    (5)

где  - коэффициент активности А3 в тройном расплаве А1-A2-A3 при x3®0.

Для физической интерпретации модели в случае четырехкомпонентной системы А1-А2-А3-А4 проанализировано влияние характера взаимодействия[3] между металлическими компонентами на кластерный состав расплава и термодинамические характеристики растворенного металлоида А4. Расчеты, проведенные для ряда модельных четырехкомпонентных систем, отличающихся по характеру взаимодействия между компонентами, показали, что в расплаве из четырех компонентов между атомами различных элементов наблюдается своеобразная “конкуренция”. В частности, при сильном взаимодействии между атомами А1 и А2 (отрицательные отклонения от идеального раствора) атомы элементов А1 и А2 менее "активно" участвуют в образовании кластеров с центральным атомом А4, что приводит к увеличению концентрации кластеров, в которых атом А4 связан с атомами А3 (рис. 1, 2), и наоборот.

Результаты расчета термодинамических характеристик для расплавов Fe-Ni-Co-N и Ag-Cu-Sn-O во всем диапазоне концентраций металлических компонентов по уравнениям обобщенной координационно-кластерной модели (ОККМ) согласуются с экспериментальными данными (рис. 3, 4), полученными в работах У.Блока ( Block U., Stuve H.P. – Z. Metallkunde. - 1969. - Bd. 74. - S.709) и Р.Пелка ( Blossey R.G., Pehlke R.D. –Transactions of the metallurgical society of AIME. - 1966. - V. 236. - № 4. - P. 566).

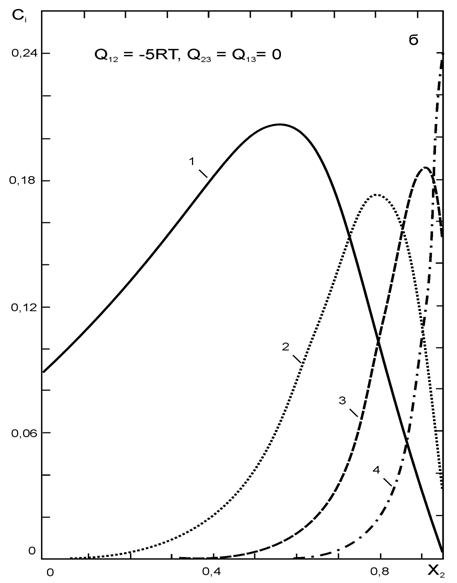
Рис. 1. Зависимость доли атомов А4, находящихся в конфигурации A4[(A1)j(A2)k(A3)l], от содержания А2 в расплавах, насыщенных компонентом А4, при х3=0,01 (h12=h23=h13=0) :

1 -  А4 [(А1)3(А2)0(A3)1];           2 -   А4 [(А1)2(А2)1(A3)1];

3 -  А4 [(А1)1(А2)2(A3)1];           4 -   А4[(А1)0(А2)3(A3)1]

( Q12 - энергия взаимообмена в двойной системе A1-A2 в приближении регулярных растворов )

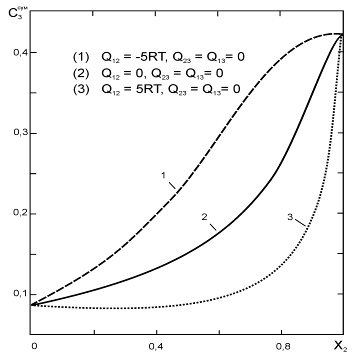
Рис. 2. Зависимость доли атомов А4, находящихся в кластерах всех типов с атомами А3, от содержания компонента А2 в расплавах, насыщенных компонентом А4, при х3=0,01 (h12=h23=h13=0)

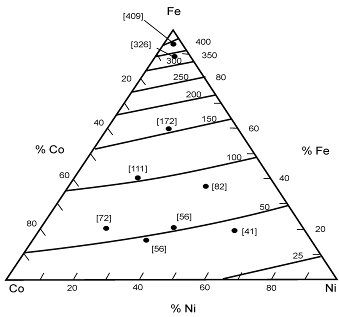
Рис. 3. Растворимость азота С (10-4%) в расплавах Fe-Ni–Co
при 1600оС и давлении 1 атм

¾     - эксперимент (Р.Пелк );

[  ]    - расчет по уравнениям ОККМ

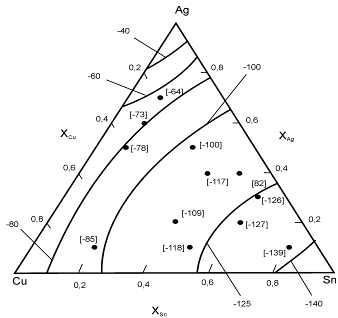
Рис. 4. Энергия Гиббса (кДж/моль) растворения кислорода в
 расплавах Ag-Cu-Sn при 1200оС и давлении 1 атм
(стандартное состояние: 1ат.% кислорода).

¾     - эксперимент (У.Блок );

[  ]    - расчет по уравнениям ОККМ

Прогнозирование изменения термодинамической активности

 изотопов водорода в жидком литии и Li17Pb83

в присутствии металлических примесей

Уравнения ОККМ использовались для оценки влияния небольших (менее 0,5 ат.%) добавок третьего компонента на термодинамическую активность изотопов водорода в жидком литии. Расчеты, проведенные для систем Li – T – Al, Li – T – Mg, Li – T – Si, Li – T – La и Li – T – Y, показали, что добавки алюминия, магния и кремния практически не влияют на термодинамическую активность трития в литии при температурах 400-800ОС. В то же время добавки иттрия и лантана в значительной степени снижают термодинамическую активность трития. Влияние иттрия проявляется сильнее при температурах ниже 500ОС.

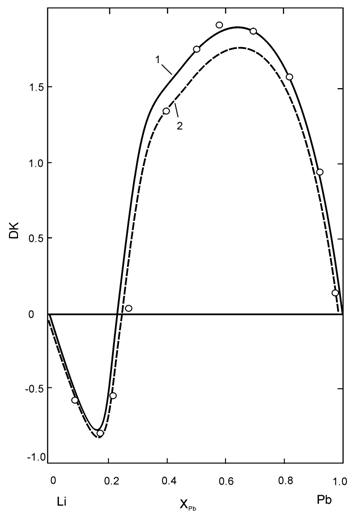
Для расплавов системы литий – свинец при концентрациях близких к эвтектической Li17Pb83 добавки иттрия являются самыми эффективными с точки зрения снижения термодинамической активности трития. Расчеты, проведенные для всего диапазона концентраций двойной системы литий – свинец, показали, что небольшие (менее 0,5 ат.%) количества иттрия смещают концентрационную границу, разделяющую расплавы с отрицательными и положительными отклонениями от идеальности в область более высоких содержаний свинца (рис. 5). Используя зависимость производной коэффициента термодинамической активности трития по температуре от содержания иттрия в расплаве, было установлено, что добавка иттрия изменяет пороговую концентрацию, при которой реакция растворения трития в расплаве литий – свинец из экзотермической становится эндотермической.

Из расчетов удельного параметра взаимодействия иттрий – тритий, проведенных для различных содержаний свинца в расплавах системы Li-Pb-Y-Т, следует что добавка иттрия в максимальной степени снижает коэффициент термодинамической активности трития в расплавах, для которых 0,3<xPb<0,8 (xPb –мольная доля свинца в расплаве). Исследование

Рис. 5. Влияние содержания свинца на величину DK для растворов трития в бинарных расплавах Li-Pb (1) и в расплавах Li-Pb, содержащих 0,1 ат.% Y (2), при 659оС:

(1) и (2)  - расчет по уравнениям ОККМ ;

○       - экспериментальные данные для двойной системы Li-Pb

(Chan Y.C., Veleckis E. – J. Nucl. Mater., 1984. - V. 122-123.- P.935)

зависимости кластерного состава расплавов этой системы от температуры показало, что для расплава по составу близкого к эвтектическому доля атомов трития, находящихся в кластерах всех типов, содержащих иттрий, максимальна при температурах 450-500ОС.

Уравнения, полученные на основе координационно-кластерной модели четырехкомпонентных расплавов, позволяют не только находить величины коэффициентов термодинамической активности неметаллического компонента (трития), но и определять положение критических точек, где расплав меняет характер отклонения от идеальности, а также точек, где реакция растворения элемента внедрения из экзотермической становится эндотермической.

Для расчета равновесного коэффициента распределения элемента внедрения между твердой фазой и двухкомпонентным металлическим расплавом получены уравнения, в которых учтено, что коэффициент распределения является функцией всех парных энергий взаимообмена между компонентами четверной системы. На примере системы иттрий – литий – свинец – водород показано, что учет взаимодействия между атомами иттрия и водорода в жидкой фазе приводит к более низким значениям коэффициента распределения водорода, чем те, которые получаются в результате стандартных расчетов. Это позволяет объяснить наблюдаемое в ряде систем несоответствие экспериментальных и расчетных величин коэффициента распределения.

Взаимодействие металлических конструкционных материалов с жидкими металлами, содержащими неметаллические примеси

При рассмотрении возможности применения жидкого металла или расплава основным критерием его совместимости с конструкционным материалом может быть величина равновесной растворимости компонентов последнего в жидкой фазе. Однако вследствие несовершенства методов определения малых величин растворимостей, более достоверные данные о влиянии неметаллических примесей на совместимость жидкого металла (расплава) с конструкционным материалом во многих случаях удается получить из результатов исследования переноса массы в гетерогенных условиях.

Известно, что при изотермическом переносе массы в системе из двух чистых металлов (в твердом состоянии), разделенных жидкометаллическим расплавом, изменение массы единицы поверхности каждого из них является функцией растворимостей как первого, так и второго металлов в жидкой фазе[4].

В результате экспериментального исследования массопереноса в жидком натрии установлена корреляция между величинами параметров взаимодействия первого порядка атомов растворяющегося твердого металла с атомами неметаллического элемента в жидкой фазе и направлением преимущественного переноса массы в гетерогенной системе. Если расположить металлы (твердые в рассматриваемом диапазоне температур), являющиеся компонентами гетерогенных систем Fe-Ni-Na-O, Fe-Nb-Na-O и Fe-Mo-Na-O, в порядке возрастания абсолютных значений параметра взаимодействия с кислородом в разбавленных растворах на основе натрия при 800ОС, то получается следующий ряд: Ni, Mo, Fe, Nb. Проведенные эксперименты показали, что в исследованных системах преимущественный перенос массы происходит от металла с наибольшим значением параметра взаимодействия к металлу, у которого абсолютное значение этого параметра меньше. Сравнение рассчитанных величин параметров взаимодействия первого порядка с экспериментальными данными, имеющимися в литературе, показывает, что установленная закономерность справедлива и для систем на основе лития, в которых в качестве примеси присутствует азот.

Результаты расчета параметров взаимодействия первого порядка в разбавленных растворах систем натрий – ниобий – кислород и калий – ниобий – кислород согласуются с величинами определенными экспериментально. Системы Na-Nb-O и K-Nb-O относятся именно к той группе систем, где за счет сильного взаимодействия между атомами кислорода и ниобия, расчеты по стандартной методике приводят к существенно завышенным значениям коэффициента распределения кислорода между ниобием и жидким щелочным металлом по сравнению экспериментальными величинами. Расчет с использованием уравнений координационно-кластерной модели для трехкомпонентных растворов позволяет преодолеть это несоответствие.

Из анализа результатов расчета и имеющихся экспериментальных данных по определению растворимости ниобия в жидком калии следует, что в системе K-Nb-О при 600ОС образования двойного оксида ниобия и калия не происходит, по крайней мере, до концентрации 0,22% кислорода в калии.

Полученные в результате расчетов большие по абсолютной вели-чине отрицательные значения параметров взаимодействия с азотом в системах Li-Fe-N, Li-Cr-N и Li-Mo-N качественно подтверждаются имеющимися экспериментальными данными по влиянию примеси азота на совместимость железа, хрома и молибдена с жидким литием. Величины пороговой концентрации образования тройного соединения лития с хромом и азотом свидетельствуют о том, что образование Li9CrN5 необходимо учитывать при рассмотрении условий равновесия в системах, где присутствуют литий, хром и азот. Из уравнений модели также следует, что растворимость никеля в литии при температурах 300-900ОС практически не зависит от содержания азота в жидком металле. В системах на основе лития, где неметаллическим компонентом является водород, параметры взаимодействия принимают существенно меньшие по абсолютной величине значения, чем в системах, состоящих из тех же металлических компонентов, но с азотом в качестве элемента внедрения. Это свидетельствует о более слабом влиянии водорода на растворимость металлов в литии. Если расположить твердые металлы, являющиеся компонентами систем Li-Ni-H, Li-Nb-H, Li-V-H, Li-Cr-H и Li-Fe-H, в порядке возрастания абсолютных значений параметра взаимодействия с водородом при 550ОС, то получим следующий ряд: Ni, Cr, Fe, V, Nb.

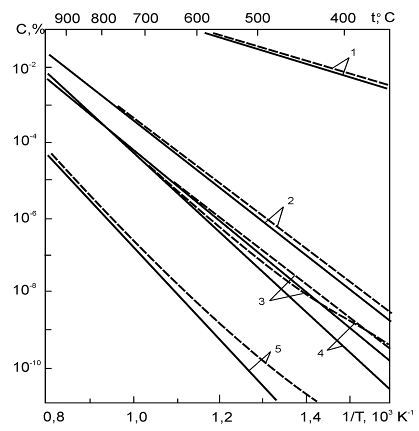
Рис. 6. Температурная зависимость растворимости никеля (1), хрома (2), ванадия (3), железа (4) и ниобия (5) в чистом литии и литии с 0,05% водорода (- - - -)

Проведенные расчеты показали (рис. 6), что влияние примеси водорода на растворимость металлов в литии могло бы проявиться только в области относительно низких температур, где абсолютные значения растворимости чрезвычайно низки. В то же время имеющиеся данные свидетельствуют о том, что примесь водорода в литии может существенно влиять на процессы перераспределения других примесей внедрения (азот, углерод) в гетерогенных системах.

Совместимость металлических материалов с двухкомпонентными
металлическими расплавами

Известно, что совместимость конструкционного материала с металлическим расплавом в значительной степени зависит от величин равновесной растворимости компонентов этого материала в жидкой фазе. Если для жидких легкоплавких металлов (Na, K, Li) имеются экспериментальные данные, позволяющие оценить их совместимость с конструкционными материалами различных классов, то для двухкомпонентных расплавов (Li-Pb и др.), применение которых возможно, необходимые сведения в большинстве случаев отсутствуют. Дополнительные затруднения возникают при наличии в расплавах неметаллических примесей – кислорода, азота, водорода, которые сильно влияют на совместимость жидких и твердых металлов. Для предварительной оценки совместимости конструкционных материалов с многокомпонентными расплавами в настоящей работе предложена методика расчета растворимости твердых металлов в чистых двухкомпонентных расплавах, а также в расплавах, содержащих неметаллические примеси.

Используя разложение в ряд Тейлора избыточной парциальной мольной энергии Гиббса третьего компонента, получено выражение, позволяющее учесть в первом приближении влияние неметаллической примеси в расплаве[5] на растворимость твердого металла А3 в жидкой фазе:

 ,                   (6)

где  – растворимость А3 в расплаве, содержащем x4 мольных долей неметаллического компонента;  – растворимость А3 в расплаве того же состава, но не содержащем примесей неметаллов; – удельный параметр взаимодействия. Следует отметить, что уравнение (6) справедливо только для систем, в которых компоненты А1 и А2 не образуют твердых растворов с А3.

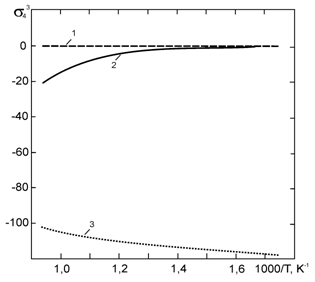
Рис. 7. Температурные зависимости удельных параметров взаимодействия ,  и  в системах Li-Pb-Ni-O,

Li-Pb-Fe-O и Li-Pb-Cr-O вблизи состава хLi=0,17 и xPb=0,83

Расчеты, проведенные для расплавов эвтектического состава Li17Pb83, находящихся в контакте с хромом, никелем и железом, показали (рис. 7), что в гетерогенных системах наибольшее влияние примесь кислорода должна оказывать на перенос хрома между материалами и практически не оказывать никакого эффекта на растворение и перенос никеля в расплаве.

Такие результаты находятся в соответствии с экспериментальными наблюдениями (T.Flament, P.Tortorerelli, V.Coen, H.U.Borgstedt – J. Nucl. Mater. - 1992. - V.191-194. – Part A. - P. 132) . Учитывая очень низкую растворимость кислорода в расплаве Li17Pb83 (менее 1·10-4 % ат. при 550ОС), более обоснованным можно считать коррозионный механизм, который предполагает сильную зависимость константы скорости растворения хрома от содержания кислорода в расплаве. Основываясь на имеющихся экспериментальных данных, нельзя исключить возможности того, что промежуточной ступенью, контролирующей скорость растворения твердого металла в расплаве, является образование тройного соединения хрома с литием и кислородом на начальной стадии процесса.

Выбор эвтектического расплава Na-K был обусловлен наличием большого, по сравнению с другими двухкомпонентными расплавами, накопленного экспериментального материала по исследованию его совместимости с твердыми металлами. В двойном эвтектическом расплаве натрий – калий расчеты по уравнениям ОККМ привели к большим величинам удельного параметра взаимодействия между атомами хрома и кислорода в жидкой фазе, что свидетельствует о сильной зависимости растворимости хрома в расплаве натрий – калий от содержания неметаллической примеси. Примесь кислорода в жидкой фазе практически не оказывает влияния на растворимость и перенос чистого никеля в расплаве (в отличие от Fe и Cr). В целом, расчеты подтвердили, что по степени влияния кислорода на растворимость компонентов конструкционных материалов натрий – калиевый сплав близок к натрию.

Совместимость керамических материалов с двухкомпонентными
металлическими расплавами

При рассмотрении возможности применения керамического материала в условиях, когда последний находится в контакте с жидким металлом или его парами, удобным критерием является равновесная концентрация неметаллического компонента в жидком металле, при которой химическое соединение стабильно в среде жидкого металла.

Для предварительной оценки совместимости керамических материалов с двухкомпонентными металлическими расплавами в настоящей работе предлагается методика расчета равновесной концентрации неметаллического компонента во всем концентрационном диапазоне бинарной системы.

Рассматривая термодинамическое равновесие между химическим соединением АmBn и жидкометаллическим расплавом, содержащим хLi мольных долей лития и хPb мольных долей свинца, было получено следующее выражение для расчета равновесной концентрации компонента В в расплаве

 .               (7)

Вычисления  проводились в приближении субрегулярных растворов для трехкомпонентных систем, используя следующее уравнение

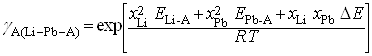 ,         (8)

где gA(Li-Pb-A) – коэффициент активности металлического компонента А в трехкомпонентной системе Li-Pb-A; хLi и хPb – мольные доли лития и свинца в трехкомпонентной системе Li-Pb-A; DЕ = ЕLi-A + EPb–A – ELi-Pb; ЕLi-A , ELi-B и ELi-Pb – энергии взаимообмена для соответствующих пар атомов в бинарных системах (для ELi-Pb учитывалась зависимость от состава расплава). Вычисления значений коэффициента активности неметаллического компонента В в системе Li – Pb – B проводились по уравнениям координационно-кластерной модели для трехкомпонентных расплавов.

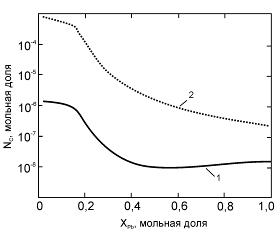
Результаты расчета для системы SiC – расплав Li17Pb83 (рис. 8) показали, что при температурах, не превышающих 1150 К, равновесная концентрация углерода для SiC ниже концентрации насыщения углерода в расплаве. Это означает, что при содержаниях углерода, превышающих пороговое (выше сплошной кривой), соединение SiC должно быть стабильным в Li17Pb83 при этих температурах. При температуре 932 К существует область концентраций углерода в жидкой фазе, где соединение SiC является стабильным во всем концентрационном интервале двойной системы Li–Pb (рис. 9).

С помощью уравнений координационно-кластерной модели проанализировано влияние температуры на характер межатомных взаимодействия в расплавах Li-Pb. Модель позволяет оценивать долю атомов сi углерода, находящихся в кластерах определенного состава С(Lij Pbk Sil). Вероятности различных кластеров рассчитывались при очень низкой концентрации кремния в расплаве (хSi = 10-10 мольн. долей), которая близка к равновесной для соединения SiC при температурах 800-900 К. Как следует из результатов расчета, доля межатомных связей типа литий-углерод возрастает с понижением температуры расплава эвтектического состава. Вероятность образования кластеров различного состава, содержащих атом кремния в первой координационной сфере атома углерода, также возрастает при низких температурах расплава (рис. 10). Величины удельного параметра взаимодействия  с понижением температуры изменяются аналогичным образом. Равновесная концентрация углерода для соединения SiC растет с повышением температуры, что свидетельствует о снижении термодинамической стабильности этого соединения в расплавах. Таким образом, наблюдается корреляция между равновесной концентрацией углерода в жидком металле для системы SiC - расплав Li-Pb и количеством парных связей между атомами углерода и кремния в этом расплаве.

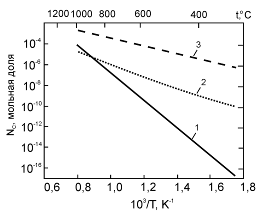
Рис. 8. Температурная зависимость минимальной концентрации
углерода NС в расплаве Li17Pb83, необходимой для образования SiC;
1 – концентрация, соответствующая равновесию SiC – Li17Pb83;
2 – концентрация насыщения углерода в Li17Pb83, рассчитанная по уравнению ОККМ; 3 – концентрация насыщения углерода в Li17Pb83, рассчитанная по модели идеальных растворов

Рис. 9. Зависимость минимальной концентрации углерода, необходимой для образования SiC от состава для двойной системы Li-Pb при 932К;
1 – концентрация, соответствующая равновесию SiC– расплав;
2 – концентрация насыщения углерода в расплаве, рассчитанная по уравнению ОККМ.

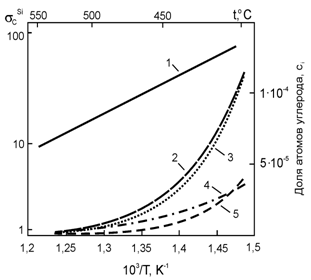
Рис. 10. Зависимость удельного параметра взаимодействия и доли атомов углерода ci , находящихся в конфигурации С(Lij Pbk Sil), от температуры для расплава Li17Pb83, содержащего хSi=10-10 мольных долей:
1 -  ; 2 – сi для С(Li1Pb2Sil); 3 - сi для С(Li2Pb1Si1); 4 - сi для С(Li0Pb3Sil); 5 - сi для С(Li3Pb0Sil)

Имеющиеся в литературе экспериментальные данные о коррозионной стойкости карбида кремния в чистом литии свидетельствуют о том, что это соединение разлагается в жидком металле при температуре выше 900ОС (Ghoniem N.M. – J. Nucl. Mater. - 1992.- V.191-194.- Part A. - P. 515). Таким образом, можно констатировать удовлетворительное согласие результатов расчета с экспериментальными данными.

Применение методов статистической термодинамики

 к металлическим системам, компоненты которых образуют

диаграммы состояния с расслоением в жидкой фазе

Известно, что существуют значительные различия между обычными диаграммами состояния, отражающими условия равновесия достаточно больших объемов существующих фаз, и диаграммами состояния для систем, состоящих из высокодисперсных частиц. Причиной смещения межфазных границ является влияние на фазовые равновесия поверхностной энергии, которая вносит существенный вклад только в том случае, если размер частиц по порядку величины не превосходит некоторого порогового значения (не более нескольких микрометров).

В работе предложена методика расчета поверхностного натяжения и состава поверхности бинарных металлических расплавов с помощью уравнений квазихимической модели, позволяющая учесть существование ближнего упорядочения в объеме и на поверхности расплавов. Показано, что использование этой модели позволяет предсказывать возможные направления изменения формы изотерм поверхностного натяжения и зависимостей состава поверхности от состава расплава в системах с отрицательными отклонениями от идеальности. Проведено сравнение полученных зависимостей с результатами расчета по моделям регулярных и совершенных растворов и экспериментальными данными для систем никель – кремний и медь – алюминий.

Проведено расчетно-теоретическое исследование влияния дисперсности частиц расплава на критическую температуру расслоения в системах из несмешивающихся компонентов. Причиной смещения межфазных границ является влияние на фазовые равновесия поверхностной энергии, которая вносит существенный вклад только в том случае, если размер частиц по порядку величины не превосходит некоторого порогового значения.

На основании термодинамических оценок показано, что в двухкомпонентных системах с расслоением в жидком состоянии (в случае, когда размер частиц расплава не превышает нескольких микрометров) следует ожидать смещения границы раздела между областью однородного расплава и двухфазной областью в сторону более низких температур по сравнению с обычными диаграммами состояния. Установлено, что снижение верхней критической температуры расслоения происходит тем значительнее, чем выше степень дисперсности частиц расплава. Расчеты проведены для трех двухкомпонентных систем: алюминий – индий, медь – свинец и медь – хром.

При использовании математического подхода, предложенного ранее для оценки скорости растворения сферической частицы в неограниченной матрице, проведены расчеты кинетических параметров процесса взаимодействия расплава легкоплавкого металла А3 с двухфазной композицией, один из компонентов которой образует вместе с А3 диаграмму состояния с расслоением в жидком состоянии. Отмечено хорошее соответствие между результатами расчета и экспериментальными данными для системы Fe-Cu - расплав свинца.

1. Разработана обобщенная координационно-кластерная модель для описания взаимодействий и расчета термодинамических характеристик раствора неметалла в расплаве из трех металлических компонентов. Установлена связь термодинамических характеристик компонентов с относительной концентрацией кластеров различного состава и свойствами растворителя.

2. Сформулирован метод оценки влияния небольших (менее 0,5 % ат.) добавок металлических компонентов на термодинамическую активность трития в жидком литии и расплавах системы литий-свинец. Установлено, что в диапазоне 400-800оС наиболее эффективной с точки зрения снижения термодинамической активности трития в жидком литии и расплаве Li17Pb83 является добавка иттрия. Показано, что небольшие (менее 0,5 % ат.) добавки лантана и иттрия в расплавы системы свинец-литий-тритий смещают концентрационную границу, разделяющую расплавы с отрицательными и положительными отклонениями от идеальности в область более высоких содержаний свинца. Установлено, что в присутствии иттрия в этом же направлении происходит изменение пороговой концентрации свинца, при которой реакция растворения трития в расплаве из экзотермической становится эндотермической.

3. Установлена корреляция между величинами параметров взаимодействия первого порядка в жидкой фазе атомов растворяющегося твердого металла с атомами неметалла и направлением преимущественного переноса массы в гетерогенной системе. Преимущественный перенос массы в статических изотермических условиях происходит от металла с наибольшим значением параметра взаимодействия к металлу, у которого абсолютное значение этого параметра меньше. Получены уравнения для расчета растворимости твердого металла в двухкомпонентном металлическом расплаве в присутствии неметаллической примеси. Показана применимость полученных уравнений для оценки совместимости металлических материалов с двухкомпонентными расплавами.

4. Разработан метод расчета равновесной концентрации неметаллического компонента керамического материала в бинарном металлическом расплаве, позволяющий определять области температур и составов жидкой фазы, где рассматриваемый материал и расплав совместимы друг с другом.

5. Разработана методика расчета поверхностного натяжения и состава поверхности бинарных металлических расплавов с использованием квазихимической модели растворов, позволяющая учесть существование ближнего упорядочения в объеме и на поверхности расплавов. Показано, что развитый в диссертации теоретический подход позволяет предсказывать возможные направления изменения формы изотерм поверхностного натяжения и зависимостей состава поверхности от состава расплава в системах с отрицательными отклонениями от идеальности.

Результаты диссертации опубликованы в следующих работах:

1.  Иолтуховский А.Г., Красин В.П., Люблинский И.Е. Исследование стойкости 12%-ых хромистых сталей в расплавах натрий – литий // Материалы для атомной техники. М.: Энергоатомиздат, 1983. –
C.14-23.

2.      Бескоровайный Н.М., Иолтуховский А.Г., Красин В.П. Исследование взаимодействия хромоникелевой стали с натрием, литием и натрием с добавкой 1% лития при 650 ºC // Материалы для атомной техники. - М.: Энергоатомиздат, 1983. – C.23-32

3.  Бескоровайный Н.М., Красин В.П., Кириллов В.Б. Применение квазихимической модели для расчета параметров коррозионных процессов в натрии, содержащем примесь кислорода // Физико-химическая механика материалов. – 1984. - Т. 20. - № 5. - С. 26-30.

4.  Бескоровайный Н.М., Красин В.П., Кириллов В.Б. Изучение состояния примесей железа и кислорода в жидком натрии методом электропереноса // Физико-химическая механика материалов. – 1985. -
Т. 21. - № 1. - С. 112-114.

5.  Красин В.П., Иолтуховский А.Г., Люблинский И.Е. Исследование влияния литиевого геттера на коррозионные процессы в жидком натрии // Металлы и сплавы атомной техники. - М.: Энергоатомиздат, 1985. – С. 9-15.

6.  Бескоровайный Н.М., Красин В.П., Кириллов В.Б. Исследование электропереноса примесей кислорода и железа в жидком натрии // Металлы и сплавы для атомной техники. - М.: Энергоатомиздат, 1985. – С. 22-30.

7.  Бескоровайный Н.М., Красин В.П. Применение координационно–кластерной модели для расчета параметров коррозионных процессов в натрии, содержащем примесь кислорода // Металлы и сплавы для атомной техники. - М.: Энергоатомиздат, 1985. - С. 30-35.

8.  Калин Б. А., Люблинский И.Е., Красин В.П. Требования к фазовому составу хромоникелевой аустенитной стали как материалу первой стенки и бланкета ТЯР с литием в качестве теплоносителя и размножителя трития // Физика и химия обработки материалов. – 1987. -
№ 1. – С. 107-110.

9.  Красин В.П., Бескоровайный Н.М., Люблинский И.Е. Термодинамическая модель для прогнозирования коррозионной стойкости конструкционных материалов в жидких литии и натрии, содержащих неметаллические примеси // Физика и химия обработки материалов. – 1987. - № 1. – С. 45-48.

10.  Кириллов В.Б., Красин В.П., Люблинский И.Е. Влияние примесей азота и кислорода в расплавах лития и натрия на растворимость и массоперенос металлов // Журн. физ. химии. – 1988. - Т. 62. - № 12. – С. 3191-3195.

11.  Красин В.П., Люблинский И.Е., Митин Ю.В. Расчет растворимости конструкционных материалов в многокомпонентных металлических расплавах // Журн. физ. химии. – 1990. - Т. 64. - № 5. – С. 1237-1242.

12.  Красин В.П., Митин Ю.В., Кириллов В.Б. Прогнозирование направления изотермического массопереноса в металлических расплавах с помощью параметров взаимодействия // Журн. физ. химии. – 1990. - Т. 64. - № 10. – С. 2772-2776.

13.  Евтихин В.А., Косухин А.Я., Красин В.П. Влияние водорода на растворимость конструкционных материалов бланкета термоядерного реактора в литии // Атомная энергия. – 1990. - Т.69. - Вып. 4. –
С. 238-239.

14.  Красин В.П. Применение статистической модели с двумя подрешетками для анализа взаимодействий в расплавах Na-O-H // Журн. физ. химии. – 1992. - Т. 66. - № 2. – С. 449-453.

15.  Евтихин В.А., Люблинский И.Е., Красин В.П. Оценка совместимости SiC c эвтектикой Li17Pb83 при высоких температурах // Радиационное воздействие на материалы термоядерных реакторов: Тез. докл. Второй международн. конф., СПб, ЦНИИ КМ “Прометей”. 1992. - С.150.

16.  Красин В.П. Использование различных моделей растворов для расчета свойств поверхности бинарных металлических расплавов // Журн. физ. химии. – 1993. - Т. 67. - № 6. – С. 1205-1209.

17.  Красин В.П., Блащук Ю.Н. Влияние дисперсности частиц на критическую температуру расслоения в системах из несмешивающихся компонентов // Журн. физ. химии. – 1993. - Т. 67. - № 11. –
С. 2149-2152.

18.  Красин В.П., Блащук Т.П., Блащук Ю.Н. Использование теоретических оценок при анализе кинетики процесса контактного легирования // Сборник научных трудов сотрудников института. - М.: МАСИ (ВТУЗ-ЗИЛ), 1995. – С. 11-15.

19.  Красин В.П., Блащук Т.П., Блащук Ю.Н. Диффузионная кинетика двухфазного взаимодействия сплава железо-медь с расплавом свинца // Журн. физ. химии. – 1995. - Т. 69. - № 5. – С. 797-801.

20.  Krasin V.P. Application of Solution Models for the Prediction of Corrosion Phenomena in Liquid Metals // Liquid Metal Systems – Material Behavior and Physical Chemistry in Liquid Metal Systems-II / Edited by H.U. Borgstedt and G. Frees. - N.Y.: Plenum Press, 1995. - P.305-309.

21.  Lyublinski I.E., Evtikhin V.A., Krasin V.P. Numerical and Experimental Determination of Metallic Solubilities in Liquid Lithium, Lithium-containing Nonmetallic Impurities, Lead and Lead-Lithium Eutectic // Journal of Nuclear Materials. - 1995. - V.224. - № 3. - P. 288-292.

22.  Lyublinski I.E., Evtikhin V.A., Krasin V.P. The Effect of Solutes on Thermodynamic Activity of Tritium in Liquid Lithium Blanket of Fusion Reactor // Fusion Technology. – 1995. - V.28. - № 3. – P. 1223-1226.

23.  Lyublinski I.E. Evtikhin V.A. Krasin V.P. Electrical Insulating Coatings for Blanket and Divertor Lithium-Vanadium Liquid Metal Systems // Program and Collected Abstracts “Eighth International Conference on Fusion Reactor Materials”. Sendai, Japan. – 1997. – P. 301.

24.  Krasin V.P., Lyublinski I.E. Influence of the Fourth Component on Tritium Behaviour in Li-Pb Melts // Fusion Science and Technology. – 2002. - V.41. -№ 3. – P. 382-385.

25.  Красин В.П. Применение статистических моделей металлических растворов замещения и внедрения для расчета растворимости компонентов конструкционных материалов в многокомпонентных металлических расплавах // Техника, технология и перспективные материалы: Сборник статей научно-практической INTERNET-конференции. – М. МГИУ, 2002. – С. 121-127.

26.  Красин В.П. Расчет равновесной концентрации компонентов керамических покрытий в двухкомпонентных расплавах литий-свинец с использованием координационно-кластерной модели // Журн. физ. химии. – 2003. - Т. 77. - № 1. – С. 127-130.

27.  Красин В.П. Влияние малых добавок лантана на термодинамические характеристики трития в расплавах системы Li – Pb // Журн. физ. химии. – 2003. - Т. 77. - № 6. – С. 1014-1017.

[1] Такой подход, допустим, если не ставить целью изучение динамических свойств расплавов (диффузия и другие явления переноса).

[2] Для кластеров разумная оценка времени усреднения лежит в диапазоне 10-13 с < t < 10-11 с .

[3] Под характером взаимодействия следует понимать степень отклонения от закона
Рауля (отрицательные или положительные).

[4] На характеристики массопереноса также оказывает влияние способность компонентов образовывать друг с другом твердые растворы. Уравнения, описывающие изменение массы единицы поверхности твердых металлов, содержат коэффициенты диффузии компонентов в каждом из твердых растворов.

[5] Здесь рассматривается система, в которой приняты следующие обозначения: А1 и А2 – компоненты бинарного металлического расплава; А3 – контактирующий с расплавом твердый металл; А4 - неметаллический компонент, присутствующий в расплаве А1-А2 в качестве примеси.