Контрольная работа: Сборник задач и расчетно-графических работ по технологии переработки полимеров

Сборник задач и расчетно-графических работ по технологии переработки полимеров

Содержание

1. Формование изделий (1,2,3,4,5,6,7)

2. Характеристики волокнистых наполнителей (8,9,10)

3. Отверждение термореактивных связующих (11,12,13,14,15,16)

4. Физико-химическое взаимодействие между связующим и наполнителем в переходных слоях(17,18,19,20,21,22,23,24,25,26,27,28,29,30)

5. Диффузионные процессы в системе «связующее-наполнитель» (31,32,33,34,35,36,37,38,39,40,41,42,43)

6. Структура и свойства сетчатых полимеров (44,45)

7. Материальные расчеты (46,47)

8. Статистическая обработка результатов измерений (48)

1. Рассчитать массовую скорость m , г / мин истечения расплавленного поликапроамида при линейной скорости формования v=700 м/ мин капроновой нити метрического номера N=10,7 , если плотность капрона ρ=1,14 г/ см3. Рассчитав эффективное сечение нити S,мкм2 по соотношению

S=106 / Nρ , определите условный радиус нити r.

Решение:

Толщина нити в текстах Т=1000/N=93,4 г/1000м

S=≈82000 мкм2=8,2·10-4см2.

Объёмная скорость V истечения расплава V=v·S=7·104cм/мин·8,2·104см2=57,4 см3/мин

Массовая скорость истечения расплава

m=V·ρ=57,4 cм3/мин·1,14 г/см3=65,4 г/мин=1,09·10-3 кг/с

S=πr2; r=√S/π=√82000/3,14=160 мкм

Ответ: m=65,4 г/мин; r=160 мкм

2. Пользуясь законом Пуазейля m=, определить поправку q, характеризующую отклонение реального полимера от ньютоновской жидкости. Принять : m=65,4 г/мин =1,09·10-3кг/с. ∆P=10кгс/см2=1,02·106Па; r=160мкм; ρ=1,14 г/см3; ℓ=1см ; η=8 Па·с

Подсчитать, во сколько раз понизилась вязкость при течении? Какова причина этого явления?

Решение:

Для расчёта величины q из указанного соотношения все входящие в него величины необходимо выразить в единицах системы СИ:

∆P=10кгс/см2=10/9,8 МПа=1,02 МПа=1,02·106Па

r=160 мкм=160·10-6м=1,6·10-4м; ρ=1,14 г/см3=1,14·10-3кг/см3=1140 кг/м3; ℓ=1см=10-2м;

q=;

В начальном состоянии : η1=ηн

В конечном состоянии : η2=ηк=0,0275ηн

Ответ: q=2,75·10-2; вязкость полимера понизилась в 36 раз.

3. Найти показатель степени m в обобщённом законе течения жидкостей σ=η·γm, если при увеличении напряжения σ в 2 раза скорость деформирования γ увеличилась в 12 раз, а вязкость η жидкого полимера понизилась в 5 раз. О каких структурных изменениях в полимере свидетельствует полученное значение m?

Решение

Записываем обобщённый закон течения в начальном и конечном состояниях рассматриваемой системы:

σ1=η1γ1m

2σ1=0,2η1·12mγ1m

Почленно логарифмируем эти соотношения:

ℓgσ1=ℓgη1+mℓgγ1

ℓg2+ℓgσ1=ℓg0,2+ℓgη1+mℓg12+mℓgγ1

и вычитаем одно из другого:

ℓgσ1-ℓg2-ℓgσ1=ℓgη1+mℓgγ1-ℓg0,2-ℓgη1-mℓg12-mℓgγ1

После взаимного уничтожения некоторых слагаемых получаем алгебраическое уравнение:

+ℓg2=+mℓg12+ℓg0,2;откуда m=≈0,92

Ответ: m=0,92; значение m‹1 свидетельствует об уменьшении размера надмолекулярных структур в процессе переработки полимера.

4.Найти напряжение σ, при котором вязкость расплава поликапроамида составляет η=9 Па·с при скорости деформирования γ=0,3 мин-1, если показатель степени в обобщённом законе течения σ=ηγm m=0,92.

Решение:

γ=0,3 мин-1=с-1=0,005 с-1

Применяем обобщённый закон течения:

σ=9·0,0050,92;

ℓgσ=ℓg9+0,92ℓg(5·10-3)=ℓg9+0,92ℓg5-2,760=0,954+0,92·0,699- 2,76=0,954+0,643-2,760=-1,163. Следовательно σ=10-1,163≈0,07 Па

Ответ: σ=0,07 Па

5. Вычислить среднюю массу межузловых цепей в сетчатом полимере, если модуль упругости при растяжении Ер=109 Па. Расчёт проводить по соотношению где Т=393 К, ρ=1200 кг/м3, R=8,31 Дж/моль·К. Каково соотношение между модулями упругости при растяжении и межслоевом сдвиге?

Решение

Полученное среднее значение массы межузловых цепей Мс=12 г/моль соответствует физическим узлам ветвления (перепутывания), поскольку физические сетки значительно более частые, чем химические сетки.

Ответ: Мс=0,012 кг/моль=12 г/моль

6. Вычислить среднюю толщину d прослойки связующего при равномерном распределении однонаправленных элементарных волоконец в материале. В качестве наполнителя используется техническая нить капрон с линейной плотностью Т=90.Масса прессованного образца 40 г при массовом соотношении связующего и наполнителя 1:1. Плотность эпоксидного связующего ρсв.=1,2 г/см3, плотность капрона ρкапр =1,14 г/см3.Для расчёта применить соотношение

d =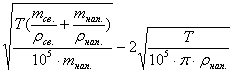

где mсв.и mнап.- масса связующего и наполнителя в образце, г, соответственно.

Указанное соотношение получено для модели равномерного распределения армирующих волоконец в поперечном сечении образца ПКМ. При этом суммарная площадь промежуточных слоёв определяется как разность общей площади поперечного сечения образца и суммарной площади поперечных сечений армирующих волоконец.

Решение

Ответ: d≈0,07 мм=0,007 см=70 мкм

7. Определить объём V, см3, децинормального (0,1 н) раствора соляной кислоты, пошедшего на нейтрализацию основных групп, содержащихся в 1 см3 смеси эпоксидная смола ЭД-20 -отвердитель полиэтиленполиамин (ПЭПА) по соотношению

V=N(1-xэп)vэп+(N-xэпN)vотв ,

где v =1,4∙10-20; vотв=3∙10-20 объём кислоты на нейтрализацию одной функциональной группы смолы и отвердителя, см3;

N=3,6∙1020 част/см3, N=1,8∙1020 част/см3 - начальные концентрации эпоксидных групп и аминогрупп отвердителя;

xэп=0,8 – степень превращения эпоксидных групп в процессе отверждения;

n≈2 – среднее количество эпоксидных групп, связываемых одной аминогруппой отвердителя.

Решение:

Расходующаяся при титровании хлористоводородная (соляная) кислота затрачивается главным образом на нейтрализацию эпоксидных групп смолы (первое слагаемое главного соотношения) и на нейтрализацию первичных аминогрупп отвердителя (второе слагаемое).Количество подлежащих нейтрализации кислотой основных групп определяется разностью начальных количеств и прореагировавших количеств указанных функциональных групп:

V=3,6∙10200,2∙1,4∙10-20(1,8∙1020- 0,4∙3,6∙1020)×

×3∙10-20=1,008+1,08=2,088

Ответ: V=2,088

8.Вычислить продолжительность ,с заполнения глухих пор наполнителя эпоксидным связующим вязкостью =7 Па∙с. Средняя длина пор =10 мкм, глубина заполнения =7 мкм, внешнее давление P1=8 МПа=8∙106 Па, начальное давление внутри поры P2=105 Па (атмосферное давление), радиус пор R=1 нм. Расчёт провести по соотношению

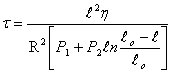
Что является движущей силой процесса заполнения пор, закрытых с одного конца (глухих пор)? Сформулируйте закон, который выражается используемым соотношением.

Решение:

Относительное заполнение поры 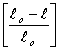< 1,поэтому n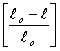< 0 есть

величина отрицательная, поэтому 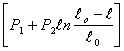есть разность давлений внешнего и внутри поры, то есть движущая сила процесса заполнения поры. Таким образом, продолжительность заполнения поры пропорциональна вязкости жидкого полимера и обратно пропорциональна движущей силе процесса. Для заполнения поры на 7 мкм (70% полной глубины) потребуется

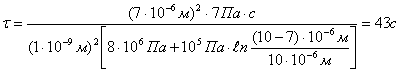
Ответ: τ=43 с

9.Вычислить толщину переходного слоя δ в системе, содержащей mсв=13 г фенольного связующего при содержании наполнителя (лавсан) 60% масс., если массовая доля переходного слоя γ=0,34.Удельная поверхность наполнителя Sуд=6 м2/г, плотность связующего ρ=1,2 г/см3. Расчёт вести по соотношению

δ= ,

где m- масса связующего на 1 г наполнителя.

Что такое переходный слой и где он локализуется?

Решение:

Среднюю толщину переходного слоя δ определяют как отношение объёма V переходного слоя к его поверхности, принимаемой равной поверхности наполнителя S=Sуд∙mнап (1).

Масса наполнителя mнап=(2)

Величина V=(3). С учетом соотношений (1-3) получаем:

δ=

Ответ: δ=0,03∙10-4 см=0,03 мкм

10. Методом обращенной газовой хроматографии (ОГХ) получено, что время удерживания τ паров этанола вискозной стренговой нитью (ВСН), помещенной в колонну хроматографа, составляет τ=50,5 с. Объемная скорость газа-носителя Vг=0,3 мл/с. Объем V сорбированного нитью пара этанола вычислить по соотношению V=Vг∙(τ-τо)=Vг∙Δτ (1), где τо=15 с – время удерживания несорбируемого компонента (“мёртвое” время колонки).

Считая пары этанола идеальным газом, следует найти количество молей и количество частиц в объёме V. При расчете суммарной поверхности S волокон принять, что сорбированный этанол покрыл поверхность мономолекулярным слоем, а площадь, занимаемая одной молекулой этанола, составляет δ=20∙10-20 м2. Найти удельную поверхность ВСН Sуд= (2) при массе нити m=4,618 г.

Что называют молем? Что такое удельная поверхность твердого материала?

Назовите основные части и принцип работы газового хроматографа.

Решение:

Количество молей n сорбированных паров находим с использованием объема одного моля идеального газа 22400 мл/моль: n=

Количество сорбированных молекул N определяем через число Авогадро А=6,02∙1023 частиц/моль:

N=n∙A

Поверхность сорбции S определяем как площадь мономолекулярного слоя:

S=δN=δnA.

Отсюда удельная поверхность Sуд:

Sуд=====≈12,13 м2/г

Ответ: S=56 м2; Sуд≈12 м2/г

11. Рассматривается процесс отверждения эпоксидной смолы ЭД-20.

Температурная зависимость изобарной мольной теплоёмкости этой смолы Сролиг, Дж/моль∙К, определяется соотношением

Сролиг=595+0,47Т+0,0002Т2 (1),

а температурная зависимость изобарной мольной теплоёмкости продукта с молекулярной массой 800 (димера) имеет вид

Српрод=7019-37,9Т+0,0607Т2 (2), то же для продукта с молекулярной массой 2000: Српрод 2000=17290-93,4Т+0,15Т2 (3).

Вычислить тепловой эффект отверждения при 100°С, если при 30°С он составляет -122 кДж/моль, по соотношению:

Q373=Q303+Δαo(373-303)+Δα1(3732-3032)+Δα2(3733-3033) (4)

Решение:

В данной задаче рассматриваются две модельные реакции

2 Ол.Прод 800 (I)

5 Ол.Прод2000 (II),

где Ол.- исходный олигомер со средней молекулярной массой 400.

В соответствии с правилами термодинамики величины Δαi рассчитываются по соотношениям:

Δαi=αi прод 800- 2αiдля реакции (I) и

Δαi=αi прод 2000- 2αiдля реакции (II)

1.Расчёт теплового эффекта реакции (I) при 373К:

Δαo=7019-2∙595=5829

Δα1=-37,9-2∙0,466=-38,832

Δα2=0,061- 0,00042=0,0605,

При этом обязателен учет знака коэффициентов αi:

Q373=-122000+5829∙70-19,416∙47320+0,02∙24076990=- 122000Дж/моль-29195 Дж/2 моль = -122000 Дж/моль –14597 Дж/моль ≈-137 кДж/моль

2.Расчёт теплового эффекта реакции (II) при 373 К:

∆αo=17290-5∙595=17290-2975=14315

∆α1=-93,36-5∙0,466=-93,36-2,33=-95,69

∆α2=0,15- 0,00021∙5=0,15-0,00105=0,14895

Q373=-122000+(14317∙70-0,5∙95,69∙47320+0,33∙0,14895∙24076990)=-122000+(1002190-2264025+1177112)=-122000+(2179302-2264025)=-122000-

-84723Дж/5моль=-122000 Дж-16945Дж ≈139 кДж/моль

Ответ: Q373=-122-15=-137 кДж/моль

Q373=-122-17=-139 кДж/моль

13. Найти поверхность S наполнителя в образце массой m=21,6 г при соотношении связующего и наполнителя 3:2 по массе, если в качестве наполнителя использована капроновая нить с удельной поверхностью Sуд=10 м2/г

Решение:

Материал содержит две массовые части из пяти, то есть 40% масс.

Следовательно , масса наполнителя mнап=21,6∙0,4=8,64 г.Суммарная поверхность S всех макрочастиц наполнителя

S=mнап∙Sуд=8,642∙10=86,4 м2

Ответ: S=86,4 м2

14. Найти во сколько раз кажущаяся поверхность Sрасч капроновой нити толщиной Т=2 текс, состоящей из 50 элементарных волокон, отличается от удельной поверхности Sуд=10 м2/г, плотность капрона ρ=1,14 г/см3. Элементарные волокна считать круглыми цилиндрами с поперечным сечением F= мкм2.Почему удельная (истинная) поверхность значительно больше кажущейся (расчётной) поверхности?

Решение:

Общее сечение нити F===1754 мкм2

Сечение элементарного волокна Fвол==35 мкм2

Условный радиус элементарного волокна r =3,34 мкм=

=3,34∙10-6 м.

Из сущности определения толщины в тексах: 2 г – 1000 м

1 г – 500 м =

Поверхность круглого элементарного волокна определяется в основном как поверхность круглого цилиндра: S==6,28∙3,34∙10-6 м∙500 м =

=21∙500∙10-6 м2=10488∙10-6 м2=0,0104876 м2≈0,0105 м2

Sрасч=nS=0,0104 м2∙50=0,52 м2/г

Искомое отношение Sуд/Sрасч=≈19

Большое отличие Sуд от Sрасч обусловлено тем, что при вычислении Sрасч не учитывали дефекты поверхности.

Ответ: ≈19

15. Исходя из выражений для средней степени превращения связующего в композиции x=xсв(1-γ)+yγ (1) и степени превращения связующего в переходном слое y=xсв+χ (2), вывести соотношение для вычисления параметра влияния χ (xсв- степень превращения связующего в объёме, γ- массовая доля связующего,образовавшего переходный слой).

Решение:

Подставив соотношение (2) в соотношение (1), получаем:

X=xсв-γxсв+γxсв+χγ

Отсюда χ=

Ответ: χ=

17. Степень превращения связующего y в переходном слое больше степени превращения связующего в объёме xсв на 0,18: y-xсв=χ=0,18. Пользуясь соотношением χ=(x-xсв)/γ=∆x/γ, найти массовую долю γ связующего, образовавшего переходный слой, если из кинетических результатов получено ∆x=0,10 (x-средняя степень превращения связующего в материале).Каково в этом случае влияние наполнителя на кинетику отверждения?

Решение:

Из соотношения χ=(x-xсв)/γ получаем : γ==0,55.

Из соотношений y>xсв, χ=y-xсв>0 видно, что степень превращения в переходном слое выше, чем в объёме, то есть наполнитель ускоряет отверждение.

Ответ: γ=0,55. Наполнитель ускоряет отверждение.

16. Найти скорость диффузии U=Δx/τ олигомерных молекул фенолоформальдегидной смолы к поверхности наполнителя по кинетическим данным:

τ,мин	x,масс. доли	xсв,масс. доли	Δx=x-xсв	(U,с-1)∙ ∙105	γ	χ=
30	0,33	0,30
60	0,67	0,60
90	0,90	0,80
120	0,92	0,84
150	0,94	0,88
180	0,95	0,91
210	0,96	0,94
240	0,97	0,96

Принято, что отверждение протекает в диффузионной области.Построить на миллиметровой бумаге график зависимости U(τ).Путем графического интегрирования графика U(τ) найти значения γ:

γτ=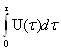 и вычислить значение параметра влияния χ.Заполните таблицу.

Решение:

Величина U= есть по существу скорость физико-химического взаимодействия между наполнителем и связующим.Для вычисления U продолжительность отверждения τ следует выразить в секундах. Величины Δx и U проходят через максимум, поэтому график U(τ) имеет экстремальную форму. Для графического интегрирования графика U(τ) необходимо:

1) определить количество массовых долей, приходящихся на 1 см2 площади графика – найти “цену” С одного квадратного сантиметра площади, ограниченной данным графиком;

2) выразить в квадратных сантиметрах площади Si полос, соответствующих продолжительности процесса 30;60;90;120;150;180;210;240 минут;

3) величина γ1=СS1; γ2=C(S1+S2); γ3=C(S1+S2+S3)…. γ8=C

Значения параметра влияния χ >1 не имеет реального смысла и обусловлены погрешностью данного метода расчёта.

Ответ: γmax=0,14; χmax=0,70

17. Определить среднюю толщину δ переходного слоя, образованного фенолоформальдегидным связующим массой m=12,96 г на поверхности S=86,4 м2 при массовой доле γ связующего, образовавшего переходный слой, γ=0,56. Плотность фенолоформальдегидного связующего ρ=1,2 г/см3.

Решение:

Средняя толщина переходного слоя определяется отношением объёма υ переходного слоя к его площади S:

δ=0,07∙10-4 см=0,07 мкм

Фенолформальдегидная смола образует на поверхности волокнистых наполнителей сравнительно тонкие переходные слои: 0,03 мкм – на поверхности лавсана (задача 9), 0,07 мкм – на поверхности капрона (задача 17).

Ответ: δ=0,07 мкм

18.Определить концентрации непрореагировавших олигомеров в объёме связующего С1 и в переходном слое С2, а также их разность ∆С=С2-С1 (движущую силу диффузии), если xсв=0,80; χ=0,17;γ=0,56.Общая масса связующего m=12,96 г. Расчет вести по модели 1 (см. рис.1):

Рис.1 Схема переходного слоя по модели 1

Подпись: Волокно

Переходный слой

Связующее в объёме

Плотность связующего ρ=1,2 г/см3.

В какую сторону диффундируют олигомерные молекулы в соответствии с полученными результатами ? Найти движущую силу диффузии ΔС=С2-С1.

Решение:

С1~ (1), С2~ (2), где V- объём связующего, υ- объём переходного слоя.

V= (3), υ= (4), y=xсв+χ (5).

Подставляя (3), (4), (5) в (1) и (2), получаем:

C1=масс. доли/см3=см-3

С2==0,00280 см-3

∆С=С2-С1=0,00280-0,04209=-0,03929≈-0,0393 см-3

Ответ: ∆С=-0,0393 см-3; олигомерные молекулы диффундируют из объёма связующего к поверхности наполнителя, т.к наполнитель ускоряет отверждение.

19. Определить среднюю толщину δ переходного слоя, образованного эпоксидным связующим массой m=12,96 г на поверхности наполнителя S=86,4 м2 при массовой доле связующего,образовавшего переходный слой,γ=0,90.Плотность эпоксидного связующего ρ=1,2 г/см3.

Решение:

Среднюю толщину переходного слоя можно оценить как отношение объёма переходного слоя υ к его поверхности S:

Δ=0,1125∙10-4 см=0,1125 мкм

Ответ: δ=0,1125∙10-4 см=0,1125 мкм

20. Вычислить коэффициент диффузии D, олигомерных молекул фенолоформальдегидного связующего к поверхности волокна капрон используя соотношение U=-DS(∆C/δ) (первый закон Фика), где скорость диффузии U=1,85∙10-5 с-1, движущая сила диффузии ∆С=-0,0393 см-3, толщина переходного слоя δ=0,07 мкм, площадь переходного слоя (поверхность диффузии) S=86,4 м2. S выразить в см2, δ- в см

Решение:

Из данного выражения первого закона Фика в конечных приращениях следует :

D1=-0,0382∙10-13=3,82∙10-15 см2/с.

Порядок полученной величины D1 соответствует известным значениям коэффициентов диффузии молекул низкомолекулярных веществ в твёрдых полимерах.

Ответ: D1=3,82∙10-15 см2/с

21. Вычислить коэффициент диффузии D2 олигомерных молекул фенолоформальдегидного связующего к поверхности волокна капрон, используя соотношение (второй закон Фика), где толщина переходного слоя (путь диффузии) δ=0,07 мкм, продолжительность процесса Δτ=90 мин. (необходимо Δτ выразить в секундах).

Решение:

Величины движущей силы диффузии ΔС=С2-С1 в левой и правой частях выражения для второго закона Фика в конечных приращениях сокращаются, поэтому указанное выражение принимает вид ,

откуда D2=.

Порядок величины D2 совпадает с порядком коэффициента диффузии D1, полученного в задаче 20 с использованием первого закона Фика. В принципе коэффициент диффузии D в обоих законах Фика – одна и та же величина.

Ответ: D2=8,98∙10-15 см2/с

22. Вычислить коэффициент диффузии D1 олигомерных молекул фенолоформальдегидного связующего к поверхности волокна капрон, используя соотношение U=-D1S(ΔC/δ) (первый закон Фика),где скорость диффузии U=1,85∙10-5 с-1, движущая сила диффузии ΔС=0,0377 см-3, толщина переходного слоя δ=0,07 мкм, площадь переходного слоя (поверхность диффузии) S=86,4 м2. S выразить в см2, δ- в см.

В данной задаче величина ΔС определена на основе модели 2 переходного слоя (рис.2)

Подпись: Волокно

Переходный слой

Связующее в объёме

Рис.2 Схема переходного слоя по модели 2

Решение:

D1=3,98∙10-15

Ответ: D1=3,98∙10-15 см2/с

23. Вычислить коэффициент диффузии D2 олигомерных молекул фенолоформальдегидного связующего к поверхности волокна капрон,используя соотношение (второй закон Фика), где ΔС – движущая сила диффузии, δ=0,07 мкм – толщина переходного слоя (путь диффузии), Δτ=90 мин. – продолжительность диффузии.

Следует δ выразить в см, τ- в секундах.

Решение:

Из данного выражения второго закона Фика в конечных приращениях получаем:

D2=

Из сравнения задач 21 и 23 следует, что при нахождении коэффициента диффузии с использованием второго закона Фика получаемое значение D не зависит от того, по какой модели переходного слоя рассчитывают величину ΔС, т.е величина ΔС в этом случае не имеет большого значения.

Ответ:D2=8,97∙10-15 см2/с

24. Используя приведённые кинетические данные зависимости степени превращения xсв ненаполненного эпоксидного связующего и степени превращения такого же связующего в смеси с волокнистым наполнителем (нить лавсан) от продолжительности отверждения τ, найти скорость U= взаимодействия между наполнителем и связующим. Графическим интегрированием зависимости U(τ) найти массовые доли γ связующего,образовавшего переходные слои γ=:

τ,мин	x,масс. доли	xсв,масс. доли	Δx=x-xсв	(U,с-1)∙ ∙105	γ	χ=
30	0,51	0,30
60	0,72	0,47
90	0,80	0,64
120	0,86	0,70
150	0,90	0,75
180	0,93	0,80
210	0,94	0,84
240	0,94	0,86

Вычислить также параметр влияния χ и указать, чему равна скорость диффузии олигомерных молекул связующего к поверхности элементов наполнителя, если отверждение протекает в диффузионной области.

Решение:

Для вычисления и U продолжительность отверждения τ следует выразить в секундах. Величины Δx и U проходят через максимум, поэтому график U(τ) имеет экстремальную форму. Для графического интегрирования графика U(τ) необходимо:

2) выразить в квадратных сантиметрах площади Si полос, соответствующих шагу Δτ=30 мин. при изменении τ от 0 до 240 минут (рис.3);

3) величина γ1=CS1, γ2=С(S1+S2), γ3=C(S1+S2+S3), ….. γ8=С=

Значения параметра влияния χ>1 не изменяют реального смысла и обусловлены погрешностью данного метода расчёта.

Сравнение результатов задач 24 и 16 показывает, что эпоксидное связующее образует более толстые (массивные) переходные слои, чем феноло-формальдегидное связующее (значения γmax составляют 0,63 и 0,14 соответственно). При этом в переходных слоях эпоксидного связующего выше роль химического взаимодействия между связующим и наполнителем (χmax составляет 0,96 и 0,70 соответственно).

Скорость диффузии олигомерных молекул связующего равны скорости U взаимодействия между связующим и наполнителем, если отверждение протекает в диффузионной области.

Ответ: γmax=0,63 χmax=0,96

25. Определить концентрации (массовые доли/см3) непрореагировавших олигомеров в объёме связующего С1 и в переходном слое С2, если степень превращения в объёме xсв=0,64; χ=0,35; γ=0,34. Общая масса связующнго m=12,96 г. Расчёт вести по модели 1 (то есть всё связующее, находящееся вблизи поверхности наполнителя, считать относящимся к переходному слою). Плотность связующего ρ=1,2 г/см3.

Найти движущую силу ΔС диффузии олигомерных молекул связующего в системе связующее-наполнитель. В какую сторону диффундируют олигомерные молекулы в данной задаче?

Решение:

Концентрацию С1 олигомеров в объёме связующего V можно оценить как массовую долю олигомеров в единице объёма: С~.

Аналогично концентрация в олигомеров в переходном слое С2~,

где степень превращения связующего в переходном слое y=xсв+χ=0,99.

Принимая плотности связующего в объёме и в переходном слое равными, можно вычислить объёмы:

V==7,128 см3;

υ ==3,672 см3

Используя приведённые соотношения, получаем:

C1==0,05050 см-3

С2=0,000926 см-3;

ΔC=C2-C1=-0,004957 см-3

Самодиффузия протекает в направлении от большей концентрации к меньшей, то есть из объёма к поверхности наполнителя, ускоряющего отверждение.

Ответ: С1=0,005050 см-3, С2=0,000926 см-3, ΔС=С2-С1=-0,04957 см-3

26. Определить концентрации (массовые доли/см3) непрореагировавших олигомеров в объёме связующего С1 и в переходном слое С2,если степень превращения в объёме xсв=0,64; χ=0,35; γ=0,34. Общая масса связующего m=12,96 г.Расчёт вести по модели 2 (то есть к переходному слою относить только отвержденные участки, находящиеся вблизи поверхности элементов наполнителя), при этом объём переходного слоя υ=myγ/ρ несколько сократится по сравнению с расчётом по модели 1 (y=xcв+χ – cтепень превращения олигомеров в переходном слое). Плотность связующего ρ=1,2 г/см3.

Найти движущую силу ΔС диффузии олигомерных молекул связующего в системе связующее-наполнитель.В какую сторону диффундируют олигомерные молекулы в данной задаче?

Решение:

По аналогии с задачей 25 концентрацию С1 олигомеров в объёме связующего V можно оценить как массовую долю олигомеров в единице объёма: C1~, концентрацию С2 олигомеров в переходном слое объёмом υ : С2~, где степень превращения связующего в переходном слое y=xсв+χ=0,99.

Принимая плотности связующего в объёме и в переходном слое равными, можно вычислить объёмы, исключив из переходных слоев неотвержденные участки (в соответствии с моделью 2):

V==7,165 см3;

υ==3,635 см3

Используя вышеуказанные соотношения, получаем:

C1==0,0524 см-3

С2==0,000935 см-3

ΔС=0,000935-0,05024=-0,04931 см-3

Таким образом, различие между величинами ΔС, рассчитанными при использовании моделей 1 и 2, невелико (см. задачу 25), так как при y1 различие между моделями 1 и 2 сглаживается.

Ответ: С1=0,05024 см-3; С2=0,000935 см-3; ΔС=С2-С1=-0,04931 см-3.

27. Вычислить коэффициент диффузии D1 олигомерных молекул эпоксидного связующего к поверхности волокна лавсан в процессе отверждения, используя соотношение U=-D1S(ΔC/δ) (первый закон Фика), где U=3,00∙10-5 масс. доли/с- скорость диффузии олигомеров, численно равная скорости взаимодействия связующего и наполнителя в диффузионной области; ΔС=-0,04957 масс.доли/см3- движущая сила диффузии, рассчитанная по модели 1 переходного слоя; масса полимерного образца m=21,6 г.; содержание наполнителя Снап=40 масс.%, удельная поверхность волокнистого наполнителя Sуд=6 м2/г; толщина переходного слоя δ=2 мкм.

Решение:

Величину коэффициента диффузии D1 находим из данного выражения для первого закона Фика:

D1=-, где S- поверхность диффузии, которую принимаем равной поверхности наполнителя:

S=mCнапSуд=21,6 г ∙0,4∙6 м2/г=51,84∙104 см2.

Используя полученное значение S, имеем:

D1=≈2,33∙10-13 см2/с

Ответ: D1=2,33∙10-13 см2/с

28. Вычислить коэффициент диффузии D2 олигомерных молекул эпоксидного связующего к поверхности волокна – наполнителя лавсан в процессе отверждения, используя соотношение (второй закон Фика), где движущая сила диффузии ΔС=-0,04957 масс. доли/см3 рассчитана по модели 1 переходного слоя, толщина переходного слоя (путь диффузии) δ=2 мкм; продолжительность отверждения Δτ=90 мин. при атмосферном давлении.

Решение:

В соответствии с данным выражением второго закона Фика величина движущей силы ΔС не играет существенной роли при вычислении D2:

D2==7,40∙10-12 см2/с=74∙10-13 см2/с

Получено ,что D2 примерно в 30 раз больше, чем D1 (cм. Задачу 27):

=31,8

Ответ: D2=7,40∙10-12 см2/с

29. Вычислить коэффициент диффузии D1 олигомерных молекул эпоксидного связующего к поверхности волокна лавсан в процессе отверждения, используя соотношение U=-D1S(ΔC/δ) (первый закон Фика), где U=3,00∙10-5 масс. доли/с – скорость диффузии олигомеров, численно равная скорости взаимодействия связующего и наполнителя в диффузионной области;ΔС=-0,04931 масс.доли/см3 – движущая сила диффузии, рассчитанная по модели 2 переходного слоя; масса полимерного образца m=21,6 г; содержание наполнителя Снап=40% масс., удельная поверхность волокнистого наполнителя Sуд=6 м2/ч; толщина переходного слоя δ=2 мкм.

Решение:

Величину коэффициента диффузии D1 находим из данного в условии выражения для первого закона Фика:

D1=-, где S – поверхность диффузии, которую принимаем равной поверхности наполнителя: S=m∙Cнап∙Sуд=21,6 г∙0,4∙6=51,8∙104 м2 используя полученное значение S, имеем:

D1=≈2,35∙10-13 см2/с

При использовании ΔС, рассчитанной по модели 1 переходного слоя, имели незначительное отличие величины D1 (cм. Задачу 27):

D1=2,33∙10-13 см2/с.

Ответ: D1=2,35∙10-13 см2/с.

30. Вычислить коэффициент диффузии D2 олигомерных молекул эпоксидного связующего к поверхности волокна – наполнителя лавсан в процессе отверждения, используя соотношение (второй закон Фика), где движущая сила диффузии ΔС=-0,04931 масс.доли/см3 рассчитана по модели 2 переходного слоя, толщина переходного слоя (путь диффузии) δ=2 мкм; продолжительность отверждения при атмосферном давлении Δτ=90 мин.

Решение:

Из данного в условии задачи соотношения получаем: D2==7,34∙10-12 см2/с

Сравнение результатов расчетов коэффициентов диффузии в задачах 27-30 по моделям 1,2 переходных слоёв:

D11=2,33∙10-13 см2/с; D12=2,35∙10-13 см2/с

D21=7,40∙10-12 см2/с; D22=7,34∙10-12 см2/с

показывает,что использование различных моделей переходных слоёв обусловливает меньшее различие в величине коэффициентов диффузии, чем использование различных законов диффузии.

Решение: D2=7,34∙10-12 см2/с.

31. Определить среднюю толщину прослойки эпоксидного связующего между волокнами, зная путь диффундирующих молекул в момент времени τ1, когда разбавляющее и замедляющее влияние волокнистого наполнителя компенсировано физико-химическим взаимодействием между связующим и наполнителем:

Х 1 1- с наполнителем; 2 – без наполнителя;

(x- cтепень превращения олигомерной термореактивной смолы в сетчатый продукт)

При расчёте исходить из того, что 2=d, и использовать соотношение D=∙, где D=6,0∙10-12 см2/с – коэффициент диффузии олигомерных молекул смолы, =10-7 см/с – средняя линейная скорость диффундирующих олигомерных молекул в рассматриваемом направлении.

Решение:

Из данного в условии задачи соотношения D=∙=∙ cледует:

==36∙10-5 см=3,6∙10-4 см=3,6 мкм

Ответ: =3,6∙10-4 см=3,6 мкм

32. Вывести в общем виде выражение для движущей силы ΔС диффузии олигомерных молекул в системе связующее-наполнитель, используя модель 1 переходного слоя, через параметры y,γ,χ (y-cтепень превращения связующего в сетчатый продукт в переходном слое); γ-массовая доля связующего, образовавшего переходный слой; y=xсв+χ, где xсв- cтепень превращения связующего в объёме; χ-параметр влияния. При выводе исходить из того, что ΔС=С2-С1 – движущая сила диффузии определяется разностью концентраций олигомеров в переходном слое С2 и в объёме С1.Концентрации определяются как отношение массовых долей олигомеров в переходном слое и в объёме связующего к соответствующим объёмам υ и V (γ(1-y)-количество олигомеров в переходном слое по модели 1).

Решение:

ΔС=С2-С1=

Учитывая, что =V, получаем:

ΔС=

Используя соотношение y=xсв+χ, окончательно имеем:

ΔC=

Ответ: ΔС=-

33. Вывести в общем виде выражение для движущей силы ΔС диффузии олигомерных молекул в системе связующее с массой и плотностью ρ – наполнитель, используя модель 2 переходного слоя, через параметры y,γ,χ (y-степень превращения связующего в сетчатый продукт в переходном слое; γ- массовая доля связующего, образовавшего переходный слой; y=xсв+χ, где xсв- степень превращения связующего в объёме; χ-параметр влияния. При выводе исходить из того, что ΔС=С2-С1 – движущая сила диффузии определяется разностью концентраций олигомеров в переходном слое С2 и в объёме С1. Концентрация определяется как отношение массовых долей олигомеров в переходном слое и в объёме связующего к соответствующим объёмам υ и V (γ(1-yγ)- количество олигомеров в переходном слое по модели 2).Общий объём связующего V определяется его массой m и плотностью ρ: V=m/ρ.

Решение:

ΔС=С2-С1=

Учитывая соотношение υ/γ=V, y=xсв+χ, получаем:

ΔC=

Ответ: ΔС==

34. Используя аддитивность тепловых эффектов отверждения ненаполненного эпоксидного связующего Q и взаимодействие Qдоп эпоксидного связующего с лавсаном, из которых складывается тепловой эффект суммарного процесса Qсумм=γQдоп+(1-γ)Q, найти величину Qдоп, если Qсумм=104 кДж/моль, Q=122 кДж/моль; массовая доля связующего, образовавшего переходный слой, γ=0,63.

Решение:

Выразив аддитивность тепловых эффектов отверждения ненаполненного эпоксидного связующего Q и взаимодействии Qдоп эпоксидного связующего с лавсаном, из которых складывается тепловой эффект суммарного процесса Qсумм=γQдоп+(1-γ)Q, найти величину Qдоп, если Qсумм=104 кДж/моль, Q=122 кДж/моль; массовая доля связующего, образовавшего переходный слой , γ=0,63.

Выразив Qдоп из соотношения, приведённого в условии задачи, и подставив численные значения величин, получаем:

Qдоп=

Ответ: Qдоп=94 кДж/моль

35. На основании известных экспериментальных значений тепловых эффектов отверждения эпоксидной смолы без наполнителя

Q=-122 кДж/моль, отверждения эпоксидной смолы с полипропиленовой нитью Qсумм=-132 кДж/моль и эффективных энергий активации, кДж/моль, отверждения эпоксидной смолы без наполнителя Е=27, эпоксидной смолы с полипропиленовой нитью Есумм=100 найти значения параметров А и В соотношения Е=А+В|Q|, считая, что значения А и В одинаковы для отверждения ненаполненных и наполненных систем.

Решение:

Применив зависимость Е от |Q| для ненаполненной и наполненной эпоксидной смолы, получаем систему двух линейных уравнений с двумя неизвестными:

27=А+122В

100=А+132В,

Откуда имеем: А=27-122В; 100=27-122В+132В;

10В=73; В=7,3

А=27-122∙7,3=-863,6≈-864 кДж/моль

Ответ: А=-864 кДж/моль; В=7,3.

36. Из соотношения Qдоп=200χ+20(1-χ) найти значения параметра влияния χ на основании известных значений теплового эффекта Qдоп взаимодействия между связующим и наполнителем для систем: эпоксидная смола ЭД-20 и полипропиленовая нить (ППН), анилино-фенолоформальдегидная смола СФ-342А и ППН-180 и 50 кДж/моль соответственно.

Решение:

Из данного в условии задачи соотношения следует, что тепловой эффект взаимодействия между связующим и наполнителем аддитивно складывается из теплоты химического (первое слагаемое) и физического (второе слагаемое) взаимодействия. Из этого соотношения следует: 180χ=Qдоп-20; χ=.

Применив последнее соотношение к смолам ЭД-20 и СФ-342А, получаем соответственно: χ1==0,89; χ2==0,17

Из полученных значений χ1>χ2 следует, что при взаимодействии наполнителя ППН со смолой ЭД-20 преобладают химические процессы, а при взаимодействии ППН со смолой СФ-342А- физические.

Ответ: χ1=0,89; χ2=0,17

37. Используя аддитивность тепловых эффектов отверждения ненаполненного связующего Q и взаимодействия Qдоп связующего с полипропиленовым наполнителем (ППН)

Qсумм=γQдоп+(1-γ)Q, вычислить массовые доли γ переходных слоев в системах эпоксидная смола+ППН (Q=122; Qcумм=132; Qдоп=180 кДж/моль) и фенолоформальдегидная смола+ППН (Q=21; Qсумм=23; Qдоп=50 кДж/моль) и толщину переходных слоёв δ= в тех же системах

(m=32 г- масса смолы на 1 г. наполнителя, ρ=1,2 г/см3- плотность связующего, она практически одинакова для обеих рассматриваемых смол; Sуд=5 м2/г- удельная поверхность полипропиленовой нити, используемой в качестве наполнителя).

С каким связующим ППН образует более толстые и прочные переходные слои?

Решение:

Из данного в условии соотношения аддитивности тепловых эффектов выражаем величину γ:

γ =

Подставляя в это соотношение численные значения тепловых эффектов, получаем для двух связующих:

γ1 ==0,172

γ2==0,069

Затем вычисляем соответственно среднюю толщину переходных слоёв

δ1 ==0,92∙10-4 см=0,92 мкм

δ2 = =0,37∙10-4 см=0,37 мкм

При взаимодействии ППН с эпоксидной смолой выделяется больше теплоты, чем при взаимодействии ППН с фенолоформальдегидной смолой:

180>50 кДж/моль. Таким образом, эпоксидная смола образует более толстые 0,92>0,37 мкм и прочные переходные слои.

Ответ: γ1=0,172; δ1=0,92 мкм;

γ2=0,069; δ2=0,37 мкм.

38. Используя аддитивность тепловых эффектов отверждения Q ненаполненной анилино-фенолоформальдегидной смолы СФ-342А и взаимодействия Qдоп этой смолы с лавсаном, из которых складывается тепловой эффект суммарного процесса Qсумм=γQдоп+(1-γ)Q, найти величину Qдоп, если Qсумм=65 кДж/моль, Q=21 кДж/моль; массовая доля связующего, образовавшего переходный слой, γ=0,56

Решение:

Из балансового уравнения тепловых эффектов, данного в условии задачи, находим:

Qдоп=≈100 кДж/моль

Отверждение анилино-фенолоформальдегидной смолы при повышенных давлениях ускорится капроном, тепловой эффект взаимодействия капрона с этим связующим сравнительно велик, величина Qдоп=100 кДж/моль близка к прочности химических связей между связующим и наполнителем.

Ответ: Qдоп=100 кДж/моль

39. На основании известных экспериментальных значений эффективной энергии активации отверждения смеси анилино-фенолоформальдегидной смолы СФ-342А с капроном Есумм=101 кДж/моль и суммарного теплового эффекта отверждения указанной смеси Qсумм=-65 кДж/моль. Найти параметр А соотношения Е=А+В|Q|.Параметр В=7,3 считать одинаковым для смол СФ-342А и эпоксидной ЭД-20.

Решение:

Из соотношения зависимости Е от |Q| выражаем :

А=Е-В|Q|=101-7,3∙65=101=-374 кДж/моль.

Указанное соотношение является уравнением прямой, в котором В-тангенс угла наклона прямой, А-значение Е при |Q|=0, то есть точка пересечения прямой с осью Е.

Ответ: А= - 374 кДж/моль.

40. Используя соотношение между энергией активации Е и тепловым эффектом Q; Е= - 864+7,3|Q| для отверждения эпоксидной смолы ЭД-20, вычислить абсолютные значения |Qдоп|, кДж/моль тепловых эффектов взаимодействия ЭД-20 с лавсаном и ППН, если энергии активации Едоп этих процессов составляют 43 и 172 кДж/моль соответственно.

Решение:

Выразим величину |Q| из данного соотношения: |Q|=.

Применяя это соотношение к процессу взаимодействия между связующим и различными наполнителями, получаем для лавсана:

|Qдоп|==124 кДж/моль

и для полипропиленовой нити:

|Qдоп|==142 кДж/моль

Полученные значения |Qдоп| и |Qдоп| свидетельствуют о том, что эпоксидная смола образует с полипропиленом более прочные химические связи, чем с лавсаном.

Ответ: |Qдоп|=124 кДж/моль

|Qдоп|=142 кДж/моль

41. Используя соотношение Е=-374+7,3|Q| между энергией активации Е и тепловым эффектом Q для отверждения анилино-фенолоформальдегидной смолы СФ-342А, вычислить абсолютные значения |Qдоп|,кДж/моль, тепловых эффектов взаимодействия смолы СФ-342А с ППН при повышенном (8 МПа) и атмосферном давлении, если энергии активации этих процессов Едоп составляют 34 и 21 кДж/моль соответственно.

Решение:

Выразим величину |Q| из данного в условии соотношения: |Q|=.

Применив это соотношение к процессу взаимодействия между связующим и наполнителем, получаем величины |Qдоп| при повышенном и |Qдоп| при атмосферном давлении соответственно:

|Qдоп|==56 кДж/моль,

|Qдоп|==54 кДж/моль.

Полученные значения показывают, что величина давления практически не влияет на прочность физико-химических связей, образующихся между смолой СФ-342А и полипропиленовой нитью.

Ответ: |Qдоп|=56 кДж/моль; |Qдоп|=54 кДж/моль.

42. Используя соотношение γ=А (1), аналогичное соотношению Вант-Гоффа для константы равновесия K: K=A(2), где А-предэкспоненциальный множитель; Qдоп- тепловой эффект взаимодействия между связующим и наполнителем; Q- тепловой эффект рассматриваемого обратимого процесса, найти массовую долю γ2 переходного слоя в системе анилино-фенолоформальдегидная смола СФ-342А – полипропиленовая нить ППН при температуре Т2=443 К, если при Т1=393 К известно значение γ1=0,38. Тепловой эффект Qдоп взаимодействия ППН со связующим в данном случае составляет Qдоп=-45 кДж/моль. Рекомендуется записать соотношение (1) в логарифмической форме для температуры Т1 и для температуры Т2.

Решение:

Записываем соотношение (1) для температур Т1 и Т2:

γ1 =A (2)

γ2=A(3)

Почленно логарифмируем соотношения (2) и (3):

(4)

(5),

из соотношения (4) вычитаем соотношение (5):

откуда . Подставив сюда значения всех величин из условия задачи, получаем:

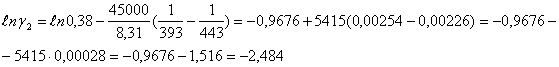
10-1,08=10-2∙100,92=8,3∙10-2=0,083.

Результат показал, что при повышении температуры отверждения массовая доля переходного слоя уменьшается, так как взаимодействие между наполнителем и связующим – экзотермический процесс.

Ответ: .

43. Равновесная деформация жгута из диацетатных нитей при усилии Р=0,7 Н составила Δ=2,34 мм (однонаправленное растяжение). Начальная длина жгута между зажимами =140,0 мм, текс жгута t=554 (то есть

1000 м такого жгута имеют массу 554г.).Испытания проводились при Т=413 К. Плотность диацетата целлюлозы ρ=1320 кг/м3.

Вычислить относительную деформацию ε , площадь поперечного сечения S, мкм2 по соотношению S=1000t/ρ (1), где ρ выражено в г/см3.

Далее определить напряжение в жгуте σ= (2), модуль упругости

ЕР= (3) и среднюю массу молекулярных цепей между узлами сетки

MC= (4), где ρ- плотность, кг/м3; R- универсальная газовая постоянная R=8,31 Дж/моль∙К. В каких единицах выражается напряжение σ и модуль упругости Е в системе СИ?