Контрольная работа: Адсорбция полиэлектролитов

Содержание

1. Теоретические модели адсорбции полиэлектролитов

1.1 Приближения среднего поля

1.2 Профили распределения

1.3 Влияние полиэлектролитов на отталкивание двойных электрических слоев

1.4 Мостиковое притяжение, обусловленное полиэлектролитами

1.5 Несимметричные системы

1.7 Энергетические мостики

2. Необратимость адсорбции полимеров

3. Измерение адсорбции полимеров

1. Теоретические модели адсорбции полиэлектролитов

Коммерчески доступен широкий спектр разнообразных полиэлектролитов, различающихся структурой и топологией. Одним из простых примеров является полиэтиленимин - положительно заряженный полимер с группами - СН2-СН2-между атомами азота, протонированного при нормальных рН.

В промышленных образцах полиэтиленимин сильно разветвлен и линейными оказываются только димеры и тримеры. Аминокислоты, например глутаминовую кислоту или лизин, можно полимеризовать для получения анионных и катионных полиэлектролитов соответственно. Заряд в этих случаях локализуется в боковых цепях полимера. В первом простом приближении можно предположить, что эти детали не так важны и что главный эффект заключается в том, что в полиэлектролите имеются связанные заряды. Учитывая это предположение, полиэлектролит можно представить моделью "ожерелья" из зарядов, связанных между собой жесткими связями или гармоническими пружинами. Все теории, обсуждаемые ниже, построены на этом предположении.

1.1 Приближения среднего поля

Все известные из литературы теории для полиэлектролитов, адсорбированных на твердых поверхностях, основаны на различных приближениях среднего поля.

Некоторые теории включают решеточное приближение, например теория Брэгга-Вильямса, другие рассматривают непрерывные цепи. Ниже кратко обсуждаются несколько подходов, использующихся для описания адсорбции полиэлектролитов и влияния адсорбции на силы взаимодействия между частицами.

Такие исследования активно развиваются и приведенные ниже сведения не являются исчерпывающими.

Рис.1. Схематическое представление простой модели полиэлектролита, состоящего из заряженных мономерных единиц, связанных между собой упругими пружинами. Пружины моделируют не индивидуальные химические связи, а отражают число связей между заряженными атомами

Теория Схойтенса-Флира {Scheutjens-Fleer). Это наиболее общая теория, разработанная для описания адсорбции полимеров и полиэлектролитов; она оказалась очень хорошей моделью адсорбции полимеров. Теория дает хорошее согласие с экспериментом, но в ней используется много параметров. По выражению авторов: "все результаты и закономерности объяснимы в рамках нашей теории при использовании разумных значений параметров". Одно из преимуществ теории заключается в том, что она применима к полимерам с достаточно длинными цепями. В то же время теория Схойтенса-Флира редко используется для расчета взаимодействий.

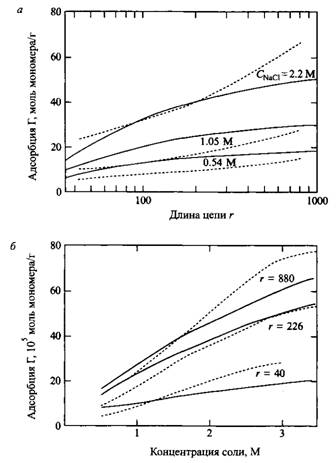
Рис.2. Зависимость адсорбции полиэлектролита от длины цепи г и ионной силы Cs. Сплошные линии представляют оценки по теории Схойтенса-Флира, штриховые линии - экспериментальные результаты

Теория Миклавица-Марцелья {Miklavic-Marcelja). Эта теория рассматривает на поверхности только одиночную цепь и полностью пренебрегает влиянием других адсорбированных цепей. Рассмотрение ограничено короткими цепями. Преимущество этой теории состоит в том, что она позволяет определить исключенный объем в пределах цепи.

Теория адсорбции полиэлектролитов Пуассона-Больцмана. Это прямое распространение уравнения Пуассона-Больцмана на непрерывную цепь. Этот подход, не являясь теорией адсорбции, оказался эффективным для предсказания сил взаимодействия, что было установлено сравнением с результатами, полученными при моделировании методом Монте-Карло. Теория ограничена короткими цепями, результирующее уравнение может быть решено только численно. Теория Подгорника и Офейсдена {Podgornik, Opheusden). Теория рассматривает бесконечно большую непрерывную цепь между двумя заряженными стенками. Справедливость такой модели еще предстоит доказать, в то же время качественно она удовлетворительно описывает некоторые важные физические свойства.

1.2 Профили распределения

Распределение и конфигурация полиэлектролитов с внешней стороны заряженной поверхности, в принципе, можно определить путем исследования рассеяния света, несмотря на сложность интерпретации результатов. Косвенную информацию можно получить из измерений гидродинамического радиуса. Из рис. 16 и 18 видно, что полиэлектролиты адсорбируются на противоположно заряженных поверхностях в плоской конформации, в то время как при адсорбции на одноименно заряженных или нейтральных поверхностях они принимают более вытянутые формы. В первом случае результат можно объяснить электростатическим притяжением между поверхностью и полимерной цепью во втором - отталкиванием между цепями. Введение соли слабо влияет на профиль распределения.

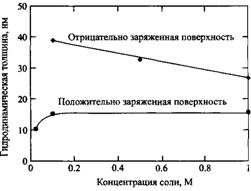
Рис.3. Зависимость гидродинамической толщины адсорбционного слоя полистиролсульфоната на частицах полистирольного латекса от ионной силы раствора

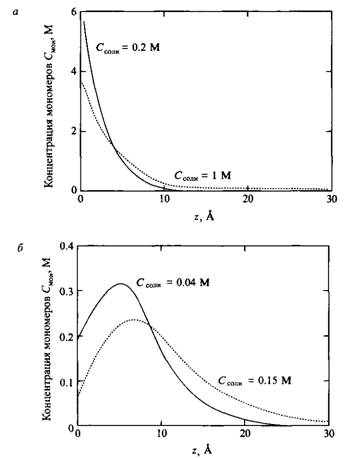
Рис.4. Профили распределения заряженных мономеров полиэлектролитов, адсорбировании концевыми группами на поверхности двух противоположно заряженных стенок, расположенных н расстоянии 60 А. Показана только половина системы, одна из стенок находится при ж = 0. а - Высокая поверхностная плотность заряда; б - низкая плотность поверхностного заряда. Моделировани методом Монте-Карло

1.3 Влияние полиэлектролитов на отталкивание двойных электрических слоев

Добавление гибких полиэлектролитов к заряженным коллоидам оказывает сильное влияние на взаимодействие в системах и может приводить к стабилизации и к дестабилизации дисперсий. Эти эффекты широко используются в раз личных технологиях, например в производстве бумаги, в пищевой промышленности, а также при очистке воды. Биологические системы тоже содержат гибкие полиэлектролиты, например спермин и спермидин, способствующие упаковке ДНК в нативную конформацию и участвующие в процессе коагуляции крови, а также гликолипиды на поверхности мембран.

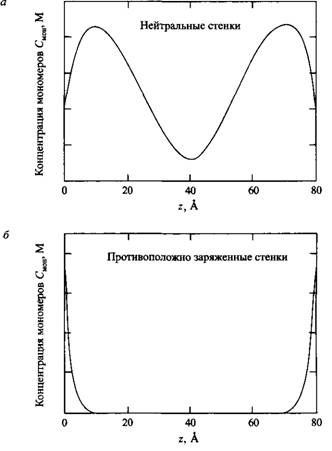
Рис.18. Профили распределения заряженных мономеров при адсорбции полиэлектролита концевыми группами на поверхности двух стенок: стенки не заряжены, стенки несут заряд, противоположный по знаку заряду полиэлектролита

Взаимодействия в присутствии полиэлектролитов разнообразны, и нельзя ожидать, что на основании уравнения Пуассона-Больцмана можно объяснить все наблюдаемые эффекты. На самом деле во многих случаях системы не подчиняются теории ДЛФО. Рассмотрим несколько идеализированных ситуаций на основе упрощенных моделей полимера, учитывающих два важных свойства - связность и гибкость. Они особенно важны, когда полиэлектролиты взаимодействуют с заряженными поверхностями и модулируют взаимодействия между ними.

1.4 Мостиковое притяжение, обусловленное полиэлектролитами

Рассмотрим простую систему, состоящую из двух заряженных поверхностей, структура ДЭС которых обеспечивает сильное отталкивание между ними. Теперь превратим ионы в полиэлектролитные цепи, связав их пружинками, как показано на рис. Таким образом, вместо противоионов получим гибкие полипротивоионы. Для них возможны три ситуации:

1) Связана только часть противоионов, образуется "недокомпенсированная" система.

2) Все противоионы связаны, образуется идеально скомпенсированная система.

3) При добавлении соли часть ее ионов также связывается, формируется "перекомпенсированная" система.

В идеально скомпенсированной системе исходное отталкивание двух ДЭС полностью исчезает и появляется очень сильное притяжение на близких расстояниях. Дополнительное притяжение возникает в результате образования мостиков из полиэлектролитных цепей на малых расстояниях. Движущая сила образования мостиков имеет энтропийную природу. На больших расстояниях между поверхностями цепи удерживаются "своими" поверхностями. В этом случае энтропия цепей мала. Уменьшим расстояние между поверхностями. Когда оно станет сопоставимым с расстоянием мономер-мономер, цепи могут за счет небольшой потери электростатической энергии образовать мостики между поверхностями и таким образом сильно увеличить энтропию.

Осмотическое давление можно определить с помощью так называемой контактной теоремы.

Для полиэлектролита контактное соотношение должно быть модифицировано с учетом члена, учитывающего образование мостиков:

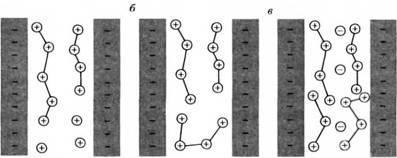
Рис.5. Две плоские заряженные стенки, нейтрализованные полиэлектролитами и простыми небольшими ионами: а - "недокомпенсированная" система, в которой только часть противоинов связана; б - идеально скомпенсированная система, в которой все противоины связаны; в - "перекомпенсированная"система, содержащая дополнительное количество связанных ионов соли

Рис.6. Зависимость осмотического давления Р0см от расстояния в идеально скомпенсированной системе с гибкими полипротивоионами и в двойном электрическом слое с не связанными с поверхностью небольшими ионами

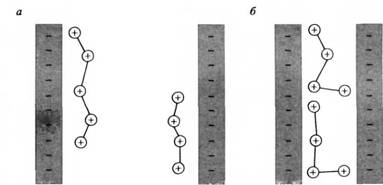
Рис.7. Схематическое представление механизма мостикообразования: а - мостики не образуются и Pocm = 0; б - интенсивное образование мостиков и Pocm < 0

Третий член в уравнении приобретает особо важное значение в системах с двухзарядными противоионами. На рис. дано сравнение вкладов энтропийного члена ATc и мостикового члена рМОст в зависимости от расстояния между поверхностями. Положение, отвечающее минимуму взаимодействия, находится на расстоянии, приблизительно равном расстоянию между двумя мономерами в полиэлектролите, и изменяется приблизительно как обратная величина квадратного корня из расстояния между мономерами.

До сих пор обсуждались теоретические результаты, и теперь справедливо задать вопрос, подтверждены ли эти результаты прямыми экспериментами. Рисунок представляет результаты измерения поверхностных сил между двумя поверхностями слюды, причем в одном эксперименте силы измерялись в растворе KBr с концентрацией 10-4 М, а в другом - после добавления полиэлектролита.

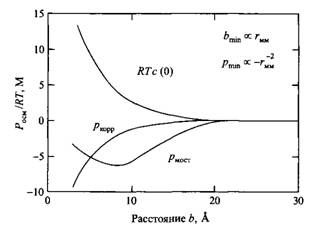
Рис.22. Зависимости различных компонент осмотического давления в идеально скомпенсированном двойном электрическом слое полиэлектролита от расстояния

Рис.8. Зависимость сил взаимодействия между двумя поверхностями слюды от расстояния между ними в растворе KBr и в 10М растворе KBr с добавкой полиэлектролита. Данные экспериментального измерения поверхностных сил

В качестве полиэлектролита использовали хлорид полипропил) триметиламмония, имеющий следующую химическую структуру:

Введение МАРТАС полностью устраняет отталкивание ДЭС, притяжение регистрируется на расстоянии - 100 А. Увеличение концентрации соли до 10 M снова приводит к появлению отталкивания ДЭС. Такой результат можно объяснить увеличением адсорбции при увеличении концентрации соли.

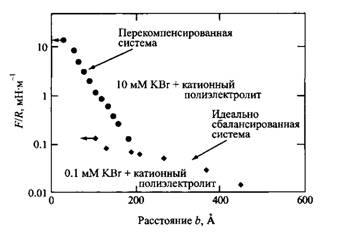
Рис.9. Зависимость сил взаимодействия между двумя поверхностями слюды от расстояния между ними в растворе МАРТАС, содержащем 104 M KBr и 10-2M KBr

Соль экранирует заряды полиэлектролита, уменьшая отталкивание между ними, и заряженные стенки адсорбируют дополнительное число цепей, большее, чем это необходимо для нейтрализации. В результате происходит перезарядка, что соответствует "перекомпенсированной" системе. Кроме того, отталкивание может появиться, если количество адсорбированного полимера меньше, чем это требуется для нейтрализации поверхности. В обоих случаях регистрируемся обычное отталкивание двойных электрических слоев, и только в почти идеально "скомпенсированной" системе отталкивание ДЭС исчезает.

В обычных системах, подчиняющихся теории ДЛФО и содержащих ионы малых размеров, дополнительное введение электролита почти всегда приводит к уменьшению отталкивания. В системах, содержащих полиэлектролит, возможно противоположное явление, поскольку концентрация соли напрямую влияет на количество адсорбированного полиэлектролита и на конформацию его молекул на поверхности. Добавление соли приводит и к более тонким эффектам, поскольку влияет на равновесие Доннана. Солевой баланс в системах с обычными двойными электрическими слоями и в системах, содержащих полиэлектролит, качественно различается, что отражает рис.

1.5 Несимметричные системы

Дополнительное притяжение наблюдалось экспериментально и рассчитано теоретически для несимметричных систем, в которых на одной стенке адсорбирован полиэлектролит, а другая стенка представлена свободной заряженной поверхностью. Чтобы установить источник притяжения, необходимо еще раз обратиться к контактной теореме. Выше предполагалось, что обе половины системы в среднем электронейтральны. Если это условие не соблюдается, необходимо ввести дополнительное слагаемое:

где уп - плотность заряда на каждой стенке. Притяжение на очень больших расстояниях может быть следствием асимметрии заряда. Движущей силой возникновения асимметрии заряда обычно является энтропия смешения противоионов. Будет ли сила асимптотически силой притяжения или отталкивания зависит от концентрации соли и от свойств заряженных поверхностей.

Нейтральные стенки.

Обычные ДЭС, на которые мы неоднократно ссылались, создаются поверхностными заряженными группами или адсорбированными ионами, как в золе AgI. Можно предположить, что заряд на ранее нейтральной поверхности возникает вследствие адсорбции на ней полиэлектролита. Фактически такая ситуация близка к "перекомпенсированной" системе, которая обсуждалась ранее. Полиэлектролиты, адсорбированные на нейтральной поверхности, конечно, нейтрализуются противоионами. Противоионы в силу энтропийных причин, будут распределяться в растворе и "тянуть" за собой цепи, что приведет к вытянутым конфигурациям цепей. Их "вытянутость" сильно зависит от концентрации соли. Это еще один пример важности энтропийного фактора и того обстоятельства, что свойства заряженного полимера определяются его противоионами. Взаимодействие на больших расстояниях между двумя такими полиэлектролитными "щетками" аналогично взаимодействиям обычных ДЭС, несмотря на то что расстояние в уравнении Пуассона-Больцмана не равно расстоянию между стенками и должно быть изменено с учетом вытянутости полимера. Приближенно можно использовать уравнение:

На малых расстояниях взаимное проникновение цепей приведет к появлению дополнительного отталкивания.

1.7 Энергетические мостики

Еще один тип мостиков реализуется между конечными заряженными агрегатами, например между мицеллами или частицами золей. Такая ситуация схематически представлена на рис.25. Полиэлектролитная цепь нейтрализует две частицы или более. Если агрегаты находятся далеко друг от друга, цепь захватывается одним из агрегатов, и взаимодействие проявится как слабое притяжение. На промежуточных расстояниях цепь может образовать мостик между обеими частицами, что очень выгодно с энергетической точки зрения и является причиной сильного притяжения движущая сила образования таких мостиков состоит в нейтрализации агрегатов.

Главная:

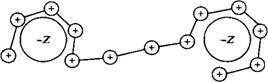
Рис.10. Схематическое представление взаимодействия полиэлектролитной цепи с двумя сферическими частицами, несущими противоположный по знаку заряд

Таким образом, можно говорить о мостиках "энергетического" типа в отличие от мостиков "энтропийного" типа.

Добавление полиэлектролитов к заряженным коллоидным системам индуцирует притяжение, но может вызывать и силы отталкивания. Большие концентрации солей экранируют электростатические взаимодействия между коллоидными частицами и полиэлектролитными цепями. В итоге это может приводить либо к увеличению отталкивания, либо к увеличению притяжения. Таким образом, электростатика может отвечать за множество эффектов, которые характерны для систем, содержащих полиэлектролит. Специфические взаимодействия полимер-поверхность, безусловно, еще больше усложняют картину.

2. Необратимость адсорбции полимеров

Вопрос об обратимости адсорбции полимеров исследовался во многих работах. Вывод можно сформулировать следующим образом: несмотря на то что адсорбция полимера может быть обратимой, практически полимер адсорбируется необратимо. Это кажущееся противоречие объясняется замедленной динамикой полимерных систем. Чтобы полимер десорбировался с поверхности, все его сегменты, закрепленные на поверхности, должны открепиться от нее почти одновременно. При отсоединении от поверхности только небольшой части сегментов высока вероятность адсорбции других сегментов, прежде чем произойдет десорбция всей молекулы полимера. Следовательно, полимерная цепь остается на поверхности за счет собственной "инерции". Это аналогично инерции, вызывающей "более медленное заполнение автобуса по сравнению с движением каждого отдельного человека". Можно считать, что в течение ограниченного периода времени полимеры адсорбируются необратимо, в то время как для очень больших времен адсорбция полимера все-таки обратима.

На этом свойстве основаны разнообразные применения полимеров для модифицирования поверхностей.

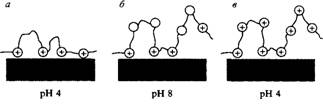
Рис.12. Схема адсорбции полиэтиленимина на отрицательно заряженной поверхности, показывающая, что в результате кажущейся необратимости адсорбции можно изменить заряд поверхности на положительный

В качестве примера на рис.26 показано, как с помощью полиэлектролита можно изменить заряд поверхности. Здесь для перезарядки поверхности, заряд которой создан анионами, используется катионный полимер полиэтиленимин. При рН 4 катионный полимер имеет максимальный заряд и сильно адсорбируется на анионной поверхности, приводя к идеально сбалансированной системе. Однако это конфигурация полимера в адсорбированном состоянии не сообщает поверхности положительного заряда. При адсорбции полимера из растворов с более высокими рН, когда только некоторая доля катионных мест заряжена, полимер адсорбируется в состоянии клубка. После адсорбции полимера рН системы доводят до 4 и ранее адсорбированный полимер полностью ионизуется, сообщая поверхности избыточный катионный заряд, т.е. давая "перекомпенсированную" систему. Указанный способ модифицирования поверхности основан на инерции полимера, так как полимеру не дается времени, чтобы десорбироваться и достичь равновесного состояния, отвечающего рН 4. Однако в течение достаточного длительного времени система отрелаксирует с переходом в конфигурацию, представленную на рис.26, я.

Концепция кислот и оснований Льюиса для описания адсорбции полимеров.

Концепция льюисовских кислот и оснований была успешно использована для описания адсорбции полимеров из растворов. Льюисовские кислоты - это акцепторы электронных пар, а льюисовские основания - доноры электронных пар. Соответствующие примеры - хлороформ и тетрагидрофуран. В процесс адсорбции конкурентно включены три компонента: полимер, растворитель и поверхность. Для описания адсорбции оказалось возможным использовать кислотно-основную концепцию. На рис.27 представлена адсорбция полиметилметакрилата на поверхности кремнезема. Адсорбцию проводили из растворов в различных растворителях, отличающихся по кислотности или основности. Растворители классифицировали по их кислотности или основности. Слева находятся сильноосновные растворители, адсорбция полимера в этих системах не наблюдается из-за конкуренции за поверхность между основным полимером и основным растворителем. Причем чем выше основность растворителя, тем меньше адсорбция ПММА. С правой стороны, где расположены кислотные растворители, картина обратная. Низкая адсорбция полимера наблюдается вследствие конкуренции за основный полимер между кислотной поверхностью и кислотным растворителем. Чем более кислотный растворитель, тем больше к нему сродство основного полимера, что приводит к уменьшению адсорбции на поверхности меньшей кислотности. В случае нейтрального растворителя достигается максимальное значение адсорбции. Эти свойства находят технологическое применение. На рис.28 приведены зависимости модуля упругости пластика ПММА от объемной доли кремнеземного наполнителя. Пластик получали из двух растворителей - тетрагидрофурана и из метиленхлорида. Видно, что модуль увеличивается с увеличением содержания наполнителя для ПММА, полученного из раствора в метиленхлориде, и почти не изменяется для ПММА, полученного из раствора в тетрагидрофуране. Плохие характеристики второй системы являются следствием адсорбции основного тетрагидрофурана на наполнителе, что затрудняет контакт полимера с поверхностью кремнезема, поэтому механическая прочность мала. Для получения высокомодульного пластикового литья необходимо использовать растворитель с низким сродством к поверхности наполнителя.

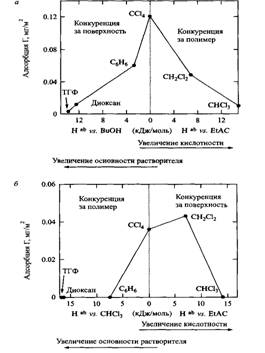
Рис.13. Адсорбция ПММА на кремнеземе и адсорбция хлорированного поливинилхлорида на карбонате кальция из различных растворителей, отличающихся кислотно-основными свойствами.

Аналогичное рассмотрение на основе представлений о льюсовских кислотах и основаниях, безусловно, применимо и для адсорбции кислотного полимера на поверхности основного твердого тела. На рис.27, б представлены данные по адсорбции хлорированного поливинилхлорида на карбонате кальция из растворителей, различающихся по кислотно-основным свойствам.

Конкуренцию между полимером и растворителем за поверхность можно определить достаточно точно, выполнив следующий эксперимент. Сначала изучают адсорбцию полимера на поверхности твердого тела из нейтрального растворителя. Затем добавляют другой растворитель, обладающий некоторым сродством к поверхности и вследствие этого конкурирующий с полимером за центры адсорбции. При высокой концентрации второго растворителя полимер полностью десорбируется с поверхности. Такой растворитель получил название "вытеснителя".

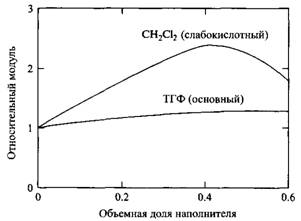
Рис.28. Зависимости относительного модуля упругости ПММА от объемной доли наполнителя для различных образцов пластика, приготовленных из метиленхлорида и тетрагидрофурана

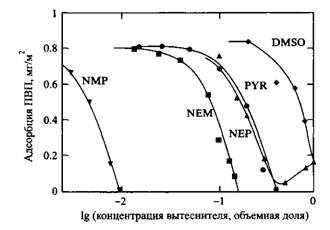
Рис.15. Зависимость десорбции поливинилпирролидона с поверхности кремнезема в водных растворах от концентрации вытеснителей. Видно, что полимер полностью десорбируется при критической концентрации каждого вытеснителя

Из рис.15 видно, как поливинилпирролидон непрерывно десорбируется с поверхности кремнезема в водной среде по мере повышения концентрации вытеснителя вплоть до достижения критической концентрации, при которой полимер полностью десорбируется с поверхности.

Наиболее эффективным вытеснителем оказался Н-метилпирролидон: он способен полностью десорбировать ПВП при объемной доле в воде - 1%, в то время как диметилсульфоксид даже в чистом виде полностью не вытесняет полимер с поверхности.

Эти результаты хорошо коррелируют с адсорбционной активностью вытеснителей по отношению к кремнезему в воде. Адсорбционная активность при низких концентрациях пропорциональна наклону изотермы адсорбции.

Различные вытеснители характеризуются следующими значениями адсорбционной активности: 4300 - NMP, 44 - Н-этилморфолин, 5.3 - пиридин, 3.5 - Н-этилпирролидон, 2.8 - ДМСО. Таким образом, чем сильнее адсорбируется вытеснитель, тем меньше его нужно добавить для полного удаления полимера с поверхности.

Можно сделать вывод, что для "отмывания" полимера с поверхности необходимо использовать вытеснитель, у которого сродство к поверхности выше, чем у полимера.

3. Измерение адсорбции полимеров

Чаще всего адсорбцию полимера измеряют по убыли концентрации в растворе после адсорбции на поверхности дисперсных частиц. К определенному объему раствора полимера известной концентрации добавляют частицы, например латекса или пигмента. После достижения равновесия частицы отделяют и определяют равновесную концентрацию полимера в растворе. Довольно часто возникают проблемы с выбором подходящего и точного метода определения концентрации полимера. В том случае, если нужно получить оценочные результаты, можно воспользоваться альтернативным методом определения электрофоретической подвижности частиц при электрофорезе в электрическом поле. Электрофоретическая подвижность является мерой потенциала на границе скольжения вблизи поверхности частицы. Потенциал зависит от расстояния от поверхности частицы. При адсорбции на поверхности частицы неионного полимера граница скольжения смещается от поверхности частицы вглубь раствора, поэтому определяемое значение абсолютной электрофоретической подвижности, или дзета-потенциала, будет пониженным.

Такие измерения выполняются быстро и служат характеристикой взаимодействия полимера с поверхностью частицы. Адсорбцию ионных полимеров на поверхности частиц также можно определять по электрофоретической подвижности при соблюдении некоторой осторожности, поскольку результаты не всегда оказываются однозначными.

Адсорбцию полимера на макроскопических поверхностях удобно измерять методом эллипсометрии. Эллиптически поляризованный свет отражается поверхностью, на которой адсорбирован полимер. Поляризация отраженного света чувствительна к полимерному слою. Этот метод позволяет одновременно определять величину адсорбции и толщину адсорбционного слоя.

Адсорбцию полимера на границе вода-воздух легко определить по поверхностному натяжению. Полимер может сильно влиять на поверхностное натяжение даже при низких концентрациях. Резкое понижение поверхностного натяжения связано с низкой растворимостью полимера.

На основании измерений поверхностного натяжения легко показать макромолекулярную природу адсорбции полимера. Рассмотрим адсорбцию полиметакриловой кислоты из водного раствора на поверхности раствор-воздух. В качестве модели мономерного звена выберем изомасляную кислоту. Прежде всего постулируем, что поверхностной активностью обладают неионизованные молекулы, которые и адсорбируются на поверхности жидкость-воздух. При степени ионизации, равной нулю, поверхностное натяжение, характеризующее адсорбцию, имеет самое низкое из возможных значений как для полимера, так и для мономерной системы. Как следствие, поверхностное натяжение будет максимальным при очень высокой степени ионизации.

Из рис.16, а видно, что поверхностное натяжение растворов изомасляной кислоты линейно увеличивается со степенью ионизации. Для раствора полимера наблюдается скачок поверхностного натяжения при степени ионизации - 0.1. Причина скачка заключается в полимерной природе поверхностно-активного компонента. При повышении степени ионизации отдельные сегменты адсорбированного полимера ионизуются, но при этом остается еще довольно много неионизованных сегментов, удерживающих полимер в адсорбированном состоянии. При критической степени ионизации полимер полностью десорбируется с поверхности, вызывая скачок поверхностного натяжения. Для наглядности здесь можно провести аналогию с пробками, плавающими на поверхности. Процесс диссоциации моделируется подвешиванием к пробке гирек, втягивающих ее внутрь жидкости. В том случае, если пробки связаны веревкой, они все останутся на поверхности вплоть до достижения критической массы, после чего поверхность сразу освобождается от пробок.

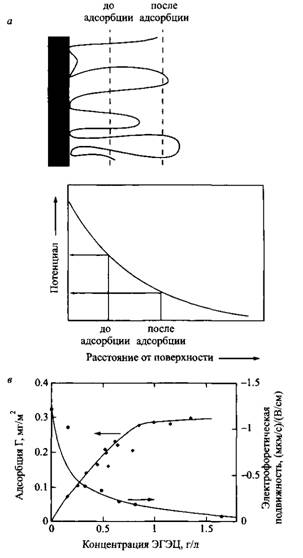
Рис.16. Изменение электрофоретической подвижности частиц при адсорбции незаряженного полимера. Адсорбированный полимер целлюлоза) сдвигает плоскость скольжения от поверхности вглубь раствора, приводя к уменьшению электрофоретической подвижности

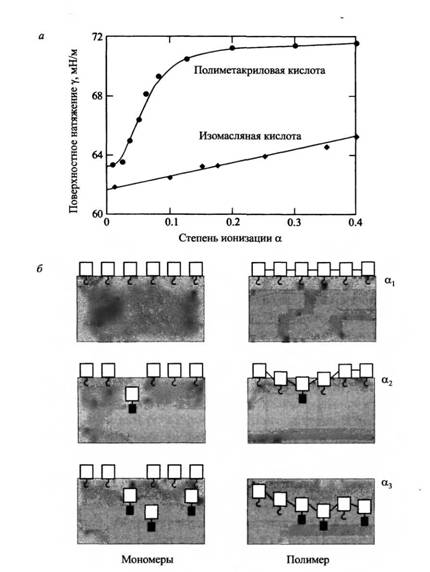
Рис.17. а - Зависимость поверхностного натяжения растворов полиметакриловой и изомасляной кислот от степени ионизации, б - Модель пробок, находящихся на поверхности, и прикрепленных к ним гирек, вызывающих десорбцию, которая иллюстрирует адсорбцию мономеров и полимеров на поверхности.