
Рефераты по рекламе
Рефераты по физике
Рефераты по философии
Рефераты по финансам
Рефераты по химии
Рефераты по хозяйственному праву
Рефераты по экологическому праву
Рефераты по экономико-математическому моделированию
Рефераты по экономической географии
Рефераты по экономической теории
Рефераты по этике
Рефераты по юриспруденции
Рефераты по языковедению
Рефераты по юридическим наукам
Рефераты по истории
Рефераты по компьютерным наукам
Рефераты по медицинским наукам
Рефераты по финансовым наукам
Рефераты по управленческим наукам
Психология педагогика
Промышленность производство
Биология и химия
Языкознание филология
Издательское дело и полиграфия
Рефераты по краеведению и этнографии
Рефераты по религии и мифологии
Рефераты по медицине
Шпаргалка: Физика, основы теории
Шпаргалка: Физика, основы теории
Механика. Молекулярная физика. Термодинамика
1. Основные понятия кинематики
Механика – это наука о движении и взаимодействии макроскопических тел.
Классическая механика состоит из трех частей: кинематики, динамики и статики.
Кинематика изучает движение тел, без учета причин, которыми обусловлено это движение.
Основными задачами кинематики являются:
1. Описание с помощью формул, таблиц и графиков совершаемых телом движений.
2. Определение кинематических величин, характеризующих это движение.
Для описания движений в кинематике вводится ряд специальных понятий (материальная точка, абсолютно твердое тело, система отсчета, траектория и т.д.) и величин (путь, перемещение, скорость, ускорение и т.д.)
Механическим движением называют изменение положения тела относительно других тел в пространстве с течением времени.
Тело, относительно которого рассматривается движение других тел, называется телом отсчета.
Систему координат и прибор для отсчета времени, связанные с телом отсчета, называют системой отсчета.
Тело, деформациями которого в данных условиях движения можно пренебречь, называют абсолютно твердым телом.
Тело, размерами которого в данных условиях движения можно пренебречь, называют материальной точкой.
Линию, описываемую материальной точкой при своем движении, называют траекторией.
Любое движение твердого тела можно разделить на два вида движения: поступательное и вращательное.
Поступательным называют такое движение, при котором любая прямая, связанная с движущимся телом, остается параллельной самой себе.
Вращательным называют такое движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения. (Ось вращения может находиться и вне тела).
2. Перемещение точки и пройденный путь. Скорость. Вычисление пройденного пути
Расстояние от точки А до точки В, отсчитанное вдоль траектории, называют пройденным путем. Иными словами, пройденный путь – это длина траектории, которую описывает материальная точка за данный промежуток времени.
Перемещением называют вектор,
соединяющий начальное положение материальной точки с её конечным положением ![]() .
.
Величины, для задания которых достаточно лишь численного значения, называются скалярами. (Примеры: путь, время, масса, работа, мощность и т.д.)
Величины, характеризующиеся численным значением и направлением, называются векторами. (Примеры: перемещение, скорость, ускорение, сила, импульс и т.д.)
Положение
материальной точки в пространстве можно задать при помощи радиуса-вектора ![]() .
.
Если
перемещение точки за время ![]() будет равно
будет равно ![]() , то под скоростью точки
в данный момент времени понимают предел, к которому стремится отношение
, то под скоростью точки
в данный момент времени понимают предел, к которому стремится отношение ![]() при
при ![]() (при
(при ![]() стремящемся к
нулю).
стремящемся к
нулю).
![]() =
=![]() .
.
Вектор скорости направлен по касательной к траектории в соответствующей точке.
При ![]()
![]() различия между
элементарным путем
различия между
элементарным путем ![]() и модулем элементарного
перемещения
и модулем элементарного
перемещения ![]() невелико,
поэтому
невелико,
поэтому ![]() ,
т.е.
,
т.е. ![]() .
.
Если задана зависимость скорости от времени, то пройденный путь можно найти, пользуясь формулой
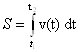
![]()
В случае
прямолинейного равномерного движения ![]()
![]() .
.
Прямолинейное равнопеременное движение. Ускорение. Физический смысл ускорения. Вычисление мгновенной скорости и пройденного пути при равнопеременном движении
Движение, при котором за любые равные промежутки времени скорость тела изменяется на одну и ту же величину, называется равнопеременным.
Быстрота изменения скорости материальной точки характеризуется ускорением
![]() , или
, или ![]() , т.е.
, т.е.![]() .
.
Физический смысл ускорения состоит в том, что оно является скоростью изменения скорости.
Если в
начальный момент времени скорость тела равна ![]() , то в любой момент времени t модуль
скорости тела
, то в любой момент времени t модуль
скорости тела
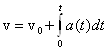 .
.
Если
ускорение постоянно, то модуль мгновенной скорости ![]()
Пройденный путь (при равнопеременном движении) можно найти по формуле:
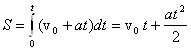 .
.
Для нахождения пройденного пути (в случае, если ускорение постоянно) также пользуются формулами:
![]() и
и ![]() .
.
3. Ускорение при криволинейном движении
Нормальное, тангенциальное и полное ускорение
В случае движения материальной точки по криволинейной траектории различают нормальное и тангенциальное ускорения.
Нормальное
(центростремительное) ускорение ![]() характеризует изменение скорости
по направлению. Оно направлено к центру кривизны траектории.
характеризует изменение скорости
по направлению. Оно направлено к центру кривизны траектории.
Модуль
нормального ускорения определяют по формуле ![]() , где R - радиус кривизны
траектории
, где R - радиус кривизны
траектории
Тангенциальное
(касательное) ускорение ![]() характеризует изменение скорости
по величине. Оно направлено по касательной к траектории.
характеризует изменение скорости
по величине. Оно направлено по касательной к траектории.
Модуль
тангенциального ускорения определяют по формуле ![]() .
.
Модуль
полного ускорения ![]() .
.
4. Кинематика вращательного движения
Тело, деформациями которого в данных условиях движения, можно пренебречь называют абсолютно твердым телом.
При
вращательном движении радиус-вектор каждой точки поворачивается за одно и то
время ![]() на
один и тот же угол
на
один и тот же угол ![]() .
.
![]() называют углом
поворота тела.
называют углом
поворота тела.
Угловой скоростью тела называют величину
![]() .
.
![]() - аксиальный
вектор (направлен вдоль оси вращения в сторону, определяемую правилом правого
винта).
- аксиальный
вектор (направлен вдоль оси вращения в сторону, определяемую правилом правого
винта).
Равномерное вращение характеризуется периодом обращения Т.
Периодом обращения называют промежуток времени, за которое тело делает один полный оборот (поворачивается на угол 2π).
Модуль угловой скорости равномерного движения
![]()
![]() .
.
Частотой
обращения называют число оборотов точки за единицу времени ![]() .
.
Таким
образом, ![]()
Угловое ускорение характеризует быстроту изменения угловой скорости (в случае неравномерного вращения)
![]() .
.
Линейная
скорость тела связана с угловой соотношением ![]() .
.
Модуль нормального ускорения
![]()
Модуль
тангенциального ускорения ![]() .
.
5. Первый закон Ньютона. Инерциальные системы отсчета. Принцип относительности Галилея
Раздел механики, изучающий причины, вызывающие ускорение и способы его вычисления, называют динамикой.
Динамика базируется на трёх законах Ньютона.
Согласно первому закону Ньютона, существуют такие системы отсчета, относительно которых поступательно движущееся тело сохраняет свою скорость постоянной, если на него не действуют другие тела или действия этих тел уравновешены.
Явление сохранения скорости тела при компенсации внешних воздействий на него называю инерцией. Поэтому первый закон Ньютона часто называют законом инерции.
Системы отсчета, в которых выполняется первый закон Ньютона, называются инерциальными. Если одна система отсчета, найденная с помощью опыта, инерциальна, то инерциальными будут и все другие, движущиеся относительно её равномерно и прямолинейно (т.е. без ускорения). Землю с большой степенью точности можно считать инерциальной системой отсчета.
Если рассматривать движение данного тела в нескольких инерциальных системах отсчета, то это движение отличается только скоростью, а ускорение тела во всех инерциальных системах отсчета одинаково. Это положение обобщено Галилеем и сформулировано им в виде принципа относительности в механике: во всех инерциальных системах отсчета при одинаковых начальных условиях все механические явления протекают одинаково, т.е. подчиняются одним законам.
Другими словами, все инерциальные системы отсчета равноправны - любую из них можно считать неподвижной, а остальные - движущимися относительно данной равномерно и прямолинейно.
Никакими механическими опытами, поставленными внутри инерциальной системы отсчета, невозможно установить, покоится эта система или движется равномерно и прямолинейно.
По отношению к различным инерциальным системам отсчета скорость движения тела относительна, а ускорение абсолютно.
Инерциальные системы отсчета играют в физике исключительно важную роль, так как, согласно принципу относительности Эйнштейна, математическое выражение любого закона физики имеет одинаковый вид в любой инерциальной системе отсчета.
6. Масса тела. Сила. Второй и третий законы Ньютона
Свойство тела сохранять свою скорость неизменной, т.е. сохранять состояние покоя или равномерного прямолинейного движения при отсутствии внешних воздействий на это тело или их взаимной компенсации, называют его инертностью. Инертность тел приводит к тому, что мгновенно изменить скорость тела невозможно - действие на него другого тела должно длиться определенное время. Чем инертнее тело, чем меньше изменяется его скорость за данное время, т.е. тем меньшее ускорение получает это тело.
Скорость тела может изменяться только непрерывно.
Масса тела является мерой инертности тела, а также источником и объектом тяготения.
Масса тела, являющаяся характеристикой его инерционных и гравитационных свойств, представляет собой величину, зависящую только от самого тела и не зависящую от того, в каких именно взаимодействиях с другими телами это тело участвует. Однако масса зависит от скорости движения тела. Эта зависимость обнаруживается только при движениях со скоростями, сравнимыми со скоростью света.
Массу тел определяют путем взвешивания на рычажных весах, кроме того, массу тела можно определить по взаимодействию этого тела с эталоном.
В СИ за единицу массы принимают килограмм (кг).
Действие одного тела на другое, в результате которого возникает ускорение тела или отдельных его частей, называется силой.
Причина ускорения тела - приложенная к нему сила.
Сила - векторная физическая величина. Действие силы на тело зависит от её модуля, направления и точки приложения.
Силу измеряют с помощью динамометров и пружинных весов.
Так как сила - величина векторная, то сложение сил производится по правилу сложения векторов.
Согласно
второму закону Ньютона, равнодействующая всех сил, приложенных к телу, равна
произведению массы тела на получаемое им ускорение: ![]() .
.
В СИ сила измеряется в ньютонах (Н).
Согласно
третьему закону Ньютона, силы, с которыми два тела действуют друг на друга,
направлены вдоль одной прямой, равны по модулю и противоположны по направлению:![]() .
.
Силы всегда появляются парами и внутри каждой пары они всегда одной природы.
Силы, возникающие при взаимодействии, тел никогда не уравновешивают друг друга, поскольку приложены к разным телам.
7. Сила тяжести. Вес тела. Перегрузки. Невесомость
Силу, с которой тело притягивается к Земле под действием поля тяготения Земли, называют силой тяжести. По закону всемирного тяготения на поверхности Земли (или вблизи этой поверхности) на тело массой m действует сила тяжести
![]() ,
,
где М – масса Земли; R – радиус Земли.
Если на тело действует только сила тяжести, то оно совершает свободное падение. Модуль ускорения свободного падения g находят по формуле
![]() .
.
Из данной формулы следует, что ускорение свободного падения не зависит от массы m падающего тела, т.е. для всех тел в данном месте Земли оно одинаково.
Модуль силы
тяжести можно определить по формуле ![]() . Эта сила имеет гравитационную
природу. Вектор силы тяжести приложен к центру тяжести тела.
. Эта сила имеет гравитационную
природу. Вектор силы тяжести приложен к центру тяжести тела.
Из закона всемирного
тяготения следует, что сила тяжести и вызываемое ею ускорение свободного
падения уменьшаются при увеличении расстояния от Земли. На высоте ![]() от поверхности
Земли модуль ускорения свободного падения определяют по формуле
от поверхности
Земли модуль ускорения свободного падения определяют по формуле
![]() .
.
Силу, с которой вследствие притяжения к Земле тело действует на свою опору или подвес, называют весом тела.
Вес тела является упругой силой, приложенной к опоре или подвесу (т.е. к связи).
Если тело
покоится или движется прямолинейно и равномерно, то его вес равен силе тяжести,
т.е. ![]() .
.
Если тело
движется ускоренно, то его вес зависит от этого ускорения и его направления
относительно направления вектора ускорения свободного падения.![]()
Если тело
движется с ускорением а, направленным вертикально вверх, то его вес ![]() Увеличение
веса тела, вызванное его ускоренным движением, называют перегрузкой.
Увеличение
веса тела, вызванное его ускоренным движением, называют перегрузкой.
Если тело
движется с ускорением а, направленным вертикально вниз (т.е. совпадающим
с направлением ускорения свободного падения), то его вес уменьшается. В этом
случае он определяется по формуле ![]()
При свободном
падении ![]()
![]() .
Следовательно, в данном случае
.
Следовательно, в данном случае ![]() , т.е вес отсутствует. Если тело
движется только под действием силы тяжести (свободно падает), то оно находится
в состоянии невесомости. Характерным признаком этого состояния является
отсутствие у свободно падающих тел деформаций и внутренних напряжений. Причина
невесомости тел заключается в том, что сила тяжести сообщает свободно падающему
телу и его опоре (или подвесу) одинаковые ускорения.
, т.е вес отсутствует. Если тело
движется только под действием силы тяжести (свободно падает), то оно находится
в состоянии невесомости. Характерным признаком этого состояния является
отсутствие у свободно падающих тел деформаций и внутренних напряжений. Причина
невесомости тел заключается в том, что сила тяжести сообщает свободно падающему
телу и его опоре (или подвесу) одинаковые ускорения.
8. Импульс тела. Импульс силы. Закон сохранения импульса
Уравнение
второго закона Ньютона можно представить в виде ![]() , или
, или ![]() .
.
Внеся ![]() под знак
дифференциала, получим
под знак
дифференциала, получим ![]() .
.
Векторную
величину, равную произведению массы тела на его скорость, называют импульсом
тела. Таким образом, импульс тела определяется по формуле ![]() . Следовательно,
. Следовательно, ![]() , т.е.
производная импульса материальной точки по времени равна равнодействующей всех
сил, приложенных к точке.
, т.е.
производная импульса материальной точки по времени равна равнодействующей всех
сил, приложенных к точке.
Последнюю
формулу можно представить в виде ![]() .
.
Приращение
импульса за время ![]() равно
равно
![]() =
=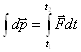 .
.
При ![]()
![]() =
=![]() . Величину
. Величину ![]() , равную
произведению силы на время её действия, называют импульсом силы.
, равную
произведению силы на время её действия, называют импульсом силы.
Изменение
импульса тела за время ![]() равно импульсу силы, действующей
на тело в течение этого времени.
равно импульсу силы, действующей
на тело в течение этого времени.
Рассмотрим систему, состоящую из N материальных точек (систему тел).
Силы, с которыми на данное тело действуют остальные тела системы, называют внутренними.
Силы, обусловленные воздействием тел, не принадлежащих системе, называют внешними.
В случае отсутствия внешних сил систему называют замкнутой.
Импульсом системы называют векторную сумму импульсов тел, образующих систему
![]() .
.
Группу тел,
взаимодействующих не только между собой, но и с телами, не входящими в состав
этой группы, называют незамкнутой системой. Силы, с которыми на тела данной системы
действуют тела, не входящие в эту систему, называю внешними (обычно внешние
силы обозначают буквой ![]() , а внутренние силы – буквой
, а внутренние силы – буквой ![]() .
.
Рассмотрим взаимодействие двух тел в незамкнутой системе. Изменение импульсов данных тел происходит как под действием внутренних сил, так и под действием внешних сил.
Согласно второму закону Ньютона, изменения импульсов рассматриваемых тел у первого и второго тел составляют
![]()
![]()
где t
– время действия внешних и внутренних сил. Почленно сложив данные выражения,
получим ![]() .
.
В этой
формуле ![]() -
полный импульс системы,
-
полный импульс системы,
![]() (согласно
третьему закону Ньютона),
(согласно
третьему закону Ньютона), ![]() - равнодействующая всех внешних
сил, действующих на тела данной системы. С учетом вышеизложенного получаем
формулу
- равнодействующая всех внешних
сил, действующих на тела данной системы. С учетом вышеизложенного получаем
формулу ![]() ,
из которой следует, что полный импульс системы изменяется только под
действием внешних сил. Если же система замкнутая, т.е.
,
из которой следует, что полный импульс системы изменяется только под
действием внешних сил. Если же система замкнутая, т.е. ![]() , то
, то ![]() и, следовательно,
и, следовательно, ![]() .
.
Закон сохранения импульса для замкнутой системы тел формулируется следующим образом: импульс замкнутой системы тел остается постоянным при любых взаимодействиях тел этой системы между собой.
На законе сохранения импульса основано реактивное движение.
9. Механическая работа и мощность
Если
действующая на тело сила ![]() вызывает его перемещение
вызывает его перемещение ![]() , то действие
силы характеризуется механической работой
, то действие
силы характеризуется механической работой
![]() , где
, где ![]() - угол между
направлением силы и перемещения. Формула справедлива для случая когда тело
движется прямолинейно и действующая на него сила остается постоянной. Если сила
изменяется, то
- угол между
направлением силы и перемещения. Формула справедлива для случая когда тело
движется прямолинейно и действующая на него сила остается постоянной. Если сила
изменяется, то ![]() .
.
Механическая работа является мерой изменения энергии. За единицу работы в системе Си принимают джоуль (Дж).
Средней
мощностью ![]() называют
величину, равную отношению работы
называют
величину, равную отношению работы ![]() к промежутку времени
к промежутку времени ![]() , за который
она совершается
, за который
она совершается
![]() .
.
Мгновенная
мощность определяется по формуле ![]() . Учитывая, что
. Учитывая, что ![]() , получаем
, получаем ![]() , где v
– мгновенная скорость.
, где v
– мгновенная скорость.
За единицу мощности в системе СИ принимают ватт (Вт).
На практике часто применяют внесистемную единицу мощности – лошадиную силу.
1 л.с. = 735 Вт
10. Кинетическая и потенциальная энергия
Физическая величина, характеризующая способность тела или системы тел совершать работу, называется энергией.
Энергия может быть обусловлена движением тела с некоторой скоростью (кинетическая энергия), а также нахождением тела в потенциальном поле сил (потенциальная энергия).
Кинетическая энергия
Рассмотрим
случай, когда тело массой m под действием силы F изменяет свою
скорость от ![]() до
до
![]() .
Определим работу силы, приложенной к телу
.
Определим работу силы, приложенной к телу
![]() .
.
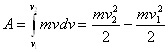 .
.
Так как
механическая работа является мерой изменения энергии, то величина ![]()
![]() представляет собой
энергию, обусловленную движением
представляет собой
энергию, обусловленную движением ![]() тела.
тела.![]()
Энергию,
которой обладает тело вследствие своего движения называют кинетической ![]() .
.
Работа совершаемая силой при изменении скорости тела, равна изменению кинетической энергии тела
![]()
Потенциальная энергия тела в поле силы тяжести
При падении
тела массой m с высоты ![]() до высоты
до высоты ![]() над Землей сила тяжести совершает
работу
над Землей сила тяжести совершает
работу
![]() или
или ![]() .
.
Сила тяжести является консервативной силой, а поле тяготения – потенциальным. Работа силы тяжести равна изменению потенциальной энергии тела, взятому с противоположным знаком
![]() .
.
Потенциальная
энергия тела в поле силы тяжести ![]() .
.
Энергия, которая определяется взаимным расположением тел или частей одного и того же тела называется потенциальной.
11. Закон сохранения полной механической энергии
Рассмотрим движение тела в замкнутой системе, в которой действуют только консервативные силы. Пусть, например, тело массой m свободно падает. При переходе тела из состояния 1 в состояние 2 сила тяжести совершает работу
![]() .
.
В то же время
![]() . Следовательно,
. Следовательно,
![]() .
Преобразовав данное выражение, получим
.
Преобразовав данное выражение, получим ![]() .
.
Сумма кинетической и потенциальной энергии тела называется полной механической энергией тела.
![]()
Согласно закону сохранения полной механической энергии: полная механическая энергия замкнутой системы тел, взаимодействующих друг с другом только консервативными силами, при любых движениях этих тел не изменяется. Происходят лишь взаимные превращения потенциальной энергии в кинетическую и обратно.
Системы, в которых сохраняется полная механическая энергия, называются консервативными.
Системы, в которых полная механическая энергия не сохраняется называются диссипативными (диссипация – переход энергии в другой вид, например, механической во внутреннюю).
В общем случае закон сохранения энергии в природе формулируется следующим образом:
Энергия тел никогда не исчезает и не появляется вновь: она лишь превращается из одного вида в другой или переходит от одного тела к другому.
![]()
12. Основные положения молекулярно-кинетической теории и их опытное обоснование. Масса и размеры молекул
Теорию, объясняющую строение и свойства тел на основе закономерностей движения и взаимодействия частиц, из которых состоят тела, называют молекулярно-кинетической.
Основные положения молекулярно-кинетической теории (МКТ) формулируются следующим образом:
1. Любое вещество имеет дискретное (прерывистое) строение. Оно состоит из отдельных частиц (молекул, атомов, ионов), разделенных промежутками.
2. Частицы находятся в состоянии непрерывного хаотического движения, называемого тепловым.
3. Частицы взаимодействуют друг с другом. В процессе их взаимодействия возникают силы притяжения и отталкивания.
Справедливость МКТ подтверждается многочисленными наблюдениями и фактами.
Наличие у веществ проницаемости, сжимаемости и растворимости свидетельствует о том, что они не сплошные, а состоят из отдельных, разделенных промежутками частиц. С помощью современных методов исследования (электронные и ионные микроскопы) получены изображения наиболее крупных молекул.
Броуновское движение и диффузия свидетельствуют о том, что частицы находятся в непрерывном движении.
Наличие прочности и упругости тел, явления смачивания, поверхностного натяжения в жидкостях и т.д. доказывают существование сил взаимодействия между молекулами.
Масса и размеры молекул.
Размер молекул является величиной условной. Его оценивают следующим образом. Между молекулами наряду с силами притяжения действуют и силы отталкивания, поэтому молекулы могут сближаться лишь до некоторого расстояния. Расстояние предельного сближения центров молекул называют эффективным диаметром молекулы. (При этом условно считают, что молекулы имеют сферическую форму.)
С помощью многочисленных методов определения масс и размеров молекул установлено, что за исключением молекул органических веществ, содержащих очень большое число атомов, большинство молекул по порядку величины имеют диаметр 1· 10 - 10 м и массу 1· 10 - 26 кг.
Относительная молекулярная масса.
Относительной молекулярной (или атомной) массой Мr (или Аr) называют величину, равную отношению массы молекулы (или атома) mо этого вещества к 1/12 массы атома углерода mоС, т.е.
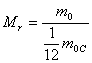
Относительная молекулярная (атомная) масса является величиной, не имеющей размерности.
Количество вещества. Молярная масса. Масса молекулы.
Количеством вещества ν называют величину, равную отношению числа молекул (или атомов) N в данном теле к числу атомов NA в 0,012 кг углерода, т.е. ν = N/ NA (NA - число Авогадро).
Молярной массой М какого-либо вещества называют массу 1 моль этого вещества.
М = mо NA
Следовательно, массу молекулы (атома) можно определить из соотношения
mо = М / NA
13. Идеальный газ. Основное уравнение МКТ идеального газа
Идеальным называют такой газ, при описании свойств которого делают следующие допущения: не учитывают собственный размер газовых молекул и не учитывают силы взаимодействия между ними.
Таким образом, моделью идеального газа является совокупность хаотически движущихся материальных точек, взаимодействующих между собой и со стенками содержащего газ сосуда только при непосредственном столкновении.
Основное уравнение МКТ идеального газа устанавливает зависимость между параметрами молекул и давлением. Давление газа возникает вследствие столкновений молекул со стенками сосуда, в котором находится газ.
Давление идеального газа
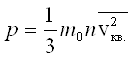
m0 –
масса молекулы; n – концентрация молекул, ![]()
![]() - квадрат средней квадратичной
скорости молекул.
- квадрат средней квадратичной
скорости молекул.![]()
![]()
![]() =
= 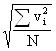
![]()
![]()
Формулу основного уравнения МКТ идеального газа можно представить в виде
![]() ,
,
где ![]()
![]() - средняя кинетическая
энергия поступательного движения молекул.
- средняя кинетическая
энергия поступательного движения молекул.
14. Абсолютная температура и её физический смысл
Уравнение состояния идеального газа (уравнение Менделеева-Клапейрона)
Под понятием «температура» подразумевают степень нагретости тела.
Существует несколько температурных шкал. В абсолютной (термодинамической) шкале температура измеряется в кельвинах (К). Нуль в этой шкале называют абсолютным нулем температуры, приблизительно равен - 2730С. при абсолютном нуле прекращается поступательное движение молекул.
Термодинамическая температура Т связана с температурой по шкале Цельсия следующим соотношением:
Т = (t0 + 273)K
Для идеального газа существует пропорциональная зависимость между абсолютной температурой газа и средней кинетической энергией поступательного движения молекул:
![]() ,
,
где k – постоянная Больцмана, k = 1,38· 10 – 23 Дж/К
Таким образом, абсолютная температура является мерой средней кинетической энергии поступательного движения молекул. В этом заключается её физический смысл.
Подставляя в
уравнение p = ![]() n
n![]() выражение для средней
кинетической энергии
выражение для средней
кинетической энергии
![]() =
= ![]() kT, получим
kT, получим
p = ![]() n ·
n · ![]() kT = nkT
kT = nkT
Из основного уравнения МКТ идеального газа p = nkT при подстановке
![]() ,
,
можно получить уравнение
![]() , или
, или ![]() A
· kT
A
· kT
NA·
k = R - универсальная
газовая постоянная, R = 8,31 ![]()
Уравнение ![]() называют
уравнением состояния идеального газа (уравнением Менделеева-Клапейрона).
называют
уравнением состояния идеального газа (уравнением Менделеева-Клапейрона).
15. Газовые законы. Графики изопроцессов.
1. Изотермический процесс (Т = const) подчиняется закону Бойля – Мариотта: для данной массы газа при постоянной температуре произведение давления на объём есть величина постоянная.
![]() , или
, или ![]() , или
, или ![]()
|
0 V |
Изотерма идеального газа в координатных осях P,V представлена на графике. |
2. Изобарный процесс (р = const) подчиняется закону Гей-Люссака: для данной массы газа при постоянном давлении отношение объема газа к абсолютной температуре есть величина постоянная.
![]() , или
, или ![]() , или
, или ![]()
|
0 T |
Изобара идеального газа в координатных осях V, T представлена на графике. |
3. Изохорный процесс (V = const) подчиняется закону Шарля: для данной массы газа при постоянном объеме отношение давления газа к абсолютной температуре есть величина постоянная.
![]() , или
, или ![]() или
или ![]()
|
0 T |
Изохора идеального газа в координатных осях P, T изображена на графике. |
Внутренняя энергия идеального газа. Способы изменения внутренней энергии.
Количество теплоты. Работа в термодинамике
Внутренней энергией называют сумму кинетической энергии хаотического движения молекул и потенциальной энергии их взаимодействия.
Так как молекулы идеального газа не взаимодействуют друг с другом, то внутренняя энергия U идеального газа равна сумме кинетических энергий хаотически движущихся молекул:
![]() , где
, где ![]() .
.
Таким образом,
![]()
![]() ,
,
где ![]() .
.
Для одноатомного газа i = 3, для двухатомного i = 5, для трех (и более)атомного i = 6.
Изменение внутренней энергии идеального газа
![]() .
.
Внутренняя энергия идеального газа является функцией его состояния. Внутреннюю энергию можно изменить двумя способами:
· путем теплообмена;
· путем совершения работы.
Процесс изменения внутренней энергии системы без совершения механической работы называют теплообменом или теплопередачей. Существуют три вида теплопередачи: теплопроводность, конвекция и излучение.
Количеством теплоты называют величину, являющуюся количественной мерой изменения внутренней энергии тела в процессе теплопередачи.
Количество теплоты, необходимое для нагревания (или отдаваемое телом при охлаждении) определяется по формуле:
![]() где с –
удельная теплоемкость вещества
где с –
удельная теплоемкость вещества
Работа в термодинамике
Элементарная
работа d A = p dV. При p = const 
16. Состояние системы. Процесс. Первый закон (первое начало) термодинамики
Системой тел называют совокупность рассматриваемых тел. Примером системы может быть жидкость и находящийся в равновесии с ней пар. В частности, система может состоять из одного тела.
Всякая система может находиться в различных состояниях, отличающихся температурой, давлением, объемом и т.д. Величины, характеризующие состояние системы, называют параметрами состояний.
Не всегда какой-либо параметр системы имеет определенное значение. Если, например, температура в разных точках тела неодинакова, то телу нельзя приписать определенное значение температуры. В этом случае состояние системы называют неравновесным.
Равновесным состоянием системы называют такое состояние, при котором все параметры системы имеют определенные значения, остающиеся при неизменных внешних условиях постоянными сколь угодно долго.
Процессом называют переход системы из одного состояния в другое.
Внутренняя энергия является функцией состояния системы. Это означает, что всякий раз, когда система оказывается в данном состоянии, её внутренняя энергия принимает присущее этому состоянию значение, независимо от предыстории системы. Изменение внутренней энергии системы при её переходе из одного состояния в другое (независимо от пути, по которому совершается переход) равно разности значений внутренней энергии в этих состояниях.
Согласно первому началу термодинамики количество теплоты, сообщенное системе, идет на приращение внутренней энергии системы и на совершение системой работы над внешними телами.
![]()
Применение первого закона термодинамики к процессам в газах. Адиабатный процесс.
1. Изотермический процесс (Т=const)
![]() , т.к.
, т.к. ![]() .
.
Работа газа в изотермическом процессе
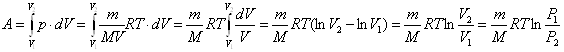 .
.
2. Изохорный процесс (V=const)
![]() , так как
, так как ![]() Следовательно
Следовательно ![]()
3. Изобарный процесс (p=const)
![]() .
.
4. Адиабатный процесс (Q = 0).
Адиабатным называют процесс, протекающий без теплообмена с окружающей средой.
Уравнение
адиабаты (уравнение Пуассона) имеет вид ![]() .
.
В
соответствии с первым законом термодинамики ![]() Следовательно,
Следовательно, ![]() .
.
При
адиабатном расширении ![]() , поэтому
, поэтому ![]() (газ охлаждается).
(газ охлаждается).
При
адиабатном сжатии ![]() , поэтому
, поэтому ![]() (газ нагревается). Адиабатное
сжатие воздуха применяют для воспламенения топлива в дизельных ДВС.
(газ нагревается). Адиабатное
сжатие воздуха применяют для воспламенения топлива в дизельных ДВС.
17. Тепловые двигатели
Под тепловым двигателем понимают устройство, преобразующее энергию сгоревшего топлива в механическую энергию. Тепловой двигатель, у которого рабочие части периодически возвращаются в исходное положение, называют периодическим тепловым двигателем.
К тепловым двигателям относятся:
· паровые машины,
· двигатели внутреннего сгорания (ДВС),
· реактивные двигатели,
· паровые и газовые турбины,
· холодильные машины.
Для работы периодического теплового двигателя необходимо выполнение следующих условий:
· наличие рабочего тела (пара или газа), которое, нагреваясь при сгорании топлива и расширяясь, способно совершить механическую работу;
· использование кругового процесса (цикла);
· наличие нагревателя и холодильника.
Второе начало термодинамики
Схема
теплового двигателя имеет вид, изображенный на рисунке. ![]() количество теплоты,
полученное рабочим телом от нагревателя,
количество теплоты,
полученное рабочим телом от нагревателя, ![]() - количество теплоты, отданное
рабочим телом холодильнику.
- количество теплоты, отданное
рабочим телом холодильнику.
Из схемы видно, что тепловой двигатель совершает работу только за счет передачи теплоты в одном направлении, а именно от более нагретых тел к менее нагретым, причем вся теплота, взятая от нагревателя, не может быть
превращена в механическую работу. Это не случайность, а результат объективных закономерностей, существующих в природе, которые отражены во втором начале термодинамики. Второе начало термодинамики показывает, в каком направлении могут протекать термодинамические процессы, и имеет несколько равнозначных формулировок. В частности, формулировка Кельвина такова: невозможен такой периодический процесс, единственным результатом которого является превращение теплоты, полученной от нагревателя, в эквивалентную ей работу.
КПД теплового двигателя. Цикл Карно.
Коэффициентом полезного действия (КПД) теплового двигателя называют величину, равную отношению количества теплоты, превращенной двигателем в механическую работу, к количеству теплоты, полученной от нагревателя:
![]()
КПД теплового двигателя всегда меньше единицы.
Для определения максимально возможного значения КПД теплового двигателя французский инженер С. Карно рассчитал идеальный обратимый цикл, состоящий из двух изотерм и двух адиабат. Он доказал, что максимальное значение КПД идеальной тепловой машины, работающей без потерь на обратимом цикле
![]() .
.
Любая
реальная тепловая машина, работающая с нагревателем при температуре ![]() и
холодильником при температуре
и
холодильником при температуре ![]() не может иметь КПД, превышающий
КПД идеальной тепловой машины с теми же температурами.
не может иметь КПД, превышающий
КПД идеальной тепловой машины с теми же температурами.
ЭЛЕКТРОМАГНЕТИЗМ
1. Электризация тел. Закон сохранения электрического заряда. Закон Кулона
Многие частицы и тела способны взаимодействовать между собой с силами, которые, как и силы тяготения пропорциональны квадрату расстояния между ними, но во много раз больше сил тяготения. Этот вид взаимодействия частиц называют электромагнитным.
Принято считать, что элементарные частицы, способные к электромагнитным взаимодействиям, имеют электрический заряд.
Следовательно, электрический заряд есть количественная мера способности частиц к электромагнитным взаимодействиям.
Существует два вида электрических заряда, условно называемых положительными и отрицательными. Одноименные заряды отталкиваются, а разноименные притягиваются.
Экспериментально установлено, что заряд любого тела состоит из целого числа элементарных зарядов, т.е. электрический заряд дискретен. Элементарный заряд обычно обозначают буквой е. Заряд всех элементарных частиц (если он не равен нулю) одинаков по абсолютной величине.
|e| = 1,6·10 –19 Кл
Любой заряд, больше элементарного, состоит из целого число элементарных зарядов
q = ± Ne (N = 1, 2, 3, …)
Электризация тел всегда сводится к перераспределению электронов. Если тело имеет избыток электронов, то оно заряжено отрицательно, если - недостаток электронов, то тело заряжено положительно.
В изолированной системе алгебраическая сумма электрических зарядов остается постоянной (закон сохранения электрического заряда):
q1 + q2 +…+ qN = ∑qi = const
Закон, которому подчиняется сила взаимодействия точечных неподвижных зарядов установлен Кулоном (1785 г.)
Точечным зарядом называют заряженное тело, размерами которого можно пренебречь по сравнению с расстояниями от этого тела до других тел, несущих электрический заряд.
Согласно закону Кулона сила взаимодействия двух неподвижных точечных зарядов в вакууме прямо пропорциональна произведению модулей зарядов и обратно пропорциональна квадрату расстояния между ними.
| F = k |
|q1| ·|q2| |
|
r2 |
k – коэффициент пропорциональности.
| В СИ k = | 1 |
|
4πε0 |
k = 9·109 Н·м2/Кл2 ε0 = 8,85·10-12 Кл2/Н·м2 (ε0 – электрическая постоянная).
2. Электрическое поле. Напряженность электрического поля. Принцип суперпозиции электрических полей
Электрическое поле – вид материи, посредством которого происходит взаимодействие электрических зарядов.
Силовой характеристикой электрического поля является напряженность электрического поля.
Напряженность электрического поля в данной точке равна отношению силы, с которой поле действует на пробный заряд, помещенный в данную точку поля, к величине этого заряда.
![]() .
.
Напряженность электрического поля измеряется в ![]() или в
или в ![]() .
.
Напряженность поля точечного заряда ![]() .
.
Согласно принципу суперпозиции (наложения) полей напряженность поля системы зарядов равна векторной сумме напряженностей полей, которые создавал бы каждый из зарядов системы в отдельности.
|
|
|
Электрические поля могут быть изображены графически с помощью линий напряженности (силовых линий) электрического поля.
Линией напряженности электрического поля называют линию, касательная к которой в каждой точке совпадает с направлением вектора напряженности в этой точке.
|
|
Густота линий выбирается так, чтобы количество линий,
пронизывающих единицу площади поверхности, перпендикулярной к линиям площадки
было равно численному значению вектора |
3. Работа сил электростатического поля. Потенциал электростатического поля
|
dr α dl 1 q´ 2
r1 r2
|
Сила, действующая на
точечный заряд, находящийся в поле другого заряда, является центральной.
Центральное поле сил является потенциальным. Если поле потенциально, то
работа по перемещению заряда в этом поле не зависит от пути, по которому
перемещается заряд Работа на элементарном пути
|
![]() =
= 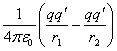 .
.
Из данной формулы следует, что силы, действующие на заряд ![]() в поле неподвижного
заряда
в поле неподвижного
заряда ![]() ,
являются консервативными, т.к. работа по перемещению заряда
,
являются консервативными, т.к. работа по перемещению заряда ![]() действительно
определяется начальным и конечным положением заряда.
действительно
определяется начальным и конечным положением заряда.
Из курса механики известно, что работа консервативных сил на замкнутом пути равна нулю.
|
|
Циркуляция вектора напряженности электростатического поля по любому замкнутому контуру равна нулю. |
Потенциал
Тело, находящееся в потенциальном поле сил, обладает энергией, за счет которой совершается работа силами поля
![]() .
.
Следовательно, потенциальная энергия заряда ![]() в поле неподвижного заряда
в поле неподвижного заряда ![]()
![]() .
.
Величина, равная отношению потенциальной энергии заряда к величине этого заряда, называется потенциалом электростатического поля
![]() .
.
Потенциал является энергетической характеристикой электрического поля.
Потенциал электрического поля точечного заряда
![]() .
.
Потенциал поля, создаваемого системой заряженных тел равен алгебраической сумме потенциалов, создаваемых каждым зарядом в отдельности
![]() .
.
Заряд ![]() ,
находящийся в точке поля с потенциалом
,
находящийся в точке поля с потенциалом ![]() , обладает энергией
, обладает энергией
![]()
![]() .
.
Работа сил поля над зарядом ![]()
Величина ![]() называется напряжением. Потенциал
и разность потенциалов (напряжение) измеряются в вольтах (В).
называется напряжением. Потенциал
и разность потенциалов (напряжение) измеряются в вольтах (В).
4. Связь между напряженностью электростатического поля и потенциалом
Работа сил электрического поля над зарядом ![]() на отрезке пути
на отрезке пути ![]()
![]() .
.
С другой стороны ![]() , поэтому
, поэтому ![]() .
.
Отсюда следует, что
![]() .
. ![]() ;
; ![]() ;
; ![]() .
.
![]() .
.
![]() .
.
Величина, стоящая в скобках, называется градиентом потенциала.
Следовательно, напряженность электрического поля равна градиенту
потенциала, взятому с противоположным знаком ![]() .
.
Для однородного электростатического поля ![]() , в то же время
, в то же время ![]() . Следовательно,
. Следовательно, ![]() ,
, ![]() .
.
Для наглядного изображения электрического поля наряду с линиями напряженности пользуются поверхностями равного потенциала (эквипотенциальными поверхностями). Линии напряженности электростатического поля перпендикулярны (ортогональны) эквипотенциальным поверхностям.
![]()
5. Проводники в электростатическом поле. Явление электростатической
индукции. Диэлектрики в электростатическом поле
Проводники в электростатическом поле. Электростатическая индукция.
К проводникам относят вещества, у которых имеются свободные заряженные частицы, способные двигаться упорядоченно по всему объему тела под действием электрического поля. Заряды таких частиц называют свободными.
Проводниками являются металлы, некоторые химические соединения, водные растворы солей, кислот и щелочей, расплавы солей, ионизированные газы.
Рассмотрим поведение в электрическом поле твердых металлических проводников. В металлах носителями свободных зарядов являются свободные электроны, называемые электронами проводимости.
|
+σ Е0 -σ - + - + - + - + - + - + |
Если внести незаряженный металлический проводник в однородное электрическое поле, то под действием поля в проводнике возникает направленное движение свободных электронов в направлении, противоположном направлению вектора напряженности Ео этого поля. Электроны будут скапливаться на одной стороне проводника, образуя там избыточный отрицательный заряд, а их недостача на другой стороне проводника приведет к образованию там избыточного положительного заряда, т.е. в проводнике произойдет разделение зарядов. Эти нескомпенсированные разноименные заряды появляются на проводнике только под действием внешнего электрического поля, т.е. такие заряды являются индуцированными (наведенными), а в целом проводник по-прежнему остается незаряженным. |
Такой вид электризации, при котором под действием внешнего электрического поля происходит перераспределение зарядов между частями данного тела, называют электростатической индукцией.
Появившиеся вследствие электростатической индукции на противоположных частях проводника нескомпенсированные электрические заряды создают своё собственное электрическое поле, его напряженность Ес внутри проводника направлена против напряженности Ео внешнего поля, в которое помещен проводник. По мере разделения зарядов в проводнике и накопления их на противоположных частях проводника напряженность Ес внутреннего поля увеличивается и становится равной Ео. Это приводит к тому, что напряженность Е результирующего поля внутри проводника становится равной нулю. При этом наступает равновесие зарядов на проводнике.
Весь нескомпенсированный заряд в этом случае находится только на наружной поверхности проводника, а внутри проводника электрическое поле отсутствует.
Данное явление используют при создании электростатической защиты, сущность которой состоит в том, что для предохранения чувствительных приборов от влияния электрических полей их помещают в металлические заземленные корпуса или сетки.
Диэлектрики в электростатическом поле.
К диэлектрикам относят вещества, в которых при обычных условиях (т.е. при не слишком высоких температурах и отсутствии сильных электрических полей) нет свободных электрических зарядов.
В отличие от проводников в диэлектриках заряженные частицы не способны двигаться по всему объему тела, а могут лишь смещаться на небольшие расстояния (порядка атомных) относительно своих постоянных положений. Следовательно, электрические заряды в диэлектриках являются связанными.
В зависимости от строения молекул все диэлектрики можно разбить на три группы. К первой группе относятся диэлектрики, молекулы которых имеют асимметричное строение (вода, спирты, нитробензол). У таких молекул центры распределения положительных и отрицательных зарядов не совпадают. Такие молекулы можно рассматривать как электрические диполи.
Молекулы, представляющие собой электрические диполи называю полярными. Они обладают электрическим моментом p = q l даже при отсутствии внешнего поля.
Ко второй группе относят диэлектрики, молекулы которых симметричны (например, парафин, азот, кислород). У таких молекул центры распределения положительных и отрицательных зарядов совпадают. При отсутствии внешнего электрического поля такие молекулы не обладают электрическим моментом. Их называют неполярными молекулами.
Во внешнем электрическом поле центры распределения положительных и отрицательных зарядов неполярных молекул смещаются в противоположные стороны. Молекулы становятся диполями и приобретают дополнительный электрический момент p = q l.
К третьей группе относят кристаллические диэлектрики, имеющие ионное строение (NaCl, CaCl2 и другие).
|
F+ +q
α Е0
-q F- |
Поскольку молекулы и полярных и неполярных диэлектриков в электрическом поле представляют собой электрические диполи, рассмотрим поведение диполя во внешнем однородном поле (Ео = соnst). На каждый из зарядов диполя действует сила. Эти силы F+ и F- равны по модулю и противоположны по направлению. Они создают пару сил, создающих вращательный момент М = рЕо sin α. Под действием вращательного момента М диполь стремится повернуться так, чтобы направление вектора р совпало с направлением вектора Ео, т.е. ориентируется по направлению внешнего поля. |
Если диэлектрик неполярный, то при отсутствии внешнего электрического поля его молекулы вообще не имеют электрических моментов. Если же диэлектрик полярный, но не находится в электрическом поле, то тепловое движение создает полный беспорядок в расположении его молекул-диполей, вследствие чего их электрические моменты ориентированы по всевозможным направлениям и их векторная сумма равна нулю. Следовательно, диэлектрик в целом не обладает электрическим моментом.
|
-σ´ Е0 +σ´ -σ |
Пусть образец из диэлектрика находится в однородном электрическом поле. Поскольку молекулы и полярных и неполярных диэлектриков в электрическом поле являются диполями, а диполи ориентируются вдоль внешнего поля, векторы электрических моментов молекул в основном ориентированы упорядоченно. В этом случае векторная сумма электрических моментов не равна нулю. Следовательно, диэлектрик в целом обладает электрическим моментом. Внутри диэлектрика, находящегося в электрическом поле, разноименные заряды соседних диполей расположены вблизи друг друга и взаимно компенсируются. Поэтому диэлектрик остается незаряженным. А на противоположных поверхностях диэлектрика, | |||||||||||
перпендикулярных линиям напряженности внешнего поля, появляются нескомпенсированные и равные по значению поляризационные заряды, т.е. диэлектрик поляризуется.
Если в электрическое поле внести диэлектрик ионного типа, то в нем происходит небольшое смещение ионов кристаллической решетки (положительных - по полю, отрицательных - против поля). Это приводит к тому, что ионный диэлектрик в электрическом поле обладает электрическим моментом.
Таким образом, сущность процесса поляризации диэлектрика любого типа состоит в том, что в электрическом поле каждый элемент объема диэлектрика и весь диэлектрик в целом приобретает отличный от нуля электрический момент.
Поляризационные заряды создают в диэлектрике собственное электрическое поле, направленное против внешнего электрического поля. В результате суперпозиции двух этих полей напряженность поля, создаваемого зарядами, внесенными в диэлектрик, становится в нем в ε раз меньше, чем в вакууме (ε - диэлектрическая проницаемость среды).
6. Электроемкость. Конденсаторы. Емкость плоского конденсатора
Потенциал уединенного проводника пропорционален сообщенному ему заряду, поэтому отношение заряда проводника к его потенциалу не зависит от заряда и является характеристикой данного проводника.
Электроемкостью уединенного проводника называют величину, равную отношению заряда проводника к потенциалу этого проводника.
![]()
![]()
![]() .
.
На практике
применяются ![]()
Электроемкость проводника не зависит от вещества, из которого он изготовлен, а зависит от его формы, размеров и диэлектрической проницаемости среды, в которой находится этот проводник.
Используя формулу потенциала электрического поля, созданного равномерно заряженным шаром
![]() , для емкости
шара получим
, для емкости
шара получим 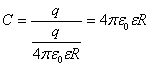 .
.
КОНДЕНСАТОРЫ
Уединенные проводники обладают малой емкостью. На практике возникает потребность в устройствах, которые при небольшом относительно окружающих тел потенциале накапливали бы на себе значительные заряды.
Конденсатором называют систему, состоящую из двух разделенных диэлектриком проводников, на которых могут накапливаться заряды противоположных знаков.
Проводники, образующие конденсатор, называют обкладками.
Чтобы внешние тела не влияли на емкость конденсатора, обкладкам придают такую форму и так располагают их друг относительно друга, чтобы поле, создаваемое накапливаемыми на них зарядами, было полностью сосредоточено внутри конденсатора. Этому условию удовлетворяют две близко расположенные пластины, два коаксиальных цилиндра и две концентрические сферы.
Емкостью конденсатора называют величину, равную отношению заряда конденсатора к разности потенциалов (напряжению) между его обкладками
![]() =
=![]() .
.
ЕМКОСТЬ ПЛОСКОГО КОНДЕНСАТОРА
Напряженность поля между обкладками плоского конденсатора
![]() .
.
Для однородного поля справедливо соотношение
![]() .
.
Следовательно, емкость плоского конденсатора
![]()
(S – площадь обкладок, d – расстояние между обкладками).
7. Соединение конденсаторов. Энергия заряженного конденсатора
При параллельном соединении конденсаторов напряжения на каждом конденсаторе одинаковы и равны напряжению на клеммах батареи
![]() .
.
Заряд батареи
![]() .
.
Исходя из того, что ![]() , имеем
, имеем
![]() ,
,
поэтому
![]() .
.
При последовательном соединении конденсаторов
![]() ,
, ![]() .
.
Учитывая, что ![]() , имеем
, имеем
![]() ,
,
поэтому при последовательном соединении конденсаторов
![]() .
.
ЭНЕРГИЯ ЗАРЯЖЕННОГО КОНДЕНСАТОРА
При зарядке конденсатора совершается работа по перемещению электрических
зарядов против сил электрического поля. При перемещении заряда ![]() совершается работа
совершается работа ![]() . Учитывая, что
. Учитывая, что
![]() , получим
, получим ![]() .
Следовательно,
.
Следовательно,
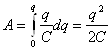 .
.
По закону сохранения энергии эта работа равна энергии заряженного конденсатора, т.е.
![]() .
.
Используя формулы ![]() и
и ![]() , получим
, получим
![]() и
и ![]() .
.
8. Закон Ома для однородного участка цепи. Сопротивление проводников
Участок цепи, на котором не действуют сторонние силы, приводящие к возникновению ЭДС, называется однородным.
Согласно закону Ома для однородного участка цепи постоянного тока: сила тока в однородном проводнике пропорциональна напряжению на его концах и обратно пропорциональна сопротивлению данного проводника.
![]() .
.
Опыты показывают, что сопротивление R проводника пропорционально его длине, обратно пропорционально площади его поперечного сечения и зависит от вещества, из которого изготовлен проводник. Для однородного проводника длиной l и неизменной площадью поперечного сечения S эту зависимость выражают формулой
![]() ,
,
где ![]()
![]() - коэффициент
пропорциональности, называемый удельным электрическим сопротивлением. Удельное
сопротивление равно сопротивлению проводника, изготовленного из данного
вещества и имеющего единичную длину и единичную площадь поперечного сечения.
Удельное сопротивление есть свойство проводника и зависит от его состояния.
- коэффициент
пропорциональности, называемый удельным электрическим сопротивлением. Удельное
сопротивление равно сопротивлению проводника, изготовленного из данного
вещества и имеющего единичную длину и единичную площадь поперечного сечения.
Удельное сопротивление есть свойство проводника и зависит от его состояния.
Сопротивление цепи, состоящей из последовательно соединенных проводников, равно сумме сопротивлений этих проводников.
![]() .
.
Сопротивление цепи, состоящей из параллельно соединенных проводников можно определить из формулы
![]()
9. Закон Джоуля - Ленца. Закон Ома для неоднородного участка цепи. Разветвленные цепи. Правила Кирхгофа
В замкнутой электрической цепи, по которой идет ток, происходят процессы превращения энергии из одного вида в другой. В источнике тока не электрическая энергия превращается в электрическую, а на потребителях энергии, включенных во внешнюю часть цепи, энергия электрического тока может превращаться в любой другой вид энергии (в зависимости от типа потребителя).
Если движущихся проводников на данном участке цепи нет, энергия электрического тока переходит во внутреннюю энергию этого участка, увеличивая её. Если участок однородный, то увеличение его внутренней энергии приводит к повышению температуры участка. Проводник, по которому идет ток, нагревается и отдает теплоту окружающим телам. Закон, определяющий количество теплоты, выделяемое в проводнике, был установлен экспериментально Джоулем и Ленцем. Согласно закону Джоуля - Ленца, количество теплоты, выделившееся при прохождении по нему тока, пропорционально квадрату силы тока, сопротивлению проводника и времени, в течение которого в проводнике поддерживается постоянный ток.
Формула
закона Джоуля – Ленца имеет следующий вид ![]() .
.
Постоянный ток в замкнутой цепи вызывается стационарным электрическим полем, которое должно непрерывно поддерживаться источником тока. В источнике тока действуют не электростатические силы, называемые сторонними. Эти силы совершают работу против электростатических сил по разделению положительных и отрицательных зарядов, что и приводит к поддержанию электрического поля в цепи и разности потенциалов между любыми её точками. Работа сторонних сил связана с превращением энергии не электрической в энергию электрического тока. Количественной мерой работы сторонних сил является величина, называемая электродвижущей силой (ЭДС).
ЭДС источника равна отношению работы сторонних сил, совершаемой при перемещении по замкнутой цепи заряда к величине этого заряда, т.е.
![]()
ЭДС выражают в вольтах (В).
Сторонние силы могут действовать не только в источнике тока, но и на отдельных участках цепи. Такие участки называют неоднородными. ЭДС неоднородного участка цепи численно равна работе сторонних сил при перемещении единичного заряда по данному участку.
Согласно закону Ома для неоднородного участка цепи
![]() .
.
В этой
формуле ![]()
![]() - ЭДС,
действующая на данном неоднородном участке,
- ЭДС,
действующая на данном неоднородном участке,
![]() - разность
потенциалов между концами участка,
- разность
потенциалов между концами участка, ![]() - полное сопротивление участка
(равно сумме внешнего и внутреннего сопротивления).
- полное сопротивление участка
(равно сумме внешнего и внутреннего сопротивления).
В случае замкнутой цепи закон Ома имеет следующий вид:
![]() .
.
Для расчета разветвленных цепей постоянного тока используют законы (правила) Кирхгофа.
Если считать токи, входящие в узел, положительными, а выходящие из узла – отрицательными, то первое правило Кирхгофа может быть сформулировано так:
в любом узле замкнутой электрической цепи алгебраическая сумма токов равна нулю, т.е.
![]() .
.
Второе правило Кирхгофа является обобщением закона Ома на разветвленные цепи и может быть сформулировано так: в любом неразветвленном контуре алгебраическая сумма ЭДС равна алгебраической сумме падений напряжений, т.е.
![]() .
.
На основе правил Кирхгофа составляют систему уравнений, решение которой позволяет вычислить силы токов в ветвях цепи.
10. Взаимодействие токов. Магнитное поле. Магнитная индукция
Если по двум тонким прямолинейным проводникам текут токи одного направления, то проводники притягиваются, если направления токов противоположны, то проводники отталкиваются.
Сила взаимодействия для прямолинейных проводников, приходящаяся на единицу длины, определяется по формуле:
![]() ,
,
где а
– расстояние между проводниками, ![]() - магнитная постоянная,
- магнитная постоянная, ![]() .
.
Взаимодействие токов, осуществляется посредством магнитных полей создаваемых токами.
Подобно тому,
как для исследования электростатического поля используют пробный точечный
заряд, для исследования магнитного поля используют пробный ток, циркулирующий в
пробном замкнутом контуре очень малых размеров. Ориентацию контура в
пространстве характеризуют направлением нормали ![]() к контуру, связанной с
направлением тока правилом правого винта. Такую нормаль называют положительной.
к контуру, связанной с
направлением тока правилом правого винта. Такую нормаль называют положительной.
Если внести пробный контур в магнитное поле, то поле оказывает на контур ориентирующее действие, устанавливая его положительной нормалью в определенном направлении. Это направление принимают за направление магнитного поля в данной точке.
Магнитным моментом контура называют величину
![]() ,
,
где I – сила тока в контуре, S – площадь контура.
Физическую
величину, равную отношению максимального вращательного момента ![]() , действующего на
контур, к магнитному моменту контура называют магнитной индукцией
, действующего на
контур, к магнитному моменту контура называют магнитной индукцией
![]()
Магнитная индукция в системе СИ измеряется в теслах (Тл).
Наряду с магнитной индукцией для описания магнитного поля вводится величина, называемая напряженностью магнитного поля. Для вакуума
![]() .
.
11. Магнитное поле в веществе. Магнитные свойства вещества
Гипотеза Ампера
Если
проводники, по которым течет ток, находятся не в вакууме, а в среде, то
магнитное поле может существенно изменяться. Это обусловлено тем, что всякое
вещество является магнетиком, т.е. способно намагничиваться. Намагниченное
вещество создает магнитное поле ![]() , которое накладывается на поле
, которое накладывается на поле ![]() , обусловленное
токами. Индукция результирующего поля:
, обусловленное
токами. Индукция результирующего поля: ![]() .
.
Причина магнитных свойств вещества была объяснена Ампером. Он пришел к выводу, что магнитные свойства любого тела определяются замкнутыми электрическими токами внутри него. Согласно гипотезе Ампера внутри молекул и атомов циркулируют элементарные электрические токи. Если плоскости, в которых циркулируют эти токи, расположены хаотично вследствие теплового движения молекул, то вещество не обнаруживает магнитных свойств. Если вещество намагничено, то токи ориентированы так, что их действия складываются.
Магнитные свойства вещества
Намагничение
магнетика характеризуют магнитным моментом единицы объема. Эту величину
называют вектором намагничения ![]()
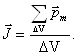
Формула справедлива для неоднородно намагниченного магнетика.
![]() - бесконечно
малый объем, взятый в окрестности рассматриваемой точки,
- бесконечно
малый объем, взятый в окрестности рассматриваемой точки,
![]() - магнитный
момент отдельной молекулы. Суммирование производится по всем молекулам,
заключенным в объеме
- магнитный
момент отдельной молекулы. Суммирование производится по всем молекулам,
заключенным в объеме ![]() .
.
Вектор
намагничения связан с напряженностью магнитного поля в той же точке
соотношением ![]() , где
, где ![]() - магнитная восприимчивость
вещества (безразмерная величина).
- магнитная восприимчивость
вещества (безразмерная величина).
Часто вместо
восприимчивости единицы объема ![]() пользуются отнесенной к одному
киломолю вещества киломолярной (для химически простых веществ – килоатомной)
восприимчивостью
пользуются отнесенной к одному
киломолю вещества киломолярной (для химически простых веществ – килоатомной)
восприимчивостью ![]() .
.
![]() , где
, где ![]() - объем
киломоля вещества (измеряется в
- объем
киломоля вещества (измеряется в ![]() ).
).
В зависимости от знака и величины магнитной восприимчивости все магнетики подразделяются на три группы:
1)
диамагнетики,
у которых ![]() -
отрицательна и мала по абсолютной величине (
-
отрицательна и мала по абсолютной величине (![]() ~
~ ![]() ).
).
2)
парамагнетики,
у которых ![]() тоже
невелика, но положительна (
тоже
невелика, но положительна (![]() ~
~ ![]() ).
).
3)
Ферромагнетики,
у которых ![]() положительна
и достигает больших значений (
положительна
и достигает больших значений (![]() ~
~ ![]() ).
).
Кроме того, в
отличие от диа- и парамагнетиков, для которых ![]() постоянна, магнитная
восприимчивость ферромагнетиков является функцией напряженности магнитного
поля.
постоянна, магнитная
восприимчивость ферромагнетиков является функцией напряженности магнитного
поля.
Таким
образом, вектор намагничения ![]() может как совпадать по
направлению с
может как совпадать по
направлению с ![]() (у пара- и ферромагнетиков), так
и быть направленным в противоположную сторону (у диамагнетиков).
(у пара- и ферромагнетиков), так
и быть направленным в противоположную сторону (у диамагнетиков).
Описание поля в магнетиках
Для описания поля в магнетиках часто пользуются величиной
![]() .
.
![]() напряженность
магнитного поля.
напряженность
магнитного поля.
В вакууме
вектор намагничения ![]() , поэтому
, поэтому ![]()
![]() .
.
В магнетиках ![]() , или
, или ![]() .
.
Величину ![]() называют
относительной магнитной проницаемостью вещества.
называют
относительной магнитной проницаемостью вещества.
Следовательно,
![]() .
.
ДИАМАГНЕТИКИ
У
диамагнетиков магнитная проницаемость ![]() чуть меньше единицы. К ним
относят, например, медь, золото, серебро, ртуть, хлор, инертные газы и другие
вещества.
чуть меньше единицы. К ним
относят, например, медь, золото, серебро, ртуть, хлор, инертные газы и другие
вещества.
Образец из диамагнитного материала, помещенный во внешнее однородное магнитное поле, устанавливается перпендикулярно линиям индукции этого поля. В неоднородном магнитном поле на образец действует сила, стремящаяся вытолкнуть его за пределы поля. Магнитная проницаемость диамагнетиков не зависит от напряженности магнитного поля.
Атомы
диамагнитных веществ не обладают магнитным моментом (векторная сумма
орбитальных и спиновых магнитных моментов электронов атома равна нулю). Когда
диамагнетик попадает во внешнее магнитное поле, то под действием этого поля у
атомов диамагнетика индуцируются магнитные моменты, ориентированные против
направления внешнего поля. В результате модуль магнитной индукции результирующего
поля В меньше, чем модуль индукции магнитного поля в вакууме ![]() .
.
ПАРАМАГНЕТИКИ
У
парамагнетиков ![]() чуть больше единицы. К ним
относят натрий, магний, алюминий, кислород, многие другие элементы, а так же
растворы некоторых солей.
чуть больше единицы. К ним
относят натрий, магний, алюминий, кислород, многие другие элементы, а так же
растворы некоторых солей.
Образец из парамагнетика в однородном внешнем магнитном поле устанавливается вдоль линий индукции поля. В неоднородном магнитном поле на парамагнитный образец действует сила, стремящаяся втянуть его в область более сильного поля. Магнитная проницаемость парамагнетиков не зависит от напряженности внешнего магнитного поля.
Парамагнитные вещества состоят из атомов, в которых орбитальные магнитные моменты электронов нескомпенсированы. Поэтому атомы парамагнетика имеют отличные от нуля магнитные моменты. Однако при отсутствии внешнего магнитного поля тепловое движение атомов приводит к хаотическому расположению их магнитных моментов, вследствие чего любой объем парамагнетика в целом магнитным моментом не обладает.
При внесении парамагнетика во внешнее магнитное поле его атомы в большей или меньшей степени (в зависимости от индукции поля) располагаются так, что их магнитные моменты ориентируются по направлению внешнего поля. В результате индукция результирующего поля в парамагнетике больше индукции магнитного поля в вакууме, т.е. В>В0.
12. Закон Ампера. Сила Лоренца
Ампер
экспериментально установил, что величина силы, действующей на элемент тока ![]() , находящийся в
магнитном поле с индукцией В определяется по формуле
, находящийся в
магнитном поле с индукцией В определяется по формуле
![]() ,
,
где ![]() - угол между
векторами
- угол между
векторами ![]() и
и
![]() (
(![]() направлен по
току в проводнике).
направлен по
току в проводнике).
Для прямолинейного проводника формула модуля силы Ампера имеет вид
![]() .
.
Направление силы Ампера определяют по правилу левой руки. Сила Ампера всегда перпендикулярна элементу тока и направлению вектора магнитной индукции.
Действие магнитного поля на проводник с током используется в устройстве электродвигателей, громкоговорителей, электроизмерительных приборов магнитоэлектрической системы.
На заряженную частицу, движущуюся в магнитном поле, действует сила Лоренца
![]() ,
,
где q
– заряд частицы, v- её скорость, ![]() - угол между векторами
- угол между векторами ![]() и
и ![]() .
.
Направление силы Лоренца определяют по правилу левой руки. Сила Лоренца всегда перпендикулярна направлению вектора скорости и вектора магнитной индукции. Под действием этой силы модуль скорости заряда и его кинетическая энергия не изменяются, а направление скорости заряда изменяется непрерывно.
Действие магнитного поля на движущиеся заряды широко используют в технике. Например, с помощью магнитного поля осуществляют фокусировку пучков заряженных частиц в ряде электронных приборов, управление электронным лучом в кинескопах телевизоров.
В экспериментальных установках для осуществления управляемой термоядерной реакции действие магнитного поля на плазму используют для скручивания её в шнур, не касающийся стенок рабочей камеры.
Движение заряженных частиц в магнитном поле по окружности используют в циклических ускорителях заряженных частиц – циклотронах.
Действие силы Лоренца применяют также в масс-спектрографах, которые предназначены для разделения заряженных частиц по их удельным зарядам.
13. Ферромагнетики. Магнитный гистерезис. Применения ферромагнетизма. Природа ферромагнетизма
Вещества, у которых магнитная проницаемость во много раз больше единицы, называют ферромагнетиками. К ним относят железо, никель, кобальт и многие сплавы.
Во внешнем
магнитном поле ферромагнитный образец ведет себя подобно парамагнитному. Однако
магнитная проницаемость ферромагнетика зависит от напряженности внешнего
магнитного поля и изменяется в довольно широких пределах, вследствие чего
зависимость ![]() является
нелинейной. Впервые зависимость
является
нелинейной. Впервые зависимость ![]() от Н экспериментально
исследовал А.Г. Столетов.
от Н экспериментально
исследовал А.Г. Столетов.
Значение магнитной проницаемости у некоторых ферромагнитных сплавов достигает десятков тысяч. Поэтому ферромагнетики относят к сильномагнитным веществам.
Для каждого ферромагнетика существует определенная температура, называемая точкой Кюри, при нагревании выше которой данное вещество теряет ферромагнитные свойства и превращается в парамагнетик (для железа 1043 К, для никеля 631 К).
МАГНИТНЫЙ ГИСТЕРЕЗИС
Явление запаздывания изменения магнитной индукции в ферромагнетике относительно изменения напряженности внешнего магнитного поля, приводящее к неоднозначной зависимости В от Н, называют магнитным гистерезисом.
Вследствие гистерезиса при убывании Н до нуля образец полностью не размагничивается. Значение Вос называют остаточной индукцией.
Чтобы полностью размагнитить образец, изменяют направление внешнего магнитного поля на противоположное. Тогда при определенной напряженности (точка - Нк) индукция В становится равной нулю.
Значение напряженности Нк внешнего магнитного поля, которое необходимо приложить к образцу для полного его размагничивания, называют коэрцитивной силой.
При дальнейшем увеличении Н образец вновь начинает намагничиваться (в противоположном направлении) до насыщения (точка С2).
При уменьшении внешнего магнитного поля до нуля опять обнаруживается существование в образце остаточной индукции (точка - Вос), а при последующем изменении направления внешнего поля на противоположное и увеличении его напряженности можно вновь полностью размагнитить образец (точка Нк).
При дальнейшем увеличении напряженности внешнего магнитного поля вновь наступает насыщение образца (точка С1) и кривая замыкается.
Изображенный на рисунке график называют статической петлей гистерезиса.
Установлено, что площадь петли гистерезиса численно равна работе, которую надо совершить для перемагничивания данного образца.
Форма петли гистерезиса представляет собой одну из основных магнитных характеристик любого ферромагнитного вещества.
ПРИМЕНЕНИЯ ФЕРРОМАГНЕТИЗМА
Ферромагнетики делятся на две большие группы. К первой относятся магнитомягкие материалы, у которых площадь петли гистерезиса мала (следовательно, малы Вос и Нк). К таким ферромагнетикам относят химически чистое железо, электротехническая сталь, пермаллой (сплав железа и никеля) и т.д. Эти вещества почти полностью теряют намагниченность после удаления их из внешнего магнитного поля. Магнитомягкие материалы используют в трансформаторах, генераторах переменного тока, электродвигателях.
У магнитожестких материалов площадь петли гистерезиса велика (следовательно, велики Вос и Нк). Эти материалы в значительной степени сохраняют свою намагниченность и после вынесения их за пределы внешнего магнитного поля.
К таким ферромагнетикам относятся углеродистая и хромистая сталь, а также некоторые сплавы. Магнитожесткие материалы используют для изготовления постоянных магнитов.
Большое применение в радиотехнике имеют ферриты – вещества, являющиеся химическими соединениями оксида железа с оксидами других металлов. Ферриты обладают одновременно свойствами и ферромагнетиков, и полупроводников. Их используют для изготовления сердечников катушек индуктивности, внутренних антенн малогабаритных приемников и т.д.
ПРИРОДА ФЕРРОМАГНЕТИЗМА
В отличие от диа- и парамагнетиков, у которых магнитные свойства определяются орбитальными магнитными моментами атомных электронов, магнитные свойства ферромагнетиков обусловлены спиновыми магнитными моментами электронов. Ферромагнитные вещества (всегда имеющие кристаллическую структуру) состоят из атомов, в которых не у всех электронов спиновые магнитные моменты взаимно скомпенсированы.
В ферромагнетиках существуют области самопроизвольного (спонтанного) намагничения, которые называют доменами. Размер доменов порядка 10 – 4 – 10 – 7 м. В каждом домене спиновые магнитные моменты атомных электронов имеют одинаковую ориентацию, вследствие чего домен оказывается намагниченным до состояния насыщения. Поскольку при отсутствии внешнего магнитного поля магнитные моменты доменов ориентированы хаотически, ферромагнитный образец в таких условиях в целом не намагничен.
Под действием
внешнего магнитного поля происходит ориентация магнитных моментов доменов по
направлению этого поля, поэтому результирующее магнитное поле в ферромагнетике
усиливается (В![]() В0).
В0).
Когда все магнитные моменты доменов под действием внешнего магнитного поля оказываются ориентированными по направлению этого поля, наступает насыщение ферромагнитного образца.
При температуре выше точки Кюри доменная структура разрушается и ферромагнетик теряет присущие ему свойства.
Ферромагнетики при намагничивании могут деформироваться. Это явление называется магнитострикцией.
14. Магнитный поток. Явление электромагнитной индукции. Закон электромагнитной индукции. Правило Ленца. Токи Фуко
|
α n S |
В случае однородного магнитного поля магнитный поток через поверхность находится по формуле: Ф = BS cosα, где В - модуль вектора магнитной индукции, S - площадь поверхности, α - угол между вектором магнитной индукции и нормалью к поверхности (нормаль - вектор, перпендикулярный поверхности). Магнитный поток в системе СИ измеряется в веберах. 1 Вб = 1Тл · м² 1Вб = 1 В · с |
В 1831 г. Фарадей экспериментально обнаружил, что во всяком замкнутом проводящем контуре при изменении магнитного потока через поверхность, ограниченную эти контуром, возникает электрический ток. Это явление называют электромагнитной индукцией, а возникающий ток - индукционным. Величина индукционного тока не зависит от способа, которым вызывается изменение магнитного потока, а определяется лишь скоростью изменения Ф.
Согласно правилу Ленца индукционный ток всегда направлен так, чтобы противодействовать причине, его вызывающей. Иными словами, индукционный ток всегда направлен так, что созданное им магнитное поле противодействует тому изменению магнитного потока, которое вызывает данный ток.
Для создания тока в цепи необходимо наличие э.д.с. Поэтому явление электромагнитной индукции свидетельствует о том, что при изменении магнитного потока A в контуре возникает э.д.с. индукции ei. Согласно закону Фарадея-Максвелла э.д.с. индукции, возникающая в контуре, равна скорости изменения магнитного потока, взятой с противоположным знаком.
Мгновенное значение э.д.с. индукции находят по формуле: εi = - dФ∕dt = -Ф´
Среднее значение э.д.с. индукции εi = - ∆Ф⁄∆t
Знак "-" в формулах ставится согласно правилу Ленца.
В случае, когда контур состоит из N витков (т.е. представляет собой соленоид или тороид)
εi = - dΨ∕dt, где Ψ = NФ (Ψ – потокосцепление)
Э.д.с. индукции возникает и тогда, когда контур неподвижен, а магнитное поле изменяется, и в том случае, когда магнитное поле постоянно, а проводник движется с пересечением линий магнитной индукции. Природа э.д.с. индукции в каждом из этих случаев различна.
В первом случае возникновение э.д.с. индукции обусловлено тем, что изменяющееся магнитное поле, в котором находится неподвижный контур, вызывает появление в нем вихревого электрического поля. Это поле не связано с электрическими зарядами, а неразрывно связано с переменным магнитным полем. Силовые линии этого поля замкнуты. При перемещении заряда по замкнутой траектории в этом поле совершается работа, отличная от нуля.
В случае, когда проводник движется в неизменном магнитном поле с пересечением линий магнитной индукции, возникновение э.д.с. индукции обусловлено действием сил Лоренца, т.е. э.д.с. имеет магнитную природу.
Индукционные токи, возникающие в сплошных металлических телах, называют токами Фуко. Чтобы уменьшить их вредное влияние (нагревание сердечников трансформаторов, генераторов переменного тока, электродвигателей) эти сердечники собирают из отдельных изолированных друг от друга пластин. Тепловое действие токов Фуко используется в индукционных печах для выплавки металлов в вакууме, что позволяет получить материалы исключительно высокой чистоты. Вихревые токи, возникающие в проводах, по которым текут переменные токи, направлены так, что ослабляют ток внутри провода и усиливают вблизи поверхности. В результате быстропеременный ток оказывается распределенным по сечению провода неравномерно - он как бы вытесняется на поверхность проводника. Это явление называют скин-эффектом или поверхностным эффектом. Из-за скин-эффекта внутренняя часть проводников в высокочастотных цепях оказывается бесполезной, поэтому проводники для таких цепей изготавливают в виде трубок. Токи Фуко также применяют для успокоения (демпфирования) подвижных частей гальванометров, сейсмографов и других приборов.
15. Явление самоиндукции. Токи при замыкании и размыкании цепи. Энергия магнитного поля
Электрический ток i, текущий в любом контуре, создает потокосцепление (полный магнитный поток) Ψ. При изменении i будет меняться Ψ, и, следовательно, в контуре будет индуцироваться э.д.с. Это явление называют самоиндукцией.
В соответствии с законом Био-Савара-Лапласа напряженность магнитного поля пропорциональна силе тока, вызвавшего поле. Отсюда следует, что ток в контуре i и создаваемый им полный магнитный поток Ψ пропорциональны друг другу:
Ψ = Li.
Коэффициент пропорциональности L между силой тока и полным магнитным потоком Ψ называют индуктивностью контура. Наблюдения и расчет показывают, что индуктивность контура зависит от его формы, размеров, числа витков и магнитной проницаемости сердечника (если он помещен в контур).
При изменении силы тока в контуре возникает э.д.с. самоиндукции. В случае, когда индуктивность контура неизменна, э.д.с. самоиндукции можно вычислить по формуле:
εs = - L di/dt = - L і′
Индуктивность проводника численно равна э.д.с. самоиндукции, возникающей в данном проводнике при изменении в нём тока на единицу тока за единицу времени. Единицу силы тока устанавливают из этой же формулы:
1В 1С = 1 Ом ·с = 1 Гн (генри)
1А
Явление возникновения э.д.с. индукции в одном из контуров при изменении силы тока в другом называют взаимной индукцией.
По правилу Ленца дополнительные токи, возникающие в проводнике вследствие самоиндукции, всегда направлены так, чтобы препятствовать изменениям тока, текущего в цепи. Это приводит к тому, что установление тока при замыкании цепи и убывание тока при размыкании цепи происходит не мгновенно, а постепенно.
Экстраток размыкания тем больше, чем большее число витков имеет контур. Поэтому в цепях тех электродвигателей и электрогенераторов, где после размыкания цепи остаются замкнутые контуры, вместо рубильников ставят рычажные реостаты, при пользовании которыми исключается возможность возникновения больших экстратоков.
Э.д.с самоиндукции противодействует увеличению электрического поля в цепи, возникающего при её замыкании, т.е. при подключении к ней источника тока. Поэтому для создания в проводнике с индуктивностью L тока должна быть совершена работа против сил вихревого электрического тока, появляющегося в проводнике с током при изменении его магнитного поля. Эта работа совершается за счет энергии источника тока, создающего ток в данном проводнике. Из закона сохранения энергии следует, что при этом энергия источника тока превращается в энергию магнитного поля тока. Энергию магнитного поля проводника с током определяют по формуле:
Wм = LI² /2
16. Электрический ток в металлах. Элементарная классическая теория проводимости металлов
Для выяснения природы носителей тока в металлах был поставлен ряд опытов.
Опыт Рикке (1901 г.)
| Cu | Al | Cu |
Три цилиндра с тщательно отполированными торцами складывались в один составной проводник, по которому в течение года в одном направлении пропускался электрический ток. Вес цилиндров не изменился. Следовательно, перенос заряда в металлах осуществлялся не атомами, а другими частицами, входящими в состав металлов. Такими частицами могли быть открытые Томсоном электроны.
Опыты Мандельштама и Папалекси (1913 г.), Стюарта и Толмена (1916 г.)
На катушку намотана проволока, присоединенная к чувствительному гальванометру. Катушку приводили во вращение, а затем резко тормозили. В момент торможения гальванометр показывал кратковременный ток, направление которого свидетельствовало о том, что он создается движением отрицательно заряженных частиц. Стюарт и Толмен определили удельный заряд q/m частиц. Он практически совпал с удельным зарядом электрона. Тем самым было доказано, что электрический ток в металлах представляет собой упорядоченное движение электронов.
В начале ХХ века Друде и Лоренцем была создана классическая электронная теория проводимости металлов. Её основные положения заключаются в следующем.
Металлы имеют кристаллическую решетку, в узлах которой находятся положительные ионы, а между ними движутся свободные электроны (электроны проводимости). Электроны проводимости ведут себя подобно одноатомному идеальному газу. В промежутках между соударениями они движутся совершенно свободно, пробегая в среднем некоторый путь λ. Однако, в отличие от атомов газа, пробег которых определяется соударением атомов друг с другом, электроны сталкиваются преимущественно не между собой, а с ионами кристаллической решетки. Эти столкновения приводят к установлению теплового равновесия между электронным газом и кристаллической решеткой.
В отсутствии внешнего электрического поля электроны проводимости совершают хаотическое тепловое движение со средней квадратичной скоростью vкв., зависящей от температуры металла (vкв ~ √Т). Когда к металлу приложено внешнее электрическое поле, электроны проводимости начинают двигаться со средней скоростью vср., пропорциональной напряженности электрического поля Е, образуя электрический ток. Эта скорость пренебрежимо мала по сравнению со средней квадратичной скоростью, поэтому во всех расчетах, связанных со столкновениями электронов проводимости с решеткой, скоростью движения электронов считают среднюю квадратичную скорость vкв.
С точки зрения электронной теории сопротивление металлов обусловлено соударениями электронов проводимости с ионами кристаллической решетки. С ростом температуры сопротивление металлических проводников увеличивается, так как, чем выше температура, тем интенсивнее колебания кристаллической решетки и тем чаще электроны сталкиваются с ними. Экспериментально установлено, что зависимость сопротивления чистых металлов от температуры выражается формулой R = Ro (1 + αt). Коэффициент пропорциональности α называют температурным коэффициентом сопротивления (α > 0).
В 1911 г. голландский физик Камерлинг-Оннес обнаружил, что при температурах, близких к абсолютному нулю, сопротивление некоторых химически чистых металлов (например, цинка, алюминия, олова, ртути, свинца), а также ряда сплавов скачком падает до нуля. Это явление получило название сверхпроводимости. Это явление не может быть объяснено на основе классической электронной теории проводимости. Объяснение этому явлению дает только квантовая механика. Классическая электронная теория проводимости оказалась не в состоянии объяснить зависимость сопротивления металлов от температуры (т.к. согласно этой теории R~√Т, на практике R~Т.
17. Основы квантовой теории металлов
В классической электронной теории проводимости металлов электроны проводимости могут обладать любыми значениями энергии. Согласно квантовой теории энергия электронов в любом кристаллическом теле (в частности, в металле) так же, как и энергия электронов в атоме квантуется. Это означает, что она может принимать лишь дискретные (т.е. разделенные конечными промежутками) значения, называемые уровнями энергии. Дозволенные уровни энергии в кристалле группируются в зоны. Чтобы понять происхождение зон, рассмотрим воображаемый процесс объединения атомов в кристалл. Пусть первоначально имеется N изолированных одинаковых атомов какого-либо вещества. Каждый электрон любого атома обладает одним из разрешенных значений энергии, т.е. занимает один из дозволенных энергетических уровней. В основном, невозбужденном состоянии атома суммарная энергия электронов имеет минимальное возможное значение. Казалось бы, что все электроны должны находиться на самом низком уровне. Однако электроны подчиняются принципу запрета Паули, который гласит, что в любой квантовой системе (атоме, молекуле, кристалле и т. д.) на каждом энергетическом уровне может находиться не более двух электронов, причем спины электронов, занимающих одновременно один и тот же уровень, должны иметь противоположные направления. Следовательно, на самом низком уровне атома может разместиться только два электрона, остальные занимают попарно более высокие уровни.
Пока атомы изолированы друг от друга, они имеют полностью совпадающие схемы энергетических уровней. Заполнение уровней электронами осуществляется в каждом атоме независимо от заполнения аналогичных уровней в других атомах.
По мере сближения атомов между ними возникает всё усиливающееся взаимодействие, которое приводит к изменению положения уровней. Вместо одного одинакового для всех N атомов уровня возникает N очень близких, но не совпадающих уровней. Таким образом, каждый уровень изолированного атома расщепляется в кристалле на N густо расположенных уровней, образующих полосу или зону.
Электроны внешней оболочки атома заполняют ряд энергетических уровней, составляющих валентную зону. Валентные электроны участвуют в электрических и химических процессах. Более низкие энергетические уровни входят в состав других зон, заполненных электронами, но эти зоны не играют роли в явлении электропроводности.
В металлах и полупроводниках существует большое число электронов, находящихся на более высоких энергетических уровнях. Эти уровни составляют зону проводимости. Электроны этой зоны, называемые электронами проводимости, совершают беспорядочное движение внутри тела, переходя от одних атомов к другим. Именно электроны проводимости обеспечивают высокую электропроводность металлов.
У металлов зона проводимости непосредственно примыкает к валентной зоне. Поэтому при нормальной температуре в металлах большое число электронов имеет энергию, достаточную для перехода из валентной зоны в зону проводимости. Практически каждый атом металла отдает в зону проводимости, по крайней мере, один электрон. Таким образом, число электронов проводимости в металлах не меньше числа атомов.
18. Электрический ток в растворах и расплавах электролитов. Закон Фарадея для электролиза
Электролитами называют водные растворы солей, кислот и щелочей, а также расплавы солей.
Распад на ионы молекул растворяемого вещества под действием молекул растворителя называют электролитической диссоциацией.
Если в электролит поместить два электрода (катод и анод) с некоторой разностью потенциалов, то ионы начнут двигаться упорядоченно: положительные к катоду, а отрицательные к аноду.
Электрический ток в электролитах представляет собой направленное движение ионов.
Процесс выделения вещества на электродах или вблизи них при прохождении тока через электролиты называю электролизом.
Применения электролиза.
1. Гальваностегия (золочение, серебрение, никелирование изделий).
2. Гальванопластика (получение копий).
3. Получение чистых металлов (медь, алюминий), а также очистка металлов от примесей.
4. Электрическая полировка металлических изделий.
5. Получение водорода.
Согласно закону Фарадея для электролиза:
масса вещества, выделившегося при электролизе, прямо пропорциональна силе тока и времени его прохождения через электролит.
m = k I t = k q
k – электрохимический эквивалент вещества (зависит от атомной массы и валентности вещества),
q – заряд, прошедший через раствор электролита за время t.
19. Электрический ток в газах. Самостоятельный и несамостоятельный разряд
При отсутствии облучения и при невысоких температурах газы практически не проводят электрический ток, т.е. являются диэлектриками. Газ становится электропроводным в результате ионизации. Ионизация может быть вызвана нагреванием газа до высокой температуры или действием ультрафиолетового, рентгеновского, гамма-излучения. Ионизация газа состоит в том, что нейтральные молекулы или атомы газа теряют электроны и превращаются в положительные ионы. Большинство освободившихся электронов остаются свободными, но некоторые присоединяются к молекулам (или атомам) и образуют отрицательные ионы. Таким образом, в результате ионизации в газе появляются три типа носителей заряда: положительные, отрицательные ионы и электроны.
При создании в газе электрического поля положительные ионы движутся к катоду, а электроны и отрицательные ионы - к аноду, образуя электрический ток.
Электрический ток через газ называют газовым разрядом.
Если разряд протекает только при действии ионизатора, то разряд является несамостоятельным. Если разряд может протекать без действия внешнего ионизатора, то его называют самостоятельным.
ВИДЫ САМОСТОЯТЕЛЬНОГО РАЗРЯДА.
1. Тлеющий разряд представляет собой ток малой плотности, возникающий при низком давлении (от сотых долей до нескольких мм.рт.ст.) и напряжении на электродах порядка нескольких сотен вольт. Тлеющий разряд сопровождается свечением столба газа. Его используют в светящихся рубках рекламы (заполненных неоном, аргоном), а также в лампах дневного света для возбуждения люминофора, которым покрыта внутренняя поверхность трубки.
2. Коронный разряд представляет собой ток через газ при атмосферном давлении, возникающий под действием неоднородного электрического поля высокой напряженности. Коронный разряд сопровождается слабым свечением и небольшим шумом. Коронный разряд наблюдается вблизи заостренных частей проводников в том случае, когда напряженность электрического поля возле проводника превышает 3 · 106 В/м. Причиной разряда является ударная ионизация газа, происходящая в области, непосредственно граничащей с проводником. Особенно нежелательно возникновение этого разряда в высоковольтных ЛЭП, так как он приводит к потерям электрической энергии. Коронный разряд используют в электрических фильтрах для очистки продуктов сгорания топлива.
3. Дуговой разряд – это ток большой плотности через газ при невысоких напряжениях (десятки вольт). Дуговой разряд сопровождается сильным свечением газа и очень высокой температурой (несколько тысяч градусов). Дуговой разряд поддерживается термоэлектронной эмиссией, происходящей с поверхности разогретого катода, и термической ионизацией молекул газа. Дуговой разряд применяют для дуговой сварки металлов; в электрометаллургии (в дуговых печах для выплавки металлов); в химических производствах (например, для получения из воздуха оксида азота в целях производства азотной кислоты); в качестве сильного источника света (в прожекторах, в дуговых лампах) и т.д.
4. Искровой разряд представляет собой пробой газа при кратковременном лавинообразном увеличении числа ионов в нем, происходящем в результате ударной ионизации при высоких напряжениях. Искровой разряд сопровождается свечением и звуковым эффектом, а также излучением электромагнитных волн. При искровом разряде в газе возникают каналы сильно ионизированного газа – стриммеры, по которым происходит распространение искрового разряда. Газ в стриммерах сильно нагревается, что приводит к резкому увеличению его давления. Стремясь расшириться, газ создает звуковые волны, вызывающие звуковые эффекты. Мощной разновидностью искрового разряда является молния. В технике искровой разряд используют для поджигания рабочей смеси в цилиндрах карбюраторных двигателей внутреннего сгорания.
20. Электрический ток в вакууме. Термоэлектронная эмиссия Ламповый диод. Электронно-лучевая трубка
Свободные электроны в металлах находятся в непрерывном хаотическом движении, но, несмотря на это, при невысоких температурах не вылетают за пределы металла. Происходит это потому, что каждый свободный электрон притягивается к близлежащим положительным ионам кристаллической решетки. Чтобы вылететь из металла, электрон должен преодолеть силы притяжения положительных ионов, т.е. совершить работу против этих сил, а для этого он должен обладать достаточной кинетической энергией.
Энергию, которую должен затратить электрон для того, чтобы вылететь за пределы металла, называют работой выхода из данного металла.
При нагревании металла средняя кинетическая энергия свободных электронов увеличивается, возрастает число электронов, у которых она становится равной или большей работы выхода, а поэтому при достаточно высоких температурах (1100 – 1200К) из металла начинает вылетать достаточно большое количество электронов.
Испускание электронов нагретыми металлами называют термоэлектронной эмиссией. Это явление лежит в основе принципа действия большинства электровакуумных приборов (радиоламп, электронно-лучевых трубок).
Электрический ток в вакууме представляет собой направленное движение электронов.
ВАКУУМНЫЙ ДИОД
Вакуумный диод – это двухэлектродная электронная лампа. Внутри стеклянного или керамического баллона, в котором создан вакуум (10 – 6 - 10 –7 мм.рт.ст) расположены нить накала, анод и катод.
Нитью накала является проволочка, через которую пропускают электрический ток. Катод представляет собой металлическую трубку, охватывающую нить накала, не касаясь её. Поверхность катода покрывают иногда слоем оксидов щелочноземельных элементов (например, бария), чтобы уменьшить работу выхода электронов из металла. При нагревании катода с его поверхности эмитируют электроны. Такой катод называют катодом косвенного накала. Если катодом является сама нить накала, то его называют катодом прямого накала. Анод представляет собой пустотелый металлический цилиндр, внутри которого коаксиально расположены нить накала и катод.
Вакуумный диод обладает односторонней проводимостью. Его используют для выпрямления переменного тока.
ЭЛЕКТРОННО-ЛУЧЕВАЯ ТРУБКА
Этот прибор предназначен для преобразования в видимое изображение различных электрических сигналов. Электронно-лучевая трубка представляет собой баллон, из которого выкачан воздух. В узкой и длинной части баллона находится электронная пушка. Она служит для получения узкого пучка электронов (электронного луча) и состоит из нити накала, катода, управляющего электрода, первого и второго анода.
Электроны, вылетевшие из катода, формируются остальными электродами электронной пушки в электронный луч, который, выйдя из отверстия второго анода и, пройдя через две пары отклоняющих электродов (две пары взаимно перпендикулярных пластин), попадает на экран, покрытый люминофором.
Электронно-лучевые трубки с электростатическим отклонением луча используют обычно в электронных осциллографах. Электронно-лучевые трубки с магнитным отклонением луча используют в качестве кинескопов телевизоров.
21-22. Собственная и примесная проводимость полупроводников
По значению своего удельного сопротивления полупроводники занимают промежуточное положение между металлами и диэлектриками. Однако деление веществ на группы по их удельным сопротивлениям условно, так как под действием ряда факторов (нагревание, облучение, наличие примесей) удельное сопротивление многих веществ изменяется, причем у полупроводников весьма значительно. Если у металлов с ростом температуры сопротивление увеличивается, то у полупроводников уменьшается.
К полупроводникам относят 12 химических элементов в средней части периодической системы, многие оксиды и сульфиды металлов, некоторые органические вещества. Наибольшее применение в науке и технике имеют германий и кремний.
Различают полупроводники собственные (т.е. беспримесные) и примесные. Примесные делят на донорные и акцепторные.
Проводимость собственных полупроводников
Рассмотрим механизм на примере кремния. Кремний обладает атомной пространственной решеткой с ковалентным типом связи между атомами. При абсолютных температурах, близких к абсолютному нулю, все связи являются заполненными, т.е. свободных заряженных частиц в кристалле нет. При нагревании или облучении некоторые парноэлектронные связи разрываются, появляются свободные электроны и вакантные места, называемые дырками.
У собственных полупроводников число появившихся при разрыве связей электронов и дырок одинаково, т.е. проводимость собственных полупроводников в равной степени обеспечивается свободными электронами и дырками.
Проводимость примесных полупроводников
Если внедрить в полупроводник примесь с валентностью большей, чем у собственного полупроводника, то образуется донорный полупроводник.(Например, при внедрении в кристалл кремния пятивалентного мышьяка. Один из пяти валентных электронов мышьяка остается свободным). В донорном полупроводнике электроны являются основными, а дырки неосновными носителями заряда. Такие полупроводники называют полупроводниками n- типа, а проводимость электронной.
Если внедрять в полупроводник примесь с валентностью меньшей, чем у собственного полупроводника, то образуется акцепторный полупроводник. (Например, при внедрении в кристалл кремния трехвалентного индия. У каждого атома индия не хватает одного электрона для образования парноэлектронной связи с одним из соседних атомов кремния. Каждая из таких незаполненных связей является дыркой). В акцепторных полупроводниках дырки являются основными, а электроны неосновными носителями заряда. Такие полупроводники называются полупроводниками p- типа, а проводимость дырочной.
23. Свойства p-n- перехода. Полупроводниковые диоды. Транзисторы
Это свойство используют для создания полупроводниковых диодов, которые применяют для выпрямления переменного тока. В полупроводниковом диоде р-n- переход можно получить, вплавляя, например, каплю индия в кристалл германия. Германий служит катодом, а индий – анодом. В результате диффузии атомов индия внутрь монокристалла германия у поверхности германия образуется область с проводимостью р - типа. Та область, куда не проникают атомы индия, имеет проводимость n – типа. Возникает р-n- переход. Кристалл помещают в металлический корпус.
Достоинствами полупроводниковых диодов являются их прочность, малая масса, долговечность. Однако они могут работать в ограниченном интервале температур (от – 70оС до + 125оС).
В начале 50-х годов ХХ века в науке стали применять транзисторы. Они содержат в себе два р-n- перехода. Транзисторы предназначены, главным образом, для усиления, генерирования и преобразования электрических колебаний различных частот. Наиболее массовый транзистор представляет собой пластинку германия, кремния или другого полупроводника, обладающего электронной или дырочной проводимостью, в объеме которой искусственно созданы две области, противоположные по электрической проводимости. Пластинка полупроводника и две области в ней образуют два р-n- перехода, каждый из которых обладает такими же электрическими свойствами, как и полупроводниковый диод. Независимо от структуры транзистора пластинку полупроводника называю базой Б, область меньшего объема – эмиттером Э, а область большего объема – коллектором К.
24. Свободные электромагнитные колебания в контуре. Формула Томсона
Электрическую цепь, состоящую из последовательно соединенных катушки индуктивности L и конденсатора емкостью С, называют колебательным контуром.
Если зарядить от источника тока конденсатор, а затем предоставить ему возможность разряжаться через катушку индуктивности, то в контуре возникает ток, который периодически изменяется как по величине, так и по направлению. Следовательно, периодически изменяются по модулю и направлению напряженность электрического поля в конденсаторе и индукция магнитного поля в катушке. Одновременные периодические изменения взаимосвязанных электрического и магнитного полей называют электромагнитными колебаниями.
Электромагнитные колебания, происходящие в колебательном контуре за счет расходования сообщенной этому контуру энергии, которая в дальнейшем не пополняется, называют свободными электромагнитными колебаниями.
Свободные колебания являются затухающими, так как контур обладает активным сопротивлением (проводящие части контура нагреваются). Часть энергии тока расходуется на излучение электромагнитных волн в пространство.
Рассмотрим свободные электромагнитные колебания в идеальном контуре без активного сопротивления (контуре Томсона). В таком контуре полная энергия W остается постоянной.
q² ⁄ 2С + Li² / 2 = const
Найдем производную по времени от полученного выражения:
(q² ⁄ 2С)' + (Li² / 2)' = (const)'
Согласно правилам дифференцирования, получим:
2qq' / 2C + 2Lii' / 2 = 0.
Отсюда следует, что ii' = - 1/LC · qq'.
Сила тока равна первой производной от заряда по времени (i = q'). Следовательно, первая производная от силы тока по времени i' является второй производной от заряда по времени (i' = q''). С учетом сказанного уравнение можно записать в виде:
q' q'' = - 1/LC · qq', т.е. q'' = - 1/LC · q.
Так как L > 0 и C > 0, то и 1/LC > 0. Поэтому можно считать, что 1/LC = ωo², т.е.
ωo = 1/√LC. Уравнение свободных электромагнитных колебаний в идеальном контуре будет иметь вид: q'' = - ωo² · q. Решением данного уравнения является q=qm ·cos ωot.
Собственную циклическую частоту ωo свободных электромагнитных колебаний в колебательном контуре определяют по формуле ωo = 1/√LC. Поскольку период колебаний Т связан с циклической частотой формулой Т = 2π/ ωo, это значит, что период свободных электромагнитных колебаний в контуре без активного сопротивления (R=0), т.е. без затухания, определяют по формуле Т = 2π √LC, которую называют формулой Томсона.
В реальных колебательных контурах, обладающих активным сопротивлением, свободные электромагнитные колебания являются затухающими.
25. Вынужденные электромагнитные колебания. Переменный ток
Электромагнитные колебания, происходящие в колебательном контуре под действием периодически изменяющейся э.д.с. источника переменного тока, подключенного к этому контуру, называют вынужденными.
Переменным называют ток, периодически изменяющийся по величине и по направлению. Иными словами, переменный ток это вынужденные электромагнитные колебания.
Переменный ток можно получить, используя проводящую рамку, вращающуюся в магнитном поле.
Пусть рамка вращается с постоянной угловой скоростью ω в однородном магнитном поле с индукцией В. Магнитный поток, пронизывающий рамку, Ф = ВS cosα. Угол α изменяется по закону α = ωt. Следовательно, Ф = ВS cos ωt.
Согласно закону электромагнитной индукции, ε = - N Ф', где N - число витков в рамке. Следовательно,
ε = - NBS(cos ωt)' = NBSω sinωt.
Обозначим NBSω = εm (εm - амплитудное значение э.д.с.)
Получаем для э.д.с., возникающей в рамке, выражение
ε = εm sinωt.
Следовательно, э.д.с. в рамке изменяется по гармоническому закону. Разделив обе части равенства на R, получим
i = Im sinωt,
где i - мгновенное значение силы переменного тока, Im - амплитудное значение силы тока.
Действующие значения силы переменного тока и напряжения находят по формулам:
![]() ;
; ![]() .
.
Сопротивлением участка цепи переменного тока называют величину, равную отношению действующего (или амплитудного) значения напряжения на концах этого участка к действующему (или амплитудному) значению силы тока в данном участке цепи.
Одна и та же катушка индуктивности или конденсатор в цепи постоянного тока обладают одним сопротивлением, а в цепи переменного тока - другим сопротивлением. Следовательно, кроме активного сопротивления R в цепи переменного тока существуют и другие виды сопротивления.
Индуктивное сопротивление определяется по формуле XL = ωL.
Емкостное
сопротивление рассчитывают по формуле XС = ![]()
Установлено, что полное сопротивление Z, оказываемое переменному току цепью, содержащей активное, индуктивное и емкостное сопротивления, можно определить по формуле
![]() .
.




 +q1 -q2
+q1 -q2
 q
q

 В
В