
Рефераты по рекламе
Рефераты по физике
Рефераты по философии
Рефераты по финансам
Рефераты по химии
Рефераты по хозяйственному праву
Рефераты по экологическому праву
Рефераты по экономико-математическому моделированию
Рефераты по экономической географии
Рефераты по экономической теории
Рефераты по этике
Рефераты по юриспруденции
Рефераты по языковедению
Рефераты по юридическим наукам
Рефераты по истории
Рефераты по компьютерным наукам
Рефераты по медицинским наукам
Рефераты по финансовым наукам
Рефераты по управленческим наукам
Психология педагогика
Промышленность производство
Биология и химия
Языкознание филология
Издательское дело и полиграфия
Рефераты по краеведению и этнографии
Рефераты по религии и мифологии
Рефераты по медицине
Реферат: Дефекты в кристаллах
Реферат: Дефекты в кристаллах
Дефекты в кристаллах
Всякий реальный кристалл не имеет совершенной структуры и обладает рядом нарушений идеальной пространственной решетки, которые называются дефектами в кристаллах.
Дефекты в кристаллах подразделяют на нульмерные, одномерные и двумерные. Нульмерные (точечные) дефекты можно подразделить на энергетические, электронные и атомные.
Наиболее распространены энергетические дефекты — фононы — временные искажения регулярности решетки кристалла, вызванные тепловым движением. К энергетическим дефектам кристаллов относятся также временные несовершенства решетки (возбужденные состояния), вызываемые воздействием различных радиаций: света, рентгеновского или γ-излучения, α-излучения, потока нейтронов.
К электронным дефектам относятся избыточные электроны, недостаток электронов (незаполненные валентные связи в кристалле — дырки) и экситоны. Последние представляют собой парные дефекты, состоящие из электрона и дырки, которые связаны кулоновскими силами.
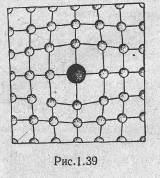
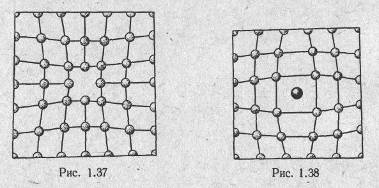
Атомные дефекты проявляются в виде вакантных узлов (дефекты Шотки, рис. 1.37), в виде смещения атома из узла в междоузлие (дефекты Френкеля, рис. 1.38), в виде внедрения в решетку чужеродного атома или иона (рис. 1.39). В ионных кристаллах для сохранения электронейтральности кристалла концентрации дефектов Шотки и Френкеля должны быть одинаковыми как для катионов, так и для анионов.
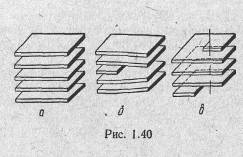
К линейным (одномерным) дефектам кристаллической решетки относятся дислокации (в переводе на русский язык слово «дислокация» означает «смещение»). Простейшими видами дислокаций являются краевая и винтовая дислокации. О характере их можно судить по рис. 1.40—1.42.
На рис. 1.40, а изображено строение идеального кристалла в виде семейства параллельных друг другу атомных плоскостей. Если одна из этих плоскостей обрывается внутри кристалла (рис. 1.40, б), то место обрыва ее образует краевую дислокацию. В случае винтовой дислокации (рис. 1.40, в) характер смещения атомных плоскостей иной. Здесь нет обрыва внутри кристалла какой-нибудь из атомных плоскостей, но сами атомные плоскости представляют собой систему, подобную винтовой лестнице. По существу, это одна атомная плоскость, закрученная по винтовой линии. Если обходить по этой плоскости вокруг оси винтовой дислокации (штриховая линия на рис. 1.40, в), то с каждым оборотом будем подниматься или опускаться на один шаг винта, равный межплоскостному расстоянию.
Детальное исследование строения кристаллов (с помощью электронного микроскопа и другими методами) показало, что монокристалл состоит из большого числа мелких блоков, слегка дезориентированных друг относительно друга. Пространственную решетку внутри каждого блока, можно считать достаточно совершенной, но размеры этих областей идеального порядка внутри кристалла очень малы: полагают, что линейные размеры блоков лежат в пределах от 10-6 до 10 -4см.
Любая конкретная дислокация может быть представлена как сочетание краевой и винтовой дислокации.
К двумерным (плоскостным) дефектам относятся границы между зернами кристаллов, ряды линейных дислокаций. Сама поверхность кристалла тоже может рассматриваться как двумерный дефект.
Точечные дефекты типа вакансий имеются в каждом кристалле, как бы тщательно он ни выращивался. Более того, в реальном кристалле вакансии постоянно зарождаются и исчезают под действием тепловых флуктуации. По формуле Больцмана равновесная концентрация вакансий пв в кристалле при данной температуре (Т) определится так:
![]() (1.1)
(1.1)
где п — число атомов в единице объема кристалла, е — основание натуральных логарифмов, k — постоянная Больцмана, Ев — энергия образования вакансий.
Для большинства кристаллов энергия образования вакансий примерно равна 1 эв, при комнатной температуре kT » 0,025 эв,
следовательно,
![]()
При повышении температуры относительная концентрация вакансий довольно быстро растет: при Т = 600° К она достигает 10-5, а при 900° К—10-2.
Аналогичные рассуждения можно сделать относительно концентрации дефектов по Френкелю, с учетом того, что энергия образования внедрений значительно больше (порядка 3—5 эв).
Хотя относительная концентрация атомных дефектов может быть небольшой, но изменения физических свойств кристалла, вызванные ими, могут быть огромными. Атомные дефекты могут влиять на механические, электрические, магнитные и оптические свойства кристаллов. В качестве иллюстрации приведем лишь один пример: тысячные доли атомного процента некоторых примесей к чистым полупроводниковым кристаллам изменяют их электрическое сопротивление в 105—106 раз.
Дислокации, являясь протяженными дефектами кристалла, охватывают своим упругим полем искаженной решетки гораздо большее число узлов, чем атомные дефекты. Ширина ядра дислокации составляет всего несколько периодов решетки, а длина его достигает многих тысяч периодов. Энергия дислокаций оценивается величиной порядка 4 • 10 -19 дж на 1 м длины дислокации. Энергия дислокаций, рассчитанная на одно межатомное расстояние вдоль длины дислокации, для разных кристаллов лежит в пределах от 3 до 30эв. Такая большая энергия, необходимая для создания дислокаций, является причиной того, что число их практически не зависит от температуры (атермичность дислокаций). В отличие от вакансий [см. формулу (1.1), вероятность возникновения дислокаций за счет флуктуации теплового движения исчезающе мала для всего интервала температур, в котором возможно кристаллическое состояние.
Важнейшим свойством дислокаций является их легкая подвижность и активное взаимодействие между собой и с любыми другими дефектами решетки. Не рассматривая механизм движения дислокаций, укажем, что для того, чтобы вызвать движение дислокации, достаточно создать в кристалле небольшое напряжение сдвига порядка 0,1кГ/мм2. Уже под влиянием такого напряжения дислокация будет перемещаться в кристалле, пока не встретит какого-либо препятствия, которым может быть граница зерна, другая дислокация, атом внедрения и т. д. При встрече с препятствием дислокация искривляется, огибает препятствие, образуя расширяющуюся дислокационную петлю, которая затем отшнуровывается и образует отдельную дислокационную петлю, причем в области обособленной расширяющейся петли остается отрезок линейной дислокации (между двумя препятствиями), который под воздействием достаточного внешнего напряжения снова будет изгибаться, и весь процесс повторится снова. Таким образом, видно, что при взаимодействии движущихся дислокаций с препятствиями происходит рост числа дислокаций (их размножение).
В недеформированных металлических кристаллах через площадку в 1 см2 проходит 106—108 дислокаций, при пластической деформации плотность дислокаций возрастает в тысячи, а иногда и в миллионы раз.
Рассмотрим, какое влияние оказывают дефекты кристалла на его прочность.
Прочность идеального кристалла можно рассчитать как силу, необходимую для того, чтобы оторвать атомы (ионы, молекулы) друг от друга, либо сдвинуть их, преодолев силы межатомного сцепления, т. е. идеальная прочность кристалла должна определяться произведением величины сил межатомной связи на количество атомов, приходящихся на единицу площади соответствующего сечения кристалла. Прочность же реальных кристаллов на сдвиг обычно на три-четыре порядка ниже расчетной идеальной прочности. Такое большое снижение прочности кристалла нельзя объяснить уменьшением рабочей площади поперечного сечения образца за счет пор, каверн и микротрещин, так как при ослаблении прочности в 1000 раз каверны должны были бы занимать 99,9% площади поперечного сечения кристалла.
С другой стороны, прочность монокристаллических образцов, во всем объеме которых сохраняется приблизительно единая ориентация кристаллографических осей, значительно ниже прочности поликристаллического материала. Известно также, что в ряде случаев кристаллы с большим числом дефектов обладают более высокой прочностью, чем кристаллы с меньшим количеством дефектов. Сталь, например, представляющая собой железо, «испорченное» примесью углерода и другими присадками, обладает значительно более высокими механическими свойствами, чем чистое железо.
Несовершенство кристаллов
До сих пор мы рассматривали идеальные кристаллы. Это позволило нам объяснить ряд характеристик кристаллов. На самом деле кристаллы не являются идеальными. В них могут в большом количестве присутствовать разнообразные дефекты. Некоторые свойства кристаллов, в частности электрические и другие, также зависят от степени совершенства этих кристаллов. Такие свойства называют структурно – чувствительными свойствами. Существуют 4 основных типа несовершенств в кристалле и ряд не основных.
К основным несовершенствам относится:
1) Точечные дефекты. Они включают в себя пустые узлы в решетке (вакансии), междоузельные лишние атомы, примесные дефекты (примеси замещения и примесь внедрения).
2) Линейные дефекты. (дислокации).
3) Плоскостные дефекты. Они включают в себя: поверхности всевозможные других включений, трещины, наружная поверхность.
4) Объемные дефекты. Включают в себя сами включения, чужеродные примеси.
К не основным несовершенствам относится:
1) Электроны и дырки – электронные дефекты.
2) Фононы, фотоны и другие квазичастицы, которые существуют в кристалле ограниченное время
Фактически они не оказывали влияние на энергетический спектр кристалла в невозбужденном состоянии. Однако, в реальных условиях, при T¹0 (абсолютная температура), электроны и дырки могут быть возбужденные в самой решетке, с одной стороны, а с другой стороны могут инжектироваться (вводится) в нее из вне. Такие электроны и дырки могут приводить с одной стороны к деформации самой решетки, а с другой стороны, за счет взаимодействия с другими дефектами, нарушать энергетический спектр кристалла.
Их нельзя рассматривать как истинное несовершенство. Хотя фотоны и обладают определенной энергией и импульсом, но если эта энергии не достаточно для генерации электронно – дырочных пар, то в этом случае кристалл будет прозрачен для фотона, то есть он без взаимодействия с материалом будет свободно проходить через него. Его включают в классификацию потому, что они могут оказывать влияние на энергетический спектр кристалла за счет взаимодействия с другими несовершенствами, в частности с электронами и дырками.
Точечные несовершенства (дефект)
При T¹0 может оказаться, что энергия частиц в узлах кристаллической решетки окажется достаточной для перевода частицы из узла в междоузлие. При чем каждой определенной температуре будет соответствовать свой определенная концентрация таких точечных дефектов. Часть дефектов будет образовываться за счет перевода частиц из узлов в междоузлие, а часть из них будет рекомбинировать (уменьшение концентрации) за счет перехода из междоузлий в узлы. За счет равенства потоков для каждой температуры будет соответствовать своя концентрация точечных дефектов. Такой дефект, который представляет собой совокупность междоузельного атома и оставшегося свободного узла), кансии) есть дефект по Френкелю. Частица из приповерхностного слоя, за счет температуры, может выйти на поверхность), поверхность является бесконечным стоком этих частиц). Тогда в приповерхностном слое образуется один свободный узел (вакансия). Этот свободный узел может быть занят более глубоко лежащим атомом, что эквивалентно перемещению вакансий в глубь кристалла. Такие дефекты называют дефектами по Шотки. Можно представить себе следующий механизм образования дефектов. Частица с поверхности перемещается в глубь кристалла и в толще кристалла появляется лишние междоузельные атомы без вакансий. Такие дефекты называют антишоткиевские дефекты.
Образование точечных дефектов
Существует три основных механизма образования точечных дефектов в кристалле.
Закалка. Кристалл нагревают до значительной температуры (повышенной), при этом каждой температуре соответствует вполне определенная концентрация точечных дефектов (равновесная концентрация). При каждой температуре устанавливается равновесная концентрация точечных дефектов. Чем больше температура, тем больше концентрация точечных дефектов. Если таким образом нагретый материал резко охладить, то в этом случае эта избыточная точечных дефектов окажется замороженной, не соответствующей этой низкой температуре. Таким образом, получают избыточную, по отношению к равновесной концентрации точечных дефектов.
Воздействие на кристалл внешними силами (полями). В этом случае к кристаллу подводится энергия, достаточная для образования точечных дефектов.
Облучение кристалла частицами высоких энергий. За счет внешнего облучения в кристалле возможны три основных эффекта:
1) Упругое взаимодействие частиц с решеткой.
2) Не упругое взаимодействие (ионизация электронов в решетке) частиц с решеткой.
3) Все возможные ядерные транс мутации (превращения).
Во 2-м и 3-м эффектах всегда присутствует и первый эффект. Эти упругие взаимодействия сказываются двояко: с одной стороны проявляются в виде упругих колебаний решетки, к образованию структурных дефектов, с другой стороны. При этом энергия падающего излучения должна превосходить пороговую энергию образования структурных дефектов. Эта пороговая энергия обычно в 2 –3 раза превосходит энергию, необходимую для образования такого структурного дефекта в адиабатических условиях. В адиабатических условиях для кремния (Si) энергия адиабатического образования составляет 10 эВ, пороговая энергия = 25 эВ. Для образования вакансии в кремнии, необходимо чтобы энергия внешнего излучения как минимум была больше 25 Эв, а не 10 эВ как для адиабатного процесса. Возможен вариант, что при значительных энергиях падающего излучения одна частица (1 квант) приводит к образованию не одного, а нескольких дефектов. Процесс может носить каскадный характер.
Концентрация точечных дефектов
Найдем концентрацию дефектов по Френкелю.
Предположим, что в узлах
кристаллической решетки расположено N частиц. Из них n частиц перешли из узлов
в междоузлие. Пусть энергия образования дефектов по Френелю будет Eф. Тогда
вероятность того, что еще одна частица перейдет из узла в междоузлие будет
пропорциональна числу сидящих еще в узлах частиц (N-n), и больцмановскому
множителю ![]() ,
то есть ~
,
то есть ~![]() . А общее число частиц перешедших
из узлов в междоузлие ~
. А общее число частиц перешедших
из узлов в междоузлие ~![]() . Найдем число
частиц переходящих из междоузлий в узлы (рекомбинирует). Это число
пропорционально n, и пропорционально числу свободных мест в узлах, а точнее
вероятности того, что частица наткнется на пустой узел, (то есть ~
. Найдем число
частиц переходящих из междоузлий в узлы (рекомбинирует). Это число
пропорционально n, и пропорционально числу свободных мест в узлах, а точнее
вероятности того, что частица наткнется на пустой узел, (то есть ~![]() ). ~
). ~![]() . Тогда суммарное изменение числа
частиц будет равна разности этих величин:
. Тогда суммарное изменение числа
частиц будет равна разности этих величин:
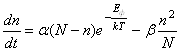 .
.
С течением времени потоки
частиц из узлов в междоузлия и в обратном направлении станут, равны друг другу
то есть, устанавливается стационарное состояние. Так как число частиц в
междоузлиях много меньше общего числа узлов, то n можно пренебречь и ![]() . Отсюда найдем
. Отсюда найдем
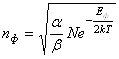
– концентрация дефектов
по Френкелю, где a и b – неизвестные коэффициенты.
Используя статистический подход, к концентрации дефектов по Френкелю и учтя,
что N’ – число междоузлий, мы можем найти концентрацию дефектов по Френкелю: ![]() , где N –
число частиц, N’ – число междоузлий.
, где N –
число частиц, N’ – число междоузлий.
Процесс образования дефектов по Френкелю является бимолекулярным процессом (2-х частичный процесс). В то же время процесс образования дефектов по Шотки, является мономолекулярным процессом.
Дефект по Шотки
представляет одну вакансию. Проведя аналогичные рассуждения, как и для
концентрации дефектов по Френкелю, получим концентрацию дефектов по Шотки в
следующем виде: ![]() , где nш – концентрация дефектов
по Шотки, Eш – энергия образования дефектов по Шотки. Так как процесс
образования по Шотки является мономолекулярным, то в отличие от дефектов по
Френкелю, в знаменателе показателя экспоненты отсутствует 2. Процесс
образования, например дефектов по Френкелю, характерно для атомных кристаллов.
Для ионных кристаллов дефекты, например по Шотки, могут образовываться лишь
парами. Это происходит потому, что для сохранения электронейтральности ионного
кристалла необходимо, чтобы на поверхность выходили одновременно пары ионов
противоположного знака. То есть концентрация таких парных дефектов может быть
представлена в виде бимолекулярного процесса:
, где nш – концентрация дефектов
по Шотки, Eш – энергия образования дефектов по Шотки. Так как процесс
образования по Шотки является мономолекулярным, то в отличие от дефектов по
Френкелю, в знаменателе показателя экспоненты отсутствует 2. Процесс
образования, например дефектов по Френкелю, характерно для атомных кристаллов.
Для ионных кристаллов дефекты, например по Шотки, могут образовываться лишь
парами. Это происходит потому, что для сохранения электронейтральности ионного
кристалла необходимо, чтобы на поверхность выходили одновременно пары ионов
противоположного знака. То есть концентрация таких парных дефектов может быть
представлена в виде бимолекулярного процесса: ![]() . Теперь можно найти отношение
концентраций дефектов по Френкелю к концентрации дефектов по Шотки:
. Теперь можно найти отношение
концентраций дефектов по Френкелю к концентрации дефектов по Шотки: ![]() ~
~![]() . Энергия образования парных
дефектов по Шотки Eр и энергия образования дефектов по Френкелю Eф имеют
величину порядка 1 эВ и могут отличаться друг от друга порядка нескольких
десятых эВ. KT для комнатных температур имеет значение порядка 0,03 эВ. Тогда
. Энергия образования парных
дефектов по Шотки Eр и энергия образования дефектов по Френкелю Eф имеют
величину порядка 1 эВ и могут отличаться друг от друга порядка нескольких
десятых эВ. KT для комнатных температур имеет значение порядка 0,03 эВ. Тогда ![]() ~
~![]() . Отсюда следует, что для
конкретного кристалла будет преобладать один конкретный тип точечных дефектов.
. Отсюда следует, что для
конкретного кристалла будет преобладать один конкретный тип точечных дефектов.
Скорость перемещения дефектов по кристаллу
Диффузия – есть процесс перемещения частиц в кристаллической решетке на макроскопические расстояния вследствие флуктуации (изменения) тепловой энергии. Если перемещающиеся частицы являются частицы самой решетки, то речь идет о самодиффузии. Если в перемещении участвуют частицы, являющиеся чужеродными, то речь идет о гетеродиффузии. Перемещение этих частиц в решетке может осуществлятся несколькими механизмами:
- За счет движения междоузельных атомов.
- За счет движения вакансий.
- За счет взаимного обмена мест междоузельных атомов и вакансий.
Диффузия за счет движения междоузельных атомов
Фактически носит двухступенчатый характер:
- Междоузельный атом должен образоваться в решетке.
- Междоузельный атом должен перемещаться в решетке.
 |
Положением в междоузлиях соответствует минимум потенциальной энергии
Пример: имеем пространственную решетку. Частица в междоузлии.
Для того, чтобы частица
перешла из одного междоузлия в соседнее, она должна преодолеть потенциальный
барьер высотой Em. Частота перескоков частиц из одного междоузлия в другое
будет пропорциональна ![]() . Пусть частота колебания частиц,
соответствует междоузлию v. Число соседних междоузлий равно Z. Тогда частота
перескоков:
. Пусть частота колебания частиц,
соответствует междоузлию v. Число соседних междоузлий равно Z. Тогда частота
перескоков: ![]() .
.
Диффузия за счет движений вакансий
Процесс диффузии за счет
вакансий также является 2-х ступенчатым. С одной стороны, вакансии должны
образовываться, с другой стороны, она должна перемещаться. Следует отметить,
что свободное место (свободный узел), куда может переместиться частица,
существует также лишь определенную долю времени пропорционально ![]() , где Ev – энергия
образования вакансий. А частота перескоков будет иметь вид:
, где Ev – энергия
образования вакансий. А частота перескоков будет иметь вид: ![]() , где Em – энергия
движения вакансий, Q=Ev+Em – энергия активации диффузии.
, где Em – энергия
движения вакансий, Q=Ev+Em – энергия активации диффузии.
Перемещение частиц на большие расстояния
Рассмотрим цепочку одинаковых атомов.
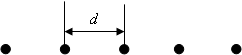 Предположим, что
имеем цепочку одинаковых атомов. Они расположены на расстоянии d друг от друга.
Частицы могут смещаться влево или в право. Среднее смещение частиц равно 0. В
силу равновероятности перемещения частиц в обоих направлениях:
Предположим, что
имеем цепочку одинаковых атомов. Они расположены на расстоянии d друг от друга.
Частицы могут смещаться влево или в право. Среднее смещение частиц равно 0. В
силу равновероятности перемещения частиц в обоих направлениях:
![]() .
.
Найдем среднеквадратичное смещение:
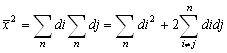 .
. 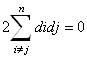 .
. ![]() ,
,
где n – число переходов
частиц, может быть выражено ![]() . Тогда
. Тогда ![]() . Величина
. Величина ![]() определяется
параметрами данного материала. Поэтому обозначим:
определяется
параметрами данного материала. Поэтому обозначим: ![]() – коэффициент диффузии, в итоге:
– коэффициент диффузии, в итоге:
![]() .
.
В 3-х мерном случае:
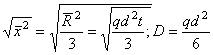 .
.
Подставим сюда значение q, получим:
![]() .
.
Где D0 – частотный фактор диффузии, Q – энергия активации диффузии.
Макроскопическая диффузия

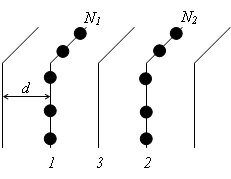 |
Рассмотрим простую кубическую решетку:
Мысленно между
плоскостями 1 и 2 условно выделим плоскость 3. и найдем число частиц,
пересекающих эту полуплоскость слева на право и справа на лево. Пусть частота
перескоков частиц равна q. Тогда за время, равное ![]() , полуплоскость 3 пересечет со
стороны полуплоскости 1
, полуплоскость 3 пересечет со
стороны полуплоскости 1 ![]() частиц. Аналогично, за это же
время
частиц. Аналогично, за это же
время ![]() выделенную
полуплоскость со стороны полуплоскости 2 пересечет
выделенную
полуплоскость со стороны полуплоскости 2 пересечет ![]() частиц. Тогда за время t
изменение числа частиц в выделенной полуплоскости можно представить в следующем
виде:
частиц. Тогда за время t
изменение числа частиц в выделенной полуплоскости можно представить в следующем
виде: ![]() .
Найдем концентрацию частиц – примесей в полуплоскостях 1 и 2:
.
Найдем концентрацию частиц – примесей в полуплоскостях 1 и 2:
 .
.
Разность объемных концентраций C1 и C2 можно выразить в виде:
![]() .
.
![]() .
.
Рассмотрим единичный
выделенный слой (L2=1). Мы знаем, что ![]() – коэффициент диффузии, тогда:
– коэффициент диффузии, тогда:
![]() – 1-й закон диффузии Фика.
– 1-й закон диффузии Фика.
Аналогично формула для
3-х мерного случая. Только в место одномерного коэффициента диффузии ![]() , подставляем
коэффициент диффузии для 3-х мерного случая
, подставляем
коэффициент диффузии для 3-х мерного случая ![]() . Используя такую аналогию
рассуждения для концентрации, а не для числа носителей, как в предыдущем
случае, можно найти 2-й диффузии Фика.
. Используя такую аналогию
рассуждения для концентрации, а не для числа носителей, как в предыдущем
случае, можно найти 2-й диффузии Фика.
![]() – 2-й закон Фика.
– 2-й закон Фика.
2-й закон диффузии Фика очень удобен для расчетов, для практических приложений. В частности для коэффициента диффузии различных материалов. Например, имеем какой-то материал, на поверхность которого нанесена примесь, поверхностная концентрация которой равна Q см-2. Нагревая данный материал, осуществляют диффузию этой примеси в ее объем. В этом случае, в зависимости от времени устанавливается определенное распределение примеси, по толще материала для данной температуры. Аналитически распределение концентрации примеси, можно получить, решая уравнение диффузии Фика в следующем виде:
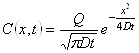 .
.
Графически это:
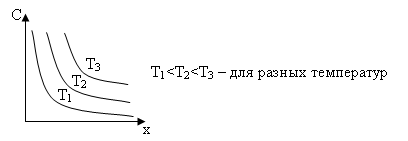
На этом принципе можно экспериментально найти параметры диффузии.
Экспериментальные методы исследования диффузии
Активационный метод
На поверхность материала наносят радиоактивную примесь, далее осуществляют диффузию этой примеси в материал. Затем послойно удаляют часть материала и исследуют активность, или оставшегося материала, или стравленного слоя. И таким образом находят распределение концентрации C по поверхности X(C(x)). Затем, используя полученное экспериментальное значение и последнею формулу, вычисляют коэффициент диффузии.
Они основаны на том, что при диффузии примеси, в результате ее взаимодействия с основным материалом образуется новые химические соединения с отличными от основных свойств решетки.
За счет диффузии примеси в полупроводниках на какой-то глубине полупроводника образуется область, в которой меняется тип его проводимости. Далее определяют глубину залегания p-n перехода и по ней судят о концентрации примесей на этой глубине. И далее делают по аналогии с 1-ым и 2-ым случаем.
Список использованных источников
1. Киттель Ч. Введение в физику твердого тела./ Пер. с англ.; Под ред. А. А. Гусева. – М.: Наука, 1978.
2. Епифанов Г.И. Физика твердого тела: Учеб. пособие для втузов. – М.: Высш. школ, 1977.
3. Жданов Г.С., Хунджуа Ф.Г., Лекции по физике твердого тела – М: Изд-во МГУ, 1988.
4. Бушманов Б. Н., Хромов Ю. А. Физика твердого тела: Учеб. пособие для втузов. – М.: Высш. школ, 1971.
5. Кацнельсон А.А. Введение в физику твердого тела – М: Изд-во МГУ, 1984.