Курсовая работа: Создание программы для определения вершин пирамиды с выпуклым основанием по данным точкам

КУРСОВОЙ ПРОЕКТ

по дисциплине

«Программирование на языке высокого уровня»

на тему:

«Создание программы для определения вершин пирамиды с выпуклым основанием по данным точкам»

Введение

Целью данного проекта – является закрепление материала, изложенного в курсе «Программирование на языке высокого уровня» на основе какой-либо обобщающей задачи. В качестве таковой была выбрана задача определения пирамиды с выпуклым основанием по данным N точкам.

Данная задача предполагает укрепление знаний в линейной алгебре и закрепление их в виде решения поставленной задачи на языке высокого уровня(Pascal)

Постановка Задачи

Разработать подпрограмму для определения вершин пирамиды с выпуклым основанием по данным точкам.

Создание демонстрационной программы для показа найденного решения. А так же создание библиотеки для работы с векторами в пространстве.

Теоретические сведения

Векторы

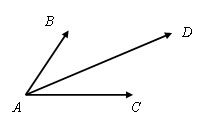
Вектором называется направленный отрезок.

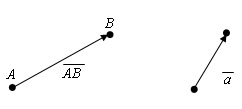
Описание: Вектор

У вектора есть начало и есть конец. Обозначается вектор строчными латинскими буквами a, b, c, ... или указанием его начала и конца, на первом месте всегда указывается начало. На чертежах вектор отмечается стрелкой. Иногда слово «вектор» не пишут, а ставят стрелочку над буквенным обозначением.

Вектор AB, AB, a

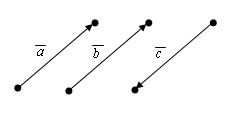
Описание: Вектор

Вектор AB и вектор CD называются одинаково направленными, если полупрямые AB и CD одинаково направлены

Вектор AB и вектор CD называются противоположно направленными, если полупрямые AB и CD противоположно направлены.

a и b одинаково направленные.

a и c противоположно направленные.

Абсолютной величиной вектора называется длина отрезка, изображающего вектор. Обозначается как |a| .

Вектором в пространстве называется направленный отрезок.

Координатами вектора с началом в точке A1(x1; y1; z1) и концом в точке A2(x2; y2; z2) называются числа x2-x1, y2-y1, z2-z1. Вектор обозначается в пространстве так:

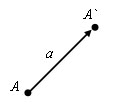
Описание: Координаты вектора

Есть вектора a. Пусть A (x; y) – начло вектора, а A` (x`; y`) – конец вектора. Координатами вектора a называются числа a1=x-x`, a2=y-y`. Для обозначения того, что вектор a имеет координаты a1 и a2, используют запись a (a1; a2) или (a1; a2).

Абсолютная величина вектора a (a1; a2) равна

Если начало вектора совпадает с его концом, то это нулевой вектор , обозначается (0).

Сложение векторов

Суммой векторов a(a1; a2) и b(b1; b2) называется вектор c(a1+b1; a2+b2).

Для любых векторов a(a1; a2), b(b1; b2), c(с1; с2) справедливы равенства:

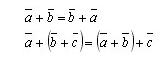
Описание: сложение векторов a+b=b+a, a+(b+c)=(a+b)+c

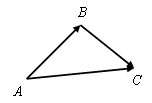
Описание: сложение векторов треугольник

Теорема Каковы бы ни были три точки A, B и C, имеет место векторное равенство

Доказательство.

Пусть A(x1; y1), B(x2; y2), C(x3; y3) – данные три точки.

Вектор AB имеет координаты (x2 – x1; y2 – y1), вектор BC имеет координаты (x3 – x2; y3 – y2). Следовательно, вектор AB + BCимеет координаты (x3 – x1;y3 – y1). А вектор AC имеет координаты (x3 – x1;y3 – y1). Значит, AC = AB+ BC. Теорема доказана.

Сложение векторов. Правило параллелограмма

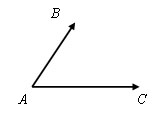
Описание: два вектора

Правилом параллелограмма сложения векторов называется следующий способ:

Пусть есть векторы AB и AC у которых начало вектора совпадает, а концы не совпадают

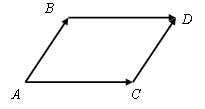
Описание: параллелограмм

Достроим данный угол до параллелограмма, так что AC = BD и AB = CD.

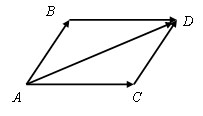
Описание: параллелограмм и диагональ

Тогда AB + BD = AD, а так как BD = AC, то AB + AC = AD

Описание: три вектора, сумма

Сложение векторов. Правило треугольника

Описание: сложение векторов правило треугольника

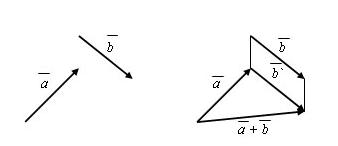
Правилом треугольника сложения векторов называется следующий способ:

Пусть есть произвольные векторы a и b. Надо от конца вектора a отложить вектор b`, равный вектору b. Тогда вектор, начало которого совпадает с началом вектора a, а конец совпадет с концом вектора b`, будет суммой a + b.

Свойство умножения вектора на число

Теорема

Абсолютная величина вектора λa равна |λ| |a|. Направление вектора λa при a≠ 0 совпадает с направлением вектора a, если λ>0, и противоположно направлению вектора a, если λ<0.

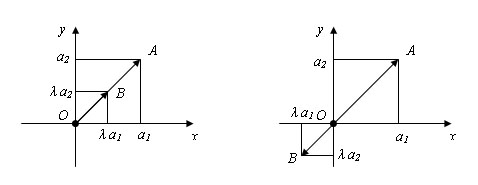
Описание: Свойство умножения вектора на число

Доказательство.

Построим векторы OA и OB равные a и λa соответственно (O – начало координат). Пусть a1 и a2 – координаты вектора a. Тогда координатами точки A будут числа a1 и a2 координатами точки B – числа λa1 и λa2. Уравнение прямой OA имеет вид: αx + βy = 0.

Так как уравнению удовлетворяют координаты точки A (a1; a2), то ему удовлетворяют и координаты точки B (λa1; λa2). Отсюда следует, что точка B лежит на прямой OA. Координаты c1 и c2 любой точки C, лежащей на луче OA, имеют те же знаки, что и координаты a1 и a2 точки A, и координаты любой точки, которая лежит на луче, дополнительном к OA, имеют противоположные знаки.

Поэтому, если λ > 0, то точка B лежит на луче OA, а следовательно, векторы a и λa одинаково направлены. Если λ < 0, то точка B лежит на дополнительном луче и векторы a и λa противоположно направлены.

Абсолютная величина вектора λa равна:

Теорема доказана.

Теорема

Равные векторы имеют равные соответствующие координаты.

Доказательство

Рассмотрим два случая: 1) векторы не лежат на одной прямой.

Описание: Координаты вектора. Векторы не на одной прямой

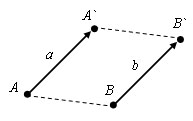
Пусть есть вектор a с началом в точке A (x; y) и концом в точке A` (x`; y`). При параллельном переносе получаем вектор b, у которого тогда начало будет в точке B(x+c; y+d), а конец в точке B`(x`+c; y`+d). Отсюда видно, что оба вектора будут иметь одни и тебе координаты (x-x`; y-y`).

2) векторы лежат на одной прямой.

Описание: Координаты вектора. Векторы на одной прямой

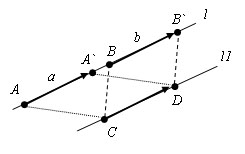
Пусть есть прямая l на которой лежат равные векторы AA` и BB`. A(x; y), A`(x`; y`), B(x1;y1) и B(x1`; y1`). Проведем прямую l1 параллельную l и отложим на ней вектор CD равный AA` и BB`, C (x0; y0) и D (x0`; y0`). Так как AA` = CD, из предыдущего пункта x-x`=x0-x0` и y-y`=y0-y0`. С другой стороны BB` = CD и x1-x1`=x0-x0`, y1-y1`=y0-y0`. Сравнивая равенства получаем x-x`=x1-x1` и y-y`=y1-y1`. Теорема доказана.

Произведение вектора a(a1; a2) на число λ называется вектор (λa1; λa2), т.е. (a1; a2) λ = (λa1; λa2).

Для любого вектора a и чисел λ, μ

Для любого вектора a и b и числа λ

Коллинеарный вектор

Описание: Коллинеарный вектор

Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Коллинеарные векторы либо одинаково направлены, либо противоположно направлены.

Коллинеарный вектор. Свойства

Теорема

Если есть два отличных от нуля коллинеарных вектора, то существует число λ такое, что

Доказательство.

Пусть a и b одинаково направлены.

- это векторы, которые одинаково направлены и имеют одну и ту же абсолютную величину |b|. Значит, они равны:

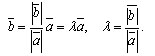
Описание: Коллинеарный вектор. Свойства формула3

Когда векторы a и b противоположно направлены аналогично заключаем, что

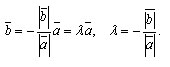
Описание: Коллинеарный вектор. Свойства формула4

Теорема доказана.

Теорема

Любой вектор с можно представить в виде

Скалярным произведением векторов a (a1; a2) и a (b1; b2) называется число a1b1+a2b2.

Для любых векторов a (a1; a2), b (b1; b2), c (с1; с2)

Углом между ненулевыми векторами AB и AC называется угол ABC. Углом между любыми двумя ненулевыми векторами a и b называется угол между равными им векторами с общим началом.

Скалярное произведение. Свойство

Теорема

Скалярное произведение векторов равно произведению их абсолютных величин на косинус угла между ними.

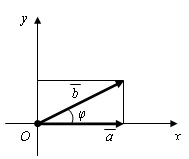
Описание: Скалярное произведение. Свойство

Доказательство.

Пусть a и b – данные векторы и φ – угол между ними. Имеем:

или

Скалярное произведение ab таким образом, выражается через длины векторов a, b и a + b т. е. систему координат можно выбрать любую, а величина скалярного произведения не изменится. Выберем систему координат xy так, чтобы начало координат совпало с началом вектора a, а сам вектор лежал на положительной полуоси оси Ox. Тогда координатами вектора a будут числа |a| и 0, а координатами вектора a – |a| cos φ и |a| sin φ . По определению

Теорема доказана.

Из теоремы следует, что если векторы перпендикулярны, то их скалярное произведение равно нулю.

Плоскость, многоугольники

Плоскость

Теорема

Через прямую и не лежащую на ней точку можно провести плоскость, и при том только одну.

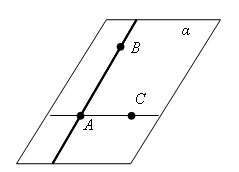
Описание: Плоскость и точка

Доказательство

Пусть AB – данная прямая и С – не лежащая на ней точка. Проведем через точки A и С прямую. Прямые AB и AC различны, так как точка С не лежит на прямой AB. Проведем через прямые AB и AC плоскость α. Она проходит через прямую AB и точку С.

Докажем, что плоскость α, проходящая через прямую AB и точку С, единственна.

Допустим, существует другая, плоскость α.`, проходящая через прямую AB и точку С. По аксиоме о том, что если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку, плоскости α и α` пересекаются по прямой. Эта прямая должна содержать точки A, B, C. Но они не лежат на одной прямой. Что противоречит предположению. Теорема доказана.

Выпуклый многоугольник

Описание: многоугольник

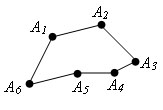
Ломаная называется замкнутой, если ее концы соединены отрезком.

Если все звенья простой замкнутой ломаной не лежат на одной прямой, то это многоугольник. Тогда точки ломанной называются вершинами многоугольника, а звенья – сторонами многоугольника.

Многоугольник с n вершинами, называется n-угольником.

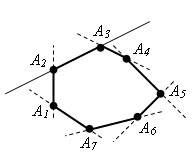
Описание: многоугольник выпуклый

Многоугольник называется выпуклым, если он лежит в одной полуплоскости относительно любой прямой, содержащей его сторону.A1A2A3A4A5A6A7 – выпуклый многоугольник.

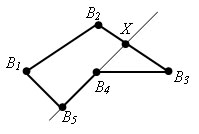
Описание: многоугольник невыпуклый

B1B2B3B4B5 – невыпуклый многоугольник.

Выпуклые многоугольники. Свойство

Теорема.

Сумма углов выпуклого n-угольника равна 180°*(n-2).

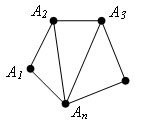
Описание: многоугольник выпуклый

Доказательство.

Нужно заметить, n ≥ 3.

Для n = 3 многоугольник превращается в треугольник и теорема справедлива.

Для n > 3 проведем n-3 диагонали: A2An, A3An, …, An-1An. Получим n-2 треугольника: Δ A1A2An, Δ A2A3An, …, An-2An-1An. Сумма углов всех треугольников равна сумме углов многоугольника. Так как сумма углов треугольнике равна 180 ° и число треугольников равно n – 2, то сумма всех углов многоугольника равна 180° * (n - 2). Теорема доказана.

ОПИСАНИЕ ОБЩЕГО АЛГОРИТМА

Пункт1.Пользователь вводит N точек.

Пункт2.Программа проверяет, лежат ли все данные точки в одной плоскости, если лежат-то решения нет, вершины пирамиды не будут найдены, а на дисплей выведется сообщение «точки лежат в одной плоскости».(переход к пункту 6)

Пункт3. Если все данные точки не лежат в одной плоскости, то программа берет N-1 точек (исключаемую точку принимая за возможную вершину пирамиды) и выполняет построение уравнения плоскости по 3-м точкам ,

Пункт4.Выполним проверку на принадлежность к данной плоскости оставшихся точек .В случае ,если хотя бы одна точка из оставшихся точек не принадлежит к плоскости, то переходим к пункту 6.

Пунтк5.Выполним проверку выпуклости многоугольника из полученной поверхности.( Проверка на выпуклость проверяется ,как условие сохранения знака векторного произведение смежных векторов). Если же проверка N-1 точек не даст того, что эти точки образуют плоскость, то из N точек будет взята другая точка и проведена еще проверка на выпуклость многоугольника. И так пока не будут перебраны все возможные точки.

В случае удачной проверки на выпуклость программа выдаст сообщение о том, что были определены вершины пирамиды с выпуклым основанием

Пункт6.вывод ответа

Описание структур данных

Для хранения точек был использован динамическая структура данных- односвязанный список. Элемент списка представляет собой запись с 2 полями:

-полем данных

-полем указателя на следующий элемент

В свою очередь поле данных представляет собой запись Coordinates с 3-я полями:x,y,z

Так же для работы со списком использовались дескрипторы ,которые представляли собой записи с 3-я полями

-start(указатель на начальный(фиктивный ) элемент)

-ptr(указатель на текущий элемент)

-Number(число элементов в записи)

Type

Coordinates=record {коориднаты}

x,y,z:real;

end;

P_Points=^point; {Описание типа Points}

point=record

data:Coordinates;

Next:P_Points;

end;

P_Descriptor=record {Дескриптор для работы со списком точек}

Start,Ptr:P_Points;

Number:Word;

end;

P_Vectors=^Vector; {Описание типа Vector}

Vector=record

data:Coordinates;

Next:P_Vectors;

end;

V_Descriptor=record {Дескриптор для работы со списком векторов}

V_Start,V_Ptr:P_Vectors;

V_Number:Word;

end;

Описание модуля

Спецификация подпрограмм для работы со списком

1.Спецификация процедуры InitListOfPoint;

1) Procedure InitListOfPoint(var P:P_Descriptor);;

2) Назначение: инициализирует фикивный элемент списка;

3) Входные параметры: P

4) Выходные параметры: P.

2.Спецификация процедуры PutPoint;

1) Procedure PutPoint(var P:P_Descriptor);

2) Назначение: создает элемент Buf и помещает его в список;

3) Входные параметры: P;

4) Выходные параметры: P;

3.Спецификация процедуры WritePoints;

1 Procedure WritePoints(var P:P_Descriptor);

2) Назначение: выводит весь список точек P на дисплей;

3) Входные параметры: P;

4) Выходные параметры: P.

4.Спецификация процедуры ReadPoint;

1) Procedure ReadPoint(var P:P_Descriptor;var a:Coordinates);

2) Назначение: cчитывает из списка P координаты точки в переменную а;

3) Входные параметры: P;

4) Выходные параметры: P,a.

5.Спецификация процедуры ClearMem;

1) Procedure ClearMem(var P:P_Descriptor;var V:V_Descriptor);

2) Назначение: освобождает выделенную память под списки P u V;

3) Входные параметры: P,V;

4) Выходные параметры: P,V.

Спецификация подпрограмм для работы с векторами

1.Спецификация процедуры CreateVector;

1) procedure CreateVector (a,b:Coordinates;var c:Coordinates);;

2) Назначение: создает вектор с вычитая соответствующие координаты точки b из точки a;

3)Входные параметры: a,b,c

4)Выходные параметры: c.

2.Спецификация процедуры MultOnNumber;

1) Procedure MultOnNumber (Number:real; a:Coordinates;var c:Coordinates)

2)Назначение: умножает вектор a на число real и полученное значение заносится в c вектор ;

3)Входные параметры: Number,a,c;

4)Выходные параметры: ,c;

3.Спецификация процедуры lengthOfVector;

1 Function lengthOfVector(a:Coordinates):real;

2Назначение: возвращает длину вектора а ;

3Входные параметры: а;

4Выходные параметры: -.

4.Спецификация процедуры Scalar;

1) Function Scalar(a,b:Coordinates):real;

2Назначение: возвращает результат скалярного перемножение векторов а и b ;

3Входные параметры: a,b;

4Выходные параметры: -.

5.Спецификация процедуры angle;

1) Function angle(a,b:coordinates):real

2Назначение: возвращает значение косинуса угла(в радианах)

между векторами а и b

3Входные параметры: a,b;

4Выходные параметры: -.

6.Спецификация процедуры VECTMult;

1 Procedure VECTMult(a,b:Coordinates;var c:Coordinates);

2Назначение: производит векторное перемножение вектора а и b и заносит результат в вектор с ;

3Входные параметры: а,b,c ;

4Выходные параметры: c.

7.Спецификация процедуры collinearity;

1) Function collinearity(a,b:Coordinates):boolean;

2Назначение: возвращает collinearity:=истина , если векторы а и b коллинеарные, иначе- collinearity:=ложь ;

3Входные параметры: a,b;

4Выходные параметры: -.

5 возврат : collinearity

9.Спецификация процедуры MixeMult;

1) Function MixeMult(a,b,c:Coordinates):real

2Назначение: возвращает MixeMult:= значение смешанного произведения векторов а и b

3Входные параметры: a,b;

4Выходные параметры: -.

5Возврат : MixeMult

10.Спецификация процедуры coplanarity;

1) Function coplanarity(a,b,c:Coordinates):boolean

2Назначение: возвращает coplanarity :=истина ,если векторы а,b и c компланарны,иначе- coplanarity :=ложь .

3Входные параметры: a,b,c;

4Выходные параметры: -.

Спецификация подпрограмм для определения вершин пирамиды

1.Спецификация процедуры ploskost

1) Procedure ploskost(a,b,c:coordinates;var ax,bx,cx,dx:real);;

2) Назначение: Строит по 3-м точкам уравнение плоскости вида Ax+By+Cz+D=0 и заносит в ax,bx,cx,dx соответствующие коэффициенты

3) Входные параметры:a,b,c,ax,bx,cx,dx;

4) Выходные параметры: ax,bx,cx,dx.

2.Спецификация функции proverka_na_ploskost;

1) function proverka_na_ploskost(var P:P_descriptor;var mno:mnoj; n:byte):boolean;;

2) Назначение: проверяет условие принадлежности n точек(указатели которых хранятся в множестве mno) к плоскости ,построенной с помощью процедуры ploskost,возращает значение истины в случае удачной проверки, иначе-ложь;

3) Входные параметры: P,mno,n;

4) Выходные параметры: P,mno.

5) Возврат : f

3.Спецификация функции Vypuklost;

1) Function Vypuklost(var P:P_descriptor;mno:mnoj;n:byte):boolean;;

2) Назначение: Проверяет многоугольник на выпуклость, путем перебора n точек из множества mno ,формированием их в векторы и последующим векторным перемножением . Возвращает значение истины, если при все N точках знак векторного умножения сохраняется, иначе -ложь;

3) Входные параметры: P,mno,n;

4) Выходные параметры: P.

5) Возврат : Q

4.Спецификация функции FinDaPyramid;

1) Procedure FinDaPyramid(var P:P_descriptor;mno:mnoj);

2) Назначение: определяет вершины пирамиды с выпуклым основанием и выводит на дисплей, если же нет решений -выводит соотсветсвующее сообщение ;

3) Входные параметры: P,mno,n;

4) Выходные параметры: P,mno.

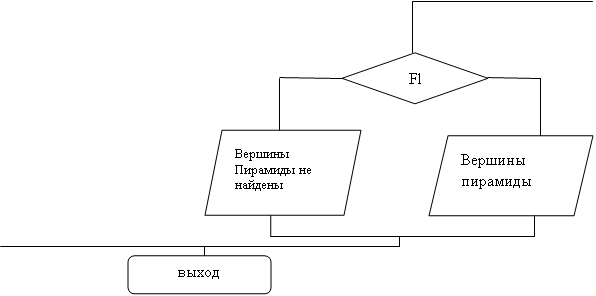
Блок-схема

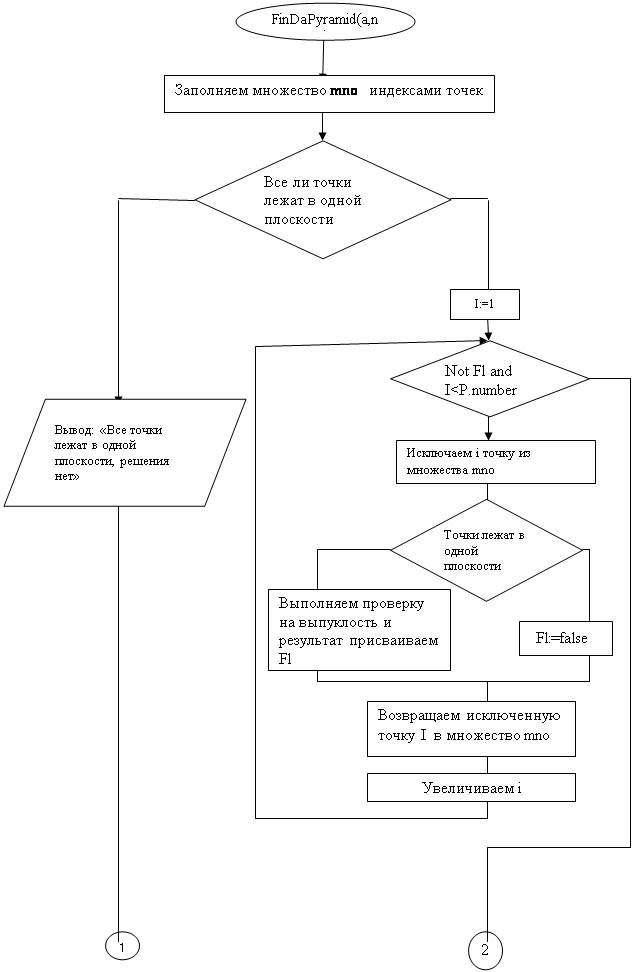
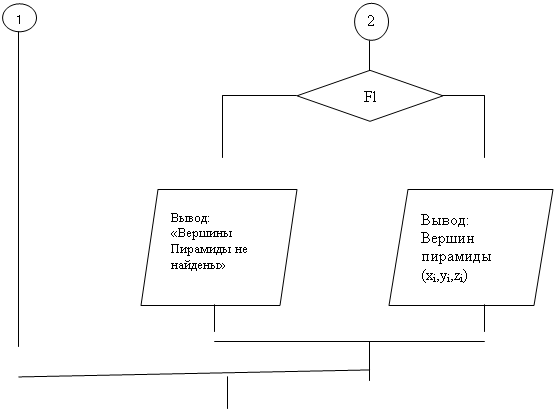Тестовые Данные

-Введем 5 точек

Точка 1(2,-1,-1)

Точка 2(1, 2, 3)

Точка 3(4, 1 1)

Точка 4(0, 1, 2)

Точка 5(7, 1, 1)

-Построим по 3-м точкам уравнение плоскости

Уравнение каждой плоскости имеет вид: Ax + By + Cz + D = 0. Так что наша задача по заданным координатам 3-ех точек плоскости найти коэффициенты A, B, C и D. Эти коэффициенты находятся по формулам:

где x, y, z - координаты наших точек, а 1-2-3 это номера точек A-B-C.

Соответственно находим эти коэффициенты и подставляем их в формулу

--В итоге, получаем уравнение вида Ax + By + Cz + D = 0.

A = -2

B = 10

C = -8

- D = -6

Подставим коэффициенты. Уравнение плоскости:

-2 x + 10 y - 8 z + 6 = 0

Далее, проверим 4 и 5 точку на принадлежность к этой плоскости:

Берем точку 4(0, 1, 2) и подставляем в уравнение -2 x + 10 y - 8 z + 6 = 0

-2(0)+10(1)-8(2)+6=0

0=0

Точка 4 принадлежит плоскости.

Берем точку 5(7, 1, 1) и подставляем в уравнение -2 x + 10 y - 8 z + 6 = 0

-2(7)+10(1)-8(1)+6=0

-6<>0

Точка 5 не лежит в плоскости.

-Далее проверим многоугольник на выпуклость.

Одним из критериев выпуклости является следующее. Многоугольник будет выпуклым, если для векторов, составляющих его периметр, выполняется условие: векторные произведение соседних векторов должны иметь одинаковый знак.

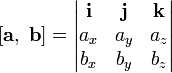
После последовательного выполнения векторного произведения, видим, что многоугольник выпуклый следовательно, данные 5 точек являются вершинами пирамиды с выпуклым основанием, вершины пирамиды:

(2,-1,-1)

(1, 2, 3)

(4, 1, 1)

(0, 1, 2)

(7, 1, 1)

(интерфейс программы)

$Описание: C:\Documents and Settings\Asus\Рабочий стол\курсовой\3.JPG$

(ввод точек)

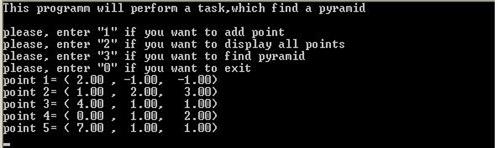
$Описание: C:\Documents and Settings\Asus\Рабочий стол\курсовой\1.JPG$

(вычисление вершин пирамиды с выпуклым основанием и вывод их на дисплей)

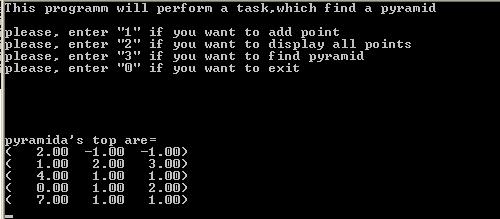
$Описание: C:\Documents and Settings\Asus\Рабочий стол\курсовой\2.JPG$

Заключение

пирамида вершина подпрограмма вектор

В курсовом проекте было предусмотрено следующее:

• создание библиотеки для работы с векторами в пространстве ;

• определение вершин пирамиды в с выпуклым основанием;

Список используемой литературы

1) Брусенцева В.С. Конспект лекций по программированию

2) Фаронов В. С. Turbo Pascal. Начальный курс. Учебное пособие. - М.: Нолидж»,1998 – 616 с.

3) Привалов И.И .Аналитическая геометрия. Учебник издательство «Лань» -304с .

4) Соболь Б.В. Практикум по высшей математике. издательство Ростов. 2006-640с

Приложение

Текст программ

Модуль MyUnit;

Unit MyUnitVector;

interface

Const {константы ошибок}

ListOk=0;

ListNotMem=1;

ListUnder=2;

ListEnd=3;

Type

mnoj=set of byte;

{Определение типов}

Coordinates=record {коориднаты}

x,y,z:real;

end;

P_Points=^point; {Описание типа Points}

point=record

data:Coordinates;

Next:P_Points;

end;

P_Descriptor=record {Дескриптор для работы со списком точек}

Start,Ptr:P_Points;

Number:Word;

end;

P_Vectors=^Vector; {Описание типа Vector}

Vector=record

data:Coordinates;

Next:P_Vectors;

end;

V_Descriptor=record {Дескриптор для работы со списком векторов}

V_Start,V_Ptr:P_Vectors;

V_Number:Word;

end;

Var

ListError:0..3; mno:mnoj;

{подпрограммы для формирования списка хранения и обработки списка векторов}

Procedure InitListOfVectors(var V:V_Descriptor);

Procedure PutVector(var V:V_Descriptor;c:Coordinates);

procedure CreateVector (a,b:Coordinates;var c:Coordinates);

Procedure WriteVectors(var V:V_Descriptor);

Procedure BeginOfVectors(var V:V_Descriptor);

{Подрограммы для работы с векторами}

Procedure AdditionVectors(a,b:Coordinates;var c:Coordinates);

Procedure MultOnNumber (Number:real; a:Coordinates;var c:Coordinates);

Function lengthOfVector(a:Coordinates):real;

Function Scalar(a,b:Coordinates):real;

Function angle(a,b:coordinates):real;

Function projection(a,b:coordinates):real;

Procedure VECTMult(a,b:Coordinates;var c:Coordinates);

Function collinearity(a,b:Coordinates):boolean;

Function MixeMult(a,b,c:Coordinates):real;

Function coplanarity(a,b,c:Coordinates):boolean;

{Подпрограммы для нахождения пирамиды в пространстве}

Procedure FinDaPyramid(var P:P_descriptor;mno:mnoj);

Procedure ploskost(var P:P_descriptor;a,b,c:coordinates;var ax,bx,cx,dx:real);

function proverka_na_ploskost(var P:P_descriptor;var mno:mnoj; n:byte):boolean;

Function Vypuklost(var P:P_descriptor;mno:mnoj;n:byte):boolean;

function Sign(T:real):byte;

{подпрограмм для формирования списка хранения и обработки точек}

Procedure InitListOfPoint(var P:P_Descriptor);

Procedure PutPoint(var P:P_Descriptor);

Procedure WritePoints(var P:P_Descriptor);

Procedure BeginOfPoints(var P:P_Descriptor);

Procedure ReadPoint(var P:P_Descriptor;var a:Coordinates);

Procedure MovePtrOfPoints(var P:P_Descriptor);

Procedure MoveToPoints(var P:P_Descriptor; n:word);

Procedure ClearMem(var P:P_Descriptor;var V:V_Descriptor);

Implementation

Procedure InitListOfVectors;

Begin

If MaxAvail<sizeOf(Vector) Then

ListError:=ListNotMem

else

begin

ListError:=ListOk;

V.V_Number:=0;

New(V.V_start);

V.V_Ptr:=V.V_Start;

end;

End;

Procedure PutVector;

var buf:P_Vectors;

Begin

If MaxAvail<sizeOf(Vector) Then

ListError:=ListNotMem

else

begin

ListError:=ListOk;

V.V_Ptr:=V.V_start;

New(Buf);

buf^.data:=c;

buf^.next:=V.V_Ptr^.next;

V.V_Ptr^.next:=buf;

V.V_Number:=V.V_number+1;

end;

procedure createVector;

begin

with c do

begin

x:=a.x-b.x;

y:=a.y-b.y;

z:=a.z-b.z;

end;

Procedure WriteVectors;

var index:word;

begin

If V.V_Number=0 then

ListError:=ListUnder

else

index:=1;

beginOfVectors(V);

while (V.V_Ptr^.next<>V.V_Start)and(index<=V.V_number) do

begin

writeln('Vector ',index,'= (',V.V_Ptr^.data.x:5:2,' , ',V.V_Ptr^.data.y:5:2,', ',V.V_Ptr^.data.z:5:2,') ');

V.V_Ptr:=V.V_Ptr^.next;

inc(index);

end;

Procedure BeginOfVectors;

begin

V.V_Ptr:=V.V_start^.next;

end;

{Процедуры на свойства векторов}

Procedure AdditionVectors;

begin

with c do

begin

x:=a.x+b.x;

y:=a.y+b.y;

z:=a.z+b.z;

end;

Procedure MultOnNumber;

begin

with c do

begin

x:=number*a.x;

y:=number*a.y;

z:=number*a.z;

end;

Function lengthOfVector;

begin

lengthOfVector:=sqrt(sqr(a.x)+sqr(a.y)+sqr(a.z));

end;

Function Scalar;

begin

Scalar:=a.x*b.x+a.y*b.y+a.z*b.z;

end;

Function angle;

begin

Angle:= arccos(scalar(a,b))/(lengthOf Vector(a)*lengthOfVector(b));

end;

Function projection;

begin

projection:=(lengthOfVector(a)*lengthOfVector(b)*angle(a,b));

end;

Procedure VECTMult;

begin

with c do

begin

x:=a.y*b.z-b.y*a.z;

y:=a.z*b.x-b.z*a.z;

z:=a.x*b.y-b.x*a.y;

end;

Function collinearity;

begin

if ((a.x/b.x)=(a.y/b.y))and((a.y/b.y)=(a.z/b.z)) then

collinearity:=true

else

collinearity:=false;

end;

Function MixeMult;

begin

MixeMult:=a.x*b.y*c.z+a.y*b.z*a.x+a.z*b.x*c.z-a.z*b.y*c.x-a.y*b.x*c.z-a.x*b.z*c.y;

end;

Function coplanarity;

begin

if MixeMult(a,b,c)=0 then

coplanarity:=true

else

coplanarity:=false; end;

{Подпрограммы для нахождения пирамиды}

Procedure ploskost;

var

j:word;

Begin

Ax:=(1*b.y*c.z)+(1*c.y*a.z)+(a.y*b.z*1)-(a.z*b.y*1)-(1*a.y*c.z)-(c.y*b.z*1);

Bx:=(a.x*1*c.z)+(1*b.z*c.x)+(b.x*1*a.z)-(a.z*1*c.x)-(b.x*1*c.z)-(1*b.z*a.x);

Cx:=(a.x*b.y*1)+(b.x*c.y*1)+(a.y*1*c.x)-(1*b.y*c.x)-(c.y*1*a.x)-(b.x*a.y*1);

Dx:=-((a.x*b.y*c.z)+(b.x*c.y*a.z)+(a.y*b.z*c.x)-(c.y*b.z*a.x)-(a.z*b.y*c.x)-(b.x*a.y*c.z));

if (ax=0)and(bx=0)and(cx=0) then

writeln('lejat na odnoi pr9mou');

end;

Procedure FindaPyramid;

var

i,k:word;

f,fl:boolean;

a:coordinates;

begin

mno:=[];

for i:=1 to p.number do

mno:=mno+[i];

f:=proverka_na_ploskost(p,mno,p.number);

if f then writeln('resheni9 net..vse to4ki lejat v ploskosti')

else

begin

i:=1;

fl:=false;

while (not fl)and(i<=p.number) do

begin

mno:=mno-[i];

writeln;

if proverka_na_ploskost(p,mno,p.number-1) then

fl:=Vypuklost(p,mno,p.number-1)

else

fl:=false;

mno:=mno+[i];

i:=i+1;

end;

if fl then

begin

writeln('pyramida''s top are= ');

for i:=1 to p.number do

begin

movetopoints(p,i);

readpoint(p,a);

Writeln('( ',a.x:6:2,' ',a.y:6:2,' ',a.z:6:2,') ');

end;

end

else writeln('pyramida is not found ');

end;

function proverka_na_ploskost;

var

ax,bx,cx,dx:real;

i:word;

a,t1,t2,t3:coordinates;

f:boolean;

begin

i:=1;

while not( i in mno) do i:=i+1;

movetopoints(p,i);

readpoint(p,t1);

i:=i+1;

while not( i in mno) do i:=i+1;

movetopoints(p,i);

readpoint(p,t2);

i:=i+1;

while not( i in mno) do i:=i+1;

movetopoints(p,i);

readpoint(p,t3);

ploskost(p,t1,t2,t3,ax,bx,cx,dx);

f:=true;

while (i<=n)and f do

begin

i:=i+1;

while not( i in mno) do i:=i+1;

movetopoints(p,i);

readpoint(p,a);

if ax*a.x+bx*a.y+cx*a.z+dx=0 then

begin

f:=true;

end

else

begin

f:=false;

end;

proverka_na_ploskost:=f;

end;

Function Vypuklost;

var

i,j,k:byte;

Q:boolean;

T,Z,Px:real;

a,b,v1,v2:coordinates;

begin

i:=1;

while not( i in mno) do i:=i+1;

movetopoints(p,i);

readpoint(p,a);

k:=0;

while (k<>n) do

begin

if (i in mno) then inc(k);

inc(i);

end;

movetopoints(p,i);

readpoint(p,b);

inc(i);

createVector(a,b,V1);

createVector(a,b,V2);

T:=(v1.y*v2.z-v2.y*v1.z)-(v1.x*v2.z-v2.y*v1.z)+(v1.x*v2.y-v2.x*v1.y);

Z:=Sign(T);

Px:=1.0;

j:=1;

Q:=true;

While (Q and (j<n))do

begin

while not( j in mno) do j:=j+1;

movetopoints(p,j);

readpoint(p,a);

inc(j);

while not( j in mno) do j:=j+1;

movetopoints(p,j);

readpoint(p,b);

createVector(a,b,V1);

createVector(a,b,V2);

T:=(v1.y*v2.z-v2.y*v1.z)-(v1.x*v2.z-v2.y*v1.z)+(v1.x*v2.y-v2.x*v1.y);

Px:=Px*Z*Sign(T);

if (Px<0) then Q:=false;

inc(i);

end;

Vypuklost:=Q;

end;

function Sign;

begin

if t=0 then

Sign:=1

else

sign:=round(t/abs(t));

end;

{Подпрограммы для обрабоки списка точек}

Procedure InitListOfPoint;

Begin

If MaxAvail<sizeOf(point) Then

ListError:=ListNotMem

else

begin

ListError:=ListOk;

P.Number:=0;

New(P.start);

P.Ptr:=P.Start;

end;

End;

Procedure PutPoint;

var buf:P_Points;

Begin

If MaxAvail<sizeOf(point) Then

ListError:=ListNotMem

else

begin

ListError:=ListOk;

P.ptr:=P.start;

New(Buf);

write('Input point = ');

readln(buf^.data.x,buf^.data.y,buf^.data.z);

buf^.next:=P.Ptr^.next;

P.Ptr^.next:=buf;

P.Number:=P.number+1;

end;

Procedure WritePoints;

var index:word;

begin

If P.Number=0 then

ListError:=ListUnder

else

index:=1;

beginOfPoints(P);

while (P.Ptr^.next<>P.Start)and(index<=P.number) do

begin

writeln('point ',index,'= (',P.Ptr^.data.x:5:2,' , ',P.Ptr^.data.y:5:2,', ',P.Ptr^.data.z:5:2,') ');

P.Ptr:=P.Ptr^.next;

inc(index);

end;

Procedure BeginOfPoints;

begin

P.Ptr:=P.start^.next;

end;

Procedure ReadPoint;

begin

if P.Number=0 then

ListError:=ListUnder

else

begin

ListError:=ListOk;

a:=P.Ptr^.data;

end;

procedure MovePtrOfPoints;

begin

P.Ptr:=P.Ptr^.next;

end;

Procedure MoveToPoints;

var i:word;

begin

IF n>P.Number then

ListError:=ListUnder

else

begin

ListError:=ListOk;

P.Ptr:=P.start;

i:=0;

While i<n do

begin

P.Ptr:=P.Ptr^.next;

i:=i+1;

end;

Procedure ClearMem;

var

P_i,P_j:P_Points;

V_i,V_j:P_Vectors;

Begin

P_i:=P.start^.next;

V_i:=V.V_start^.next;

dispose(P.start);

dispose(V.V_start);

While (P.Number<>0) do

begin

P.Number:=P.number-1;

P_j:=P_i;

P_i:=P_i^.next;

dispose(P_j);

end;

dispose(V_j);

end;

end.

Текст основной программы

program FindPyramid;

uses MyUnitVector,crt;

var D_Vector:V_Descriptor;

D_point :P_Descriptor;

a,b,c:Coordinates;

ch:char;

sum,sum2:real;

n1,n2:word;

begin

clrscr;

initlistOfPoint(D_point);

InitListOfVectors(D_vector);

repeat

writeln('This programm will perform a task,which find a pyramid ');

writeln;

writeln('please, enter "1" if you want to add point');

writeln('please, enter "2" if you want to display all points');

writeln('please, enter "3" if you want to find pyramid');

writeln('please, enter "0" if you want to exit');

ch:=readkey;

Case ch of

#49 : PutPoint(D_point);

#50 : begin

WritePoints(D_point);

readkey;

end;

#51 : begin

FinDaPyramid(D_point,mno);

readkey;

end;

c lrscr;

until ch=#48;

clearmem(D_point,D_vector);

writeln('Error=',ListError);

readkey;

end.