
Рефераты по рекламе
Рефераты по физике
Рефераты по философии
Рефераты по финансам
Рефераты по химии
Рефераты по хозяйственному праву
Рефераты по экологическому праву
Рефераты по экономико-математическому моделированию
Рефераты по экономической географии
Рефераты по экономической теории
Рефераты по этике
Рефераты по юриспруденции
Рефераты по языковедению
Рефераты по юридическим наукам
Рефераты по истории
Рефераты по компьютерным наукам
Рефераты по медицинским наукам
Рефераты по финансовым наукам
Рефераты по управленческим наукам
Психология педагогика
Промышленность производство
Биология и химия
Языкознание филология
Издательское дело и полиграфия
Рефераты по краеведению и этнографии
Рефераты по религии и мифологии
Рефераты по медицине
Курсовая работа: Проектирование и расчёт полосного фильтра
Курсовая работа: Проектирование и расчёт полосного фильтра
Проектирование и расчёт полосного фильтра
Реферат
Курсовая работа: 18с., 8 рис., 2 табл., 3 источника.
Объект исследования – активный полосовой фильтр на операционном усилителе.
Цель работы – расчёт и синтез схемы полосового фильтра на интегральном операционном усилителе, анализ амплитудно-частотной характеристики полученного устройства.
Метод исследования – формирование виртуальной модели фильтра, определение электрических параметров (по средствам ЭВМ).
Спроектирован фильтр на
операционном усилителе с многопетлевой обратной связью. Устройство
характеризуется следующими параметрами: частота среза ![]() , полоса пропускания Δf=250 Гц, коэффициентом передачи в
полосе пропускания
, полоса пропускания Δf=250 Гц, коэффициентом передачи в
полосе пропускания ![]() , наклон АЧХ 40(дБ/дек).
Установлено, что выбранная схема фильтра является одной из наиболее дешёвых в
реализации, при соблюдении предъявляемых к ней требований.
, наклон АЧХ 40(дБ/дек).
Установлено, что выбранная схема фильтра является одной из наиболее дешёвых в
реализации, при соблюдении предъявляемых к ней требований.
Ключевые слова:
ОПЕРАЦИОННЫЙ УСИЛИТЕЛЬ, ПОЛОСОВОЙ ФИЛЬТР, АМПЛИТУДНО-ЧАСТОТНАЯ ХАРАКТЕРИСТИКА, ЧАСТОТА СРЕЗА, ПОЛОСА ПРОПУСКАНИЯ, ОТРИЦАТЕЛЬНАЯ ОБРАТНАЯ СВЯЗЬ.
Содержание
Введение
1 Анализ технического задания
2 Синтез схемы и расчет элементов фильтра
3 Расчет АЧХ фильтра на ЭВМ
4 Подбор элементов для схемы
Выводы
Список использованных источников
Введение
Цепи фильтрации сигналов – важная и неотъемлемая часть многих систем связи и электрических контрольно-измерительных устройств. Они служат для формирования частотных каналов в системах коммутации, разделения и преобразования электрических сигналов.
В большинстве случаев электрический фильтр представляет собой частотно-избирательное устройство. Следовательно, он пропускает сигналы определённых частот и задерживает или ослабляет сигналы других частот. Наиболее общими типами частотно-избирательных фильтров являются фильтры нижних частот (которые пропускают низкие частоты и задерживают высокие частоты), фильтры верхних частот (которые пропускают высокие частоты и задерживают низкие частоты), полосно-пропускающие фильтры (которые пропускают полосу частот и задерживают те частоты, которые расположены выше или ниже этой полосы) и полосно-заграждающие фильтры (которые задерживают полосу частот и пропускают те частоты, которые расположены выше или ниже этой полосы).
На практике невозможно реализовать идеальную амплитудно-частотную характеристику фильтра, поскольку требуется сформировать очень узкую переходную область. Следовательно, основная проблема при конструировании фильтра заключается в приближении реализованной реальной характеристики с заданной степенью точности к идеальной.
1. Анализ технического задания
Фильтры - это частотно-избирательные устройства, которые пропускают или задерживают сигналы, лежащие в определенных полосах частот. До 60-х годов для реализации фильтров применялись, в основном, пассивные элементы, т.е. индуктивности, конденсаторы и резисторы. Основной проблемой при реализации таких фильтров оказывается размер катушек индуктивности (на низких частотах они становятся слишком громоздкими). С разработкой в 60-х годах интегральных операционных усилителей появилось новое направление проектирования активных фильтров на базе ОУ. В активных фильтрах применяются резисторы, конденсаторы и усилители (активные компоненты), но в них нет катушек индуктивности. В дальнейшем активные фильтры почти полностью заменили пассивные. Сейчас пассивные фильтры применяются только на высоких частотах (выше 1 МГц), за пределами частотного диапазона большинства ОУ широкого применения. Но даже во многих высокочастотных устройствах, например в радиопередатчиках и приемниках, традиционные пассивные RLC-фильтры заменяются кварцевыми фильтрами и фильтрами на поверхностных акустических волнах.
Сейчас во многих случаях аналоговые фильтры заменяются цифровыми. Работа цифровых фильтров обеспечивается, в основном, программными средствами, поэтому они оказываются значительно более гибкими в применении по сравнению с аналоговыми. С помощью цифровых фильтров можно реализовать такие передаточные функции, которые очень трудно получить обычными методами. Тем не менее, цифровые фильтры пока не могут заменить аналоговые во всех ситуациях, поэтому сохраняется потребность в наиболее популярных аналоговых фильтрах — активных RС-фильтрах.
Фильтры можно классифицировать по их частотным характеристикам, что в условном виде показано на рис. 1.1. На этом рисунке изображены характеристики фильтра нижних частот (ФНЧ), фильтра верхних частот (ФВЧ), полосового фильтра (ПФ), полосно-подавляющего фильтра (ППФ) и фильтра - "пробки" (режекторного фильтра - РФ). Характеристика фазового фильтра (ФФ) на рисунке не показана, т.к. его коэффициент передачи не изменяется с частотой. Основная функция любого фильтра заключается в том, чтобы ослабить сигналы, лежащие в определенных полосах частот, внести в них различные фазовые сдвиги или ввести временную задержку между входным и выходным сигналами.
С помощью активных RС-фильтров нельзя получить идеальные формы частотных характеристик в виде показанных на рис. 1.1 прямоугольников со строго постоянным коэффициентом передачи в полосе пропускания, бесконечным ослаблением в полосе подавления и бесконечной крутизной спада при переходе от полосы пропускания к полосе подавления. Проектирование активного фильтра всегда представляет собой поиск компромисса между идеальной формой характеристики и сложностью ее реализации. Это называется "проблемой аппроксимации". Во многих случаях требования к качеству фильтрации позволяют обойтись простейшими фильтрами первого или второго порядков. Проектирование фильтра в этом случае сводится к выбору схемы с наиболее подходящей конфигурацией и последующему расчету значений номиналов элементов для конкретных частот.
Однако бывают ситуации, когда требования к фильтрации сигнала могут оказаться гораздо более жесткими, и могут потребоваться схемы фильтров с характеристиками более высоких порядков, чем первый или второй.
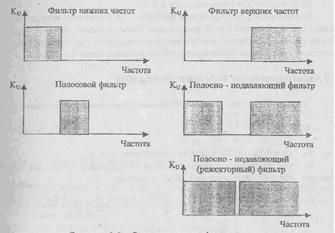
Рисунок 1.1- Основные типы фильтров.
Реальные характеристики фильтров, а именно нижних частот, верхних частот и полосового фильтра, - показаны на рисунке 1.2.
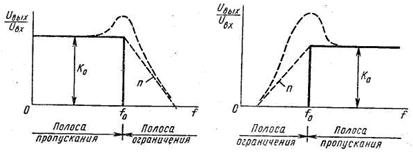
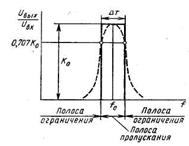
Рисунок 1.2 – АЧХ фильтров.
На этих рисунках сплошными линиями изображены идеальные характеристики фильтров. Пунктирные линии показывают отклонение реальных характеристик от идеальных. Основными параметрами фильтров нижних и верхних частот являются частота среза f0, коэффициент передачи в полосе пропускания Ко, наклон АЧХ в полосе ограничения п и неравномерность АЧХ в полосе пропускания. Для полосовых фильтров по аналогии с избирательными усилителями вводят понятие добротности Q и усиления Ко на частоте f0.
2. Синтез схемы и расчет элементов фильтра
2.1 Исходные данные и требования для проектирования фильтра
| Тип фильтра – ПФ | ||
|
Частота среза, f0 |
5000 | Гц |
|
Коэффициент передачи в полосе пропускания, К0 |
6 | |
| Наклон АЧХ в полосе ограничения, n | 40 | дБ/дек |
| Неравномерность АЧХ в полосе пропускания, ΔК | 20 | дБ |
| Полоса пропускания, Δf | 250 | Гц |
2.2 Разработка функциональной схемы
На рис. 2.1 приведена структурная схема фильтра с многопетлевой обратной связью. Каждый пассивный двухполюсный элемент в этой схеме может быть либо резистором, либо конденсатором.
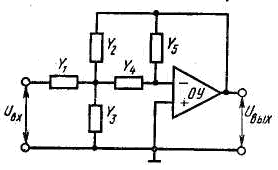
Рисунок 2.1 – структурная схема фильтра
Передаточная функция для данной схемы имеет вид
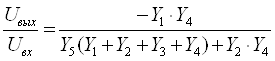 (2.1)
(2.1)
Для того чтобы схема на рис. 2.1 выделяла полосу частот, передаточную функцию (2.1) необходимо привести к передаточной функции, соответствующей полосовому звену второго порядка:
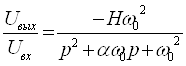 (2.2)
(2.2)
где ωо = 2лf0, H =α·К0.
Сравнивая выражения (2.1) и (2.2), нетрудно заметить, что, для того чтобы числитель не был функцией р, в качестве У1 и У4 должны использоваться резистивные проводимости; для того чтобы получить член с р2 в знаменателе, в качестве У3 и У5 должны использоваться емкостные проводимости; для того чтобы получить в знаменателе член, независимый от р, в качестве У2 должна использоваться резистивная проводимость.
Итак, однозначно определяются пассивные элементы схемы на рис. 2.1:
Y1=1/R1, Y2= pC1, Y3=1/R2, Y4= pC2, Y5=1/R3.
Схема полученного полосового фильтра приведена на рис. 2.2.
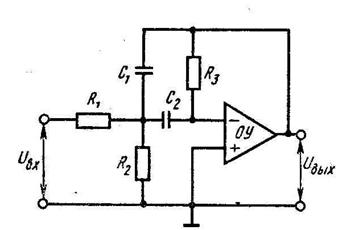
Рисунок 2.2 – Схема полосового фильтра
Передаточная функция имеет вид
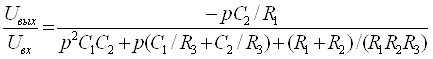 (2.3)
(2.3)
Сравнивая последнее выражение с (2.2), получаем соотношения, необходимые для расчета фильтра:
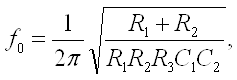
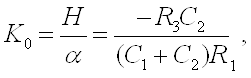
![]()
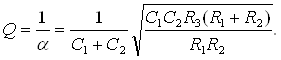 (2.4)
(2.4)
В том
случае, если ![]() и
и ![]() , имеем:
, имеем:
![]() (2.5)
(2.5)
Отсюда
ясно, что для получения больших значений добротности значения R1, R2, R3 должны быть по возможности разнесены. Порядок расчета
фильтра с заданной добротностью таков. Выбираем величину С1=С2=С,
определяем коэффициент К=2πf0C и находим остальные элементы схемы
по формулам:![]()
![]() (2.6)
(2.6)
2.3 Расчет элементов схемы
Выбираем схему фильтра на основе ОУ с многопетлевой обратной связью (см. рис. 2.2).
Выбираем ОУ по частоте единичного усиления fТ ОУ ≥ f0 К0 = 15 кГц.
Для ОУ типа К140УД6 fТ =1МГц, т.е. последнее неравенство выполняется с запасом. Схема электрическая принципиальная данного ОУ представлена на рисунке 2.3. Паспортные данные выбранного ОУ представлены в таблице [1, приложение А].
По справочнику, RВХ ОУ = 1000 кОм, RВЫХ ОУ = 150 Ом, т.е. номиналы резисторов в схеме фильтра должны находится в пределах от 1,5 к Ом до 100 к Ом.
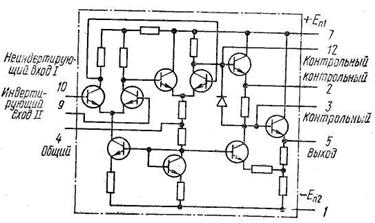
Рисунок 2.3 – Схема операционного усилителя К140УД6.
Зададимся значением емкости С2 = 500 пФ, при этом отметим, что выбранная величина существенно больше возможных паразитных емкостей в схеме.
Найдем значение вспомогательного коэффициента
![]()
Отсюда
величина емкости С1 при ![]()
![]() пФ.
пФ.
Определим значения резисторов схемы фильтра:
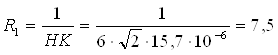 кОм;
кОм;
 кОм;
кОм;
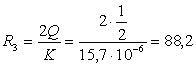 кОм.
кОм.
Проверяем полученное значение частоты:
 Гц
Гц
и коэффициента усиления в полосе пропускания:
![]()
3. Расчет АЧХ фильтра на ЭВМ
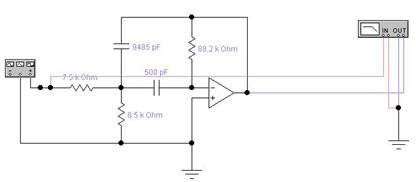
Рисунок 3.1 – Полосовой фильтр. Схема электрическая принципиальная.
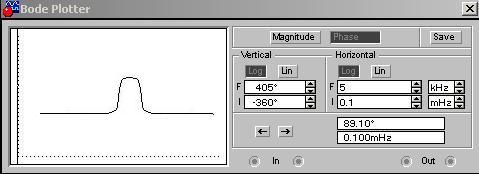
Рисунок 3.2 – Полученная осциллограмма полосового фильтра
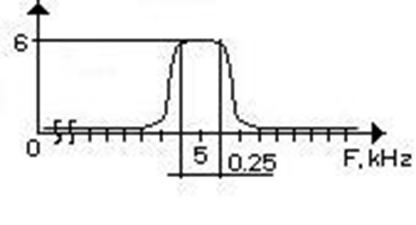
Рисунок 3.3 – АЧХ полосового фильтра на частоте 5кГц.
4. Подбор элементов для схемы
Для проектируемого фильтра выбираем два керамических конденсатора типа КМ-6. Данный тип конденсаторов может обеспечить необходимую емкость в 500 и 9500 пФ, а также имеет номинальное напряжение при температуре 85 °С 50 В, допустимое отклонение емкости от номинальной составляет 5 и 10 % соответственно.
Для подбора резисторов воспользуемся таблицей [1, приложение Б], где указаны ряды промежуточных значений сопротивлений.
Сопротивление резистора R1 можно обеспечить следующим резистором металлопленочный резистор МЛТ R=7,5 кОм ряд Е24, у которого допустимое отклонение сопротивления от номинального 5%, а предельное рабочее напряжение 350 В.
Резистор R2 состоит из: металлопленочный резистор МЛТ R=8,5 кОм ряд Е24 отклонение сопротивления от номинального 20%, предельное рабочее напряжение 30В.
В качестве резистора R3 берем металлопленочный резистор МЛТ
R=88,2 кОм ряд Е24.
Выводы
В данном курсовом проекте был произведен расчет полосового фильтра, а именно: подобран ОУ типа К140УД6, рассчитаны и подобраны элементы схемы.
Проверка показала, что данный фильтр обеспечивает коэффициент передачи в полосе пропускания К0=6 на частоте f0=5кГц.
При помощи ЭВМ была смоделирована схема фильтра и построена его АЧХ, которая соответствует полосовому фильтру.
Список использованных источников
1. Расчет электронных схем. Примеры и задачи: учеб. Пособие для вузов по спец. электрон. технике. / Г.И. Изъюров, Г.В.Королев и др.- М.: Высшая школа, 2007. – 335с.
2. Джонсон Д, Джонсон Дж. Справочник по активным фильтрам. - М.: Энергоатомиздат, 2003.-128с.
3. Терещук Р.М. и др. Полупроводниковые приемно-усилительные устройства: Справ. Радиолюбителя.- Киев: Наук. думка, 1989,.-800с.