Курсовая работа: Корреляционный анализ солнечной и геомагнитной активностей

ГЛАВНОЕ УПРАВЛЕНИЕ ОБРАЗОВАНИЯ И НАУКИ

ХАРЬКОВСКОЙ ОБЛАСТНОЙ

ГОСУДАРСТВЕННОЙ АДМИНИСТРАЦИИ

ХАРЬКОВСКОЕ ТЕРРИТОРИАЛЬНОЕ ОТДЕЛЕНИЕ

МАЛОЙ АКАДЕМИИ НАУК

ФИЗИКО-МАТЕМАТИЧЕСКОЕ ОТДЕЛЕНИЕ

СЕКЦИЯ АСТРОНОМИИ

КОРРЕЛЯЦИОННЫЙ АНАЛИЗ СОЛНЕЧНОЙ

И ГЕОМАГНИТНОЙ АКТИВНОСТИ

Выполнила:

Пирогова Ульяна Владимировна,

ученица 11 класса ХНУ лицея

Дзержинського района г. Харкова

Научный руководитель:

Грецкий Андрей Михайлович,

кандидат физико-математичских наук,

доцент Харьковского Национального

Университета им. В.Н. Каразина

г. Харьков – 2009

Содержание

Введение

1. Солнечная активность.

1.1 Количественное измерение солнечной активности.

1.2 Классификация групп пятен.

1.3 Астрометрическое наблюдение Солнца относительно Земли.

2. Межпланетная секторная структура

3. Магнитное поле Земли.

3.1 Магнитосферные бури и суббури.

3.2 Единицы напряжённости магнитного поля

3.3 Составляющие магнитного поля

4. Индексы, характеризующие геомагнитные вариации.

5. Постановка задачи.

6. Реализация задачи.

Выводы

Литература

Приложения

Введение

Германский любитель астрономии Генрих Швабе, наблюдавший за солнечным диском с 1826г. по1843г. в поисках новой планеты, заметил 11-летний цикл изменения количества пятен на Солнце. Однако ранее, Питер Горребов (Дания г.Копенгаген), интервал наблюдений которого 1761-1769г., утверждал о периодичности солнечных пятен, связывая их появления с мощными полярными сияниями. В середине 19 в. Иоганн фон Ламон обнаружил увеличение числа магнитных бурь с таким же периодом, а в конце этого же века В.О. Биркелан предположил, что кроме электромагнитного излучения Солнце испускает частицы. Эти и последующие открытия положили начало изучению солнечно-земных связей- разделу науки на стыке геофизики и физики Солнца.[1]

Проявлением солнечно-земных связей является следующая последовательность событий: с возникновения солнечной вспышки в солнечном ветре (СВ) генерируется ударная волна, несколько опережающая плазменное облако; по достижению Земли ударная волна порождает магнитную бурю, а облако плазмы — суббури. Развитие и затухание центра активности также вызывают магнитосферные возмущения. Это обусловлено тем, что подобные процессы приводят к перераспределению магнитных полей и потоков солнечной плазмы, исходящих в межпланетное пространство. Поскольку в различных частях солнечного диска развивается и затухает несколько центров активности , магнитосфера погружена в непрерывно изменяющуюся межпланетную секторную структуру (МСС).В каждой секторной структуре происходит систематическое изменение плотности СВ, его скорости и напряжённости магнитного поля. Неоднородность перечисленных характеристик связана с нестабильной солнечной активностью. Для более глубокого исследования солнечно-земных связей вводятся численные оценки меры солнечных воздействий и земных откликов на них, т.е. специальные индексы.

1. Солнечная активность

Причиной нестабильности активности Солнца является его дифференциальное вращение, которое «вытягивает» погружённые силовые линии магнитного поля Солнца и усиливает его до 2000-4000Гс. Это усиление делает погружённые силовые трубки неустойчивыми, обуславливая их появление над поверхностью фотосферы на гелиографических широтах ±40° и постепенное снижение к экватору. В точках пересечения образуются пятна(первым- ведущее пятно), в областях над ними разогревается хромосфера и корона- образование факелов (флоккул)и протуберанцев (волокон).

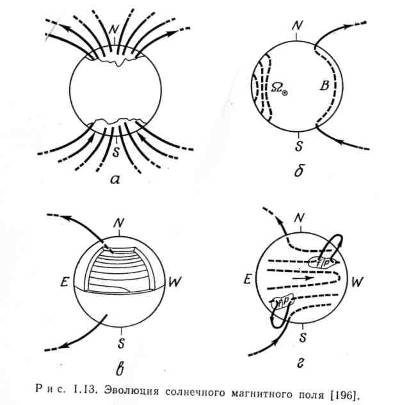
Рис.1 Эволюция солнечного магнитного поля.

Из-за турбулентности, происходящей под фотосферой, магнитное поле центра активности становится сложным и неустойчивым- образуются новые пятна. На широте 15° центр активности достигает максимума, характеризующегося наибольшим числом пятен и солнечными вспышками. Приближаясь к широте 3° центр активности окончательно затухает.[2]

Большую часть времени жизни пятна его магнитное поле остаётся постоянным, в то время как площадь пятна по достижения максимума только убывает. Открыл Коулинг в 1946 году, сравнивая данные о магнитных полях и площади пятен, полученные в Маунт Вилсон, (рис. 2)

Рис.2.

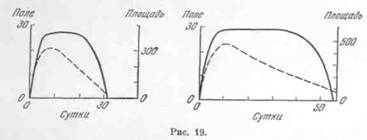
Выведенные кривые являются усреднёнными, в них сглажены флуктуации поля ото дня ко дню, не носящие систематического характера. Следовательно, магнитное поле не создаётся вместе с пятном, а лишь «выходит» на поверхность, а затем опять опускается вниз под фотосферу.[4]

Ранее отмечалось, что при наибольшей концентрации пятен в центре активности возникают солнечные вспышки (эрупции). К их возникновению приводит взаимное движение пятен, при котором происходит изменение потока магнитной индукции, возбуждающие электрическое поле. Это поле ускоряет частицы солнечной плазмы — повышение температуры плазмы. Вспышка характеризуется резким увеличением яркости хромосферы над максимумами центров активости. Ее длительность от 5 до 40 минут, в годы максимума может достигать 3 и более часов. Количество выделяемой энергии может достигать 1033 Дж (≈ 1 млн. водородных бомб). Т.е. эрупции – это сильные взрывы, порождаемые сжатием солнечной плазмы под действием давления магнитных полей.

1.1 Количественное измерение солнечной активности

Для количественной оценки Солнечной активности наиболее часто применяют показатель относительных чисел солнечных пятен, называемых числами Вольфа, вычисляемых по формуле

Rw = k (10g + f),

гдек – коэффициент, зависящий от условий наблюдателя и вида инструмента;

g – количество групп пятен на Солнце;

f – число пятен во всех группах.

Важность этого индекса (Rw) определяется:

1) его простотой;

2) тем, что значения его известны начиная с 1700г. (годичные данные) или с 1749г. (месячные данные);

3) его выдающимся гелиофизическим значением, которое выражается в значении ряда значительных корреляций с индексом W у многих важных геофизических характеристик;

4) он в общем довольно хорошо характеризует общую напряжённость геоактивной ультрафиолетовой радиации Солнца …

Данное определение изъясняет выбор названного индекса и для настоящей работы. К тому же в настоящее время имеются методы прогноза чисел Вольфа, и установлена численная связь, хотя и не очень тесная (коэффициент корреляции между ними порядка 0,85).[3]

Основным рядом Rw считается ряд Цюрихской обсерватории, начатый в 1749г.

1.2 Классификация групп пятен

Хейлом на обсерватории Маунт-Вилсон установлено, что группы пятен могут быть разделены на три класса:

1) Униполярные группы – одиночное пятно или группа пятен, обладающих магнитными полями одной и той же полярности.

2) Биполярные группы, в наиболее простом случае состоят из бинарных пятен (бинарные группы) с противоположной полярностью. Ось группы (линия, соединяющая пятна) составляет небольшой угол с солнечной параллелью. Часто вместо двух пятен мы встречаемся с двумя группами мелких пятен, образующих ведущие и последующие компоненты группы, которые так же, как и отдельные пятна, обладают различной полярностью.

3) Сложные группы пятен состоят из пятен различной полярности, расположенных весьма неправильно.

Униполярные группы представляют собой неразвитые или, наоборот, очень старые группы биполярного типа, в которых одно из пятен заменяется областью противоположной магнитной полярности. Хейл называл такие области «невидимыми пятнами» и установил их присутствие по наличию магнитного поля. Сложные группы, не представляют собой одного целого и возникают как следствие переналожение нескольких биполярных групп. Биполярная группа является основным и наиболее характерным образованием среди групп пятен.

Также Хейл открыл закон смены магнитной полярности биполярных групп, следовательно- и Солнца. В течении 11-летнего цикла солнечной активности все ведущие пятна имеют одинаковую полярность, т.е. все биполярные группы имеют одинаковую ориентировку в долготном направлении. При наступлении нового цикла эта ориентировка меняется на обратную. Данному закону следует ≈ 98% всех биполярных групп — и многие астрономы считают основным 22-летний цикл.[5]

1.3 Астрометрическое наблюдение Солнца относительно Земли

В связи с неравномерным движением вещества на Солнце различные его зоны вращаются вокруг оси с различными периодами. Для точек экватора сидерический период составляет 25 суток, а в близи полюсов он достигает 30 суток. Вследствие движения Земли вокруг Солнца его вращение представляется земному наблюдателю несколько замедленным: период вращения на экваторе составляет 27 суток, а у полюсов – 32 суток (синодический период вращения).

Поскольку Солнце вращается не как твёрдое тело, систему гелиографических координат нельзя жёстко связать со всеми точками поверхности. Условно гелиографические меридианы жёстко связываются с точками, имеющими географические широты В= ±16°. Для них сидерический период обращения составляет 25,38 суток, а синодический равен 27,28 суток. За начальный гелиографический меридиан принят тот, который 1 января 1954 года в 0h по всемирному времени проходил через точку пересечения солнечного экватора с эклиптикой.[6]

2. Межпланетная секторная структура

Конфигурация межпланетных магнитных полей (ММП) подобна спирали Архимеда. Вектор магнитного поля В имеет радиальную компоненту Вr, направленную либо внутрь, либо наружу (к Солнцу или от Солнца), и азимутальную компоненту Вφ. Межпланетное пространство разделено на чередующиеся спиральные сектора, в каждом из которых

радиальная компонента направлена либо наружу, либо внутрь (рис.3). Эта секторная структура вращается вместе с Солнцем. По данным наблюдений межпланетных полей (с помощью ракет) период вращения Солнца может быть подразделён на несколько субпериодов, каждый продолжительностью в несколько суток, в течение которых радиальная компонента направлена преимущественно наружу или внутрь. Такая последовательность субпериодов может наблюдаться в продолжении нескольких оборотов Солнца, свидетельствуя о высокой степени стабильности секторной структуры. СВ движется наружу так, как если бы магнитного поля не было. В системе отсчёта, жёстко связанной с Солнцем, магнитные силовые линии параллельны или антипараллельны направлению СВ.

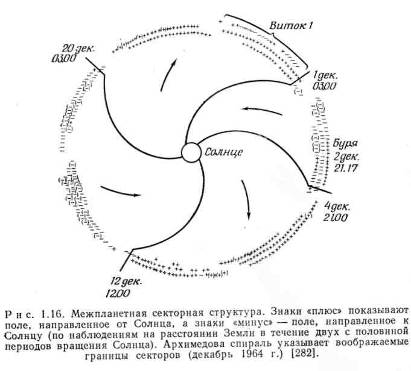
Рис.3 Межпланетная секторная структура. Знаки «плюс» показывают поле направленное от Солнца, а знаки «минус» - поле, направленное к Солнцу (по наблюдениям на расстояниям Земли в течении е двух с половиной периодов вращения Солнца. Архимедова спираль указывает воображаемые границы секторов (декабрь 1964г.).

В пределах каждого сектора скорость СВ и плотность частиц систематически изменяется (рис.4).

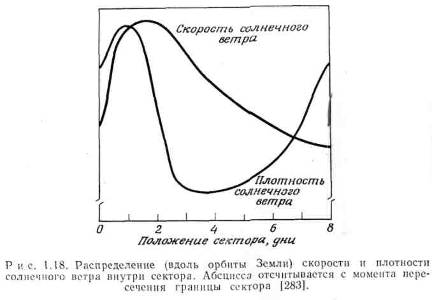
Рис.4 Распределение (вдоль орбиты Земля) скорости и плотности солнечного ветра внутри сектора. Абсцисса отсчитывается с момента пересечения границы сектора.

Ракетные наблюдения показывают, резкое увеличение данных параметров на границе сектора. Однако плотность очень быстро уменьшается в конце второго дня после прохождения границ, а затем дня через 2 или 3 начинает медленно расти. Скорость СВ уменьшается медленно на 2 или 3 день после достижения пика. Секторная структура и отмеченные вариации скорости и плотности тесно связаны с умеренной магнитосферными возмущениями Солнца.

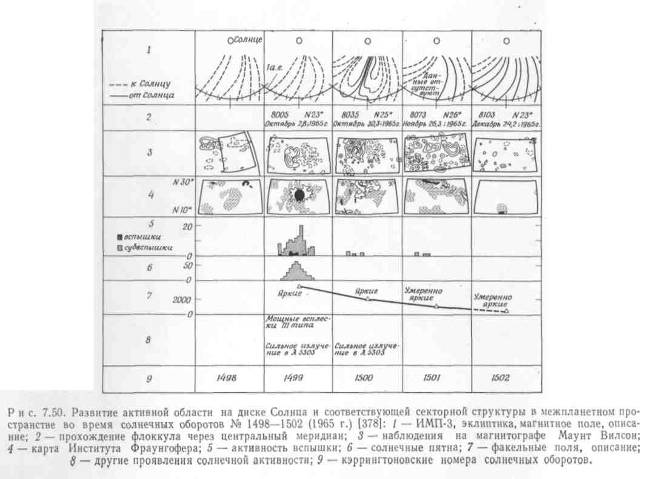
Вилкокс и Несс, сравнив наблюдаемую межпланетную секторную структуру (МСС) с конфигурацией фотосферных магнитных полей, заключили, что фотосферные магнитные поля, находящиеся в поясе гелиографической широты 15°, вытягиваются наружу СВ, образовывая устойчивые и долго живущие крупномасштабные поля малой напряжённости, существующее с другими магнитными полями. Бартельс назвал этот тип гидромагнитной активности М-возмущениями; СВ, ответственный за него, называется М-потоком, а его источник на поверхности Солнца – М-областью. Граница между двумя полярностями М-области проходит приблизительно с севера на юг и полярность не изменяется при пересечении экватора (рис.5).[9]

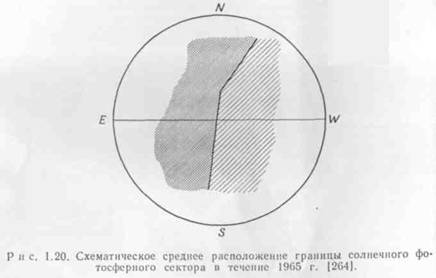
Рис.5 Схематическое среднее расположение границы солнечного фотосферного сектора в течении 1965г.

К развитию нового сектора приводит рост центра активности: на уровне фотосферы вызывает перераспределение магнитного поля и картины потоков СВ.

М-области часто не содержат солнечных пятен, т.к. стремятся избегать области повышенного коронарного излучения.

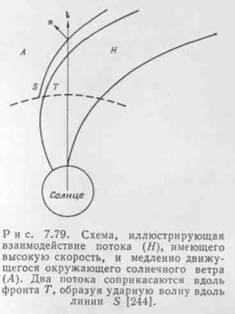
МСС существует даже во время самого спокойного периода 11-летнего цикла солнечной активности. Внутри каждой секторной структуры ее характеристики (скорость, концентрация и напряженность ММП) систематически изменяются, и достигают своих максимальных значений вблизи ведущей границы сектора. Следовательно, ведущий фронт (кривая Т на рис.7) создает радиальную силу на тыловой стороне секторной структуры (впереди неё). Такое взаимодействие может сформировать в секторной структуре ударную волну (кривая S на рис.7). Вследствие чего ведущие границы МСС имеют характеристики тангенциального разрыва.

Рис.7 Схема, иллюстрирующая взаимодействие потока (Н), имеющего высокую скорость, и медленно движущегося окружающего солнечного ветра (А). Два потока соприкасающегося вдоль фронта Т, образую ударную волну вдоль линии S.

Секторная структура довольно устойчива, поэтому вся структура потока вращается с Солнцем по крайне мере в течении нескольких солнечных оборотов, проходя над Землей приблизительно через каждые 27 дней, что объясняло тенденцию геомагнитных возмущений к повторению. Таким образом, структуры внутри каждого сектора вызывают возмущения в магнитосфере. Однако, Хейл обнаружил, что особенно сильные магнитные бури, не показывающие 27-дневной повторяемости. Отсутствие повторяемости объясняется тем, что вспышки – явление кратковременное и сравнительно редкое. Через несколько минут после начала вспышки магнитное поле Земли «вздрагивает», наблюдается внезапное, очень резкое и сравнительно небольшое его изменение. Эти «магнитные крючки» вызваны непостедственным действием излучения вспышки на магнитное поле Земли.

Исследования распределения международных спокойных дней (Q) и международных возмущённых дней (D) в зависимости от прохождения через центральный меридиан. (СМР) показали заметный максимум Q – дней примерно через 3 дня после СМР активных областей. Что обнаружило существования «конуса избегания» над центром активности, который достигает Земли через 2,5 – 3 дня после СМР. Таким образом, периодическая магнитная активность обусловлена М-потоками, собирающихся в пучки отклоняющим действием активных областей.

Геомагнитная активность имеет годовые пики вблизи точек равноденствий, вызванные прохождением Земли на минимально возможной гелиографической широте (7° от солнечного экватора), т.е. вектор потока солнечной плазмы по отношению Земле является важной характеристикой степени геомагнитной активности. Исходя из этого, можно ожидать зависимость геомагнитной активности от всемирного времени, учитывая, что воздействие Солнца на Землю переносится СВ с запаздыванием на 4-5 суток.[7]

3. Магнитное поле Земли

Из-за идеальной проводимости плазмы солнечного ветра магнитные силовые линии земного диполя не могут проникнуть в натекающий солнечный ветер и образует в первом приближении пустую магнитную полость около Земли – магнитосферу. В этом же приближении формы магнитосферы определяются балансом динамичного давления солнечного ветра и давлением магнитного поля Земли.

Магнитосфера представляет собой «тупое» препятствие для сверхзвукового СВ, и перед ней на расстоянии 13-17Rз от центра Земли образуется отошедшая бесстолкновительная ударная волна (на рис. 1 показана ближайшей к Солнцу поверхностью), отклоняющая поток солнечной плазмы — обтекает магнитосферу. Передача энергии и импульса СВ в магнитосфере происходит лишь благодаря диссипативным процессам, а в отсутствие последних плазма и поля внутри магнитосферы находятся в статич. равновесии.

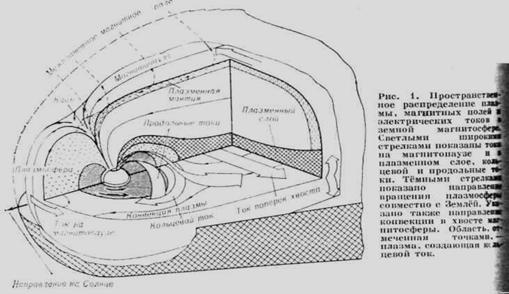
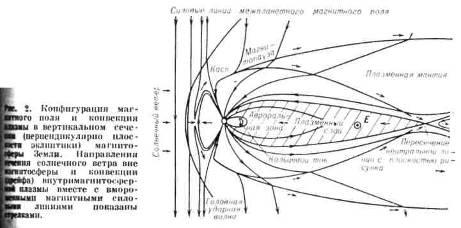
Несмотря на то, что плотность энергии межпланетного магн. поля (магнитное поле, вмороженное в плазму СВ) составляет всего 1% от плотности кинетической энергии СВ на орбите Земли, процессы пересоединения межпланетных и земных магнитных силовых линий существенно определяют структуру и динамику магнитосферы. Пересоединение происходит в небольшой области магнитосферы, где благодаря развитию плазменных неустойчивостей возрастает сопротивление плазмы, что нарушает вмороженность магнитных силовых линий в плазму. Это позволяет межпланетным и земным силовым линиям «разорваться» и «пересоединиться» между собой (см. рис.9). Наиболее благоприятной для протекания этих процессов является ситуация, когда межпланетное магнитное поле (ММП) антипараллельно земному магнитному полю в подсолнечной точке магнитопаузы. СВ увлекает пересоединённые силовые линии магнитного поля Земли, которые за тем образуют протяжённый магнитный шлейф – хвост магнитосферы.

3.1 Магнитосферные бури и суббури

Ударная волна и облако плазмы движутся со скоростью @1500 км/с и достигают Земли за 1,5-2 суток. Длительность возникающей бури пропорциональна ширине корпускулярного потока у Земли и скорости орбитального движения Земли. Для бури продолжительностью 24 часа она составит около 13°, а для двухчасовой - @ 1° (угловая широта, равная линейной, деленной на расстояние Земля –Солнце). Средний угол раствора корпускулярных потоков около 8—9°.

Типичная магнитная буря состоит из трёх фаз. Она начинается, когда межпланетная ударная волна достигает магнитосферы и сжимает её. Т.к. переходный ударный фронт имеет небольшую толщину (несколько тысяч километров), сжатие происходит весьма быстро( минуты), и отчётливо проявляется в вариациях геомагнитного поля как резкое увеличение его напряжённости.

После сжатия магнитосферы ударной волной и до начала главной фазы бури наблюдается несколько относительно спокойных часов – начальная фаза. В этот спокойный период магнитосфера окружена СВ, поток которого ослаблен в результате форшбуш-эффекта. Продолжительность периода варьирует от 10 мин. до 6 и более часов.

Главная фаза магнитосферной бури начинается, когда магнитосферы достигает плазменное облако, породившее ударную волну. Она характеризуется последовательностью взрывоподобных процессов – магнитными суббурями.

Плазменное облако турбулентно, в частности, северо-южная компонента ММП В в потоке плазмы крайне и иррегулярна. В период, когда Земля окружена потоком, в котором поле ММП В антипаралельно земному, происходит пересоединение межпланетных и геомагнитных линий, что приводит к появлению электрического поля Е, направленного поперёк магнитного хвоста с утренней стороны на вечернюю. Таким образом, при прохождении турбулентного потока плазмы наблюдается появления многих суббурь. Турбулентный М-поток также может быть причиной магнитосферных суббурь. Электрическое поле Е обуславливает внезапное начало интенсивного направления к Земле движения плазмы в магнитном хвосте и плазмосфере. В хвосте это движение обладает компонентой, направленной к нейтральному слою, т.е. происходит сложное перераспределение плазмы.

В начальной стадии развития суббури плазменный слой становится очень тонким. Вследствие этого резко меняется направление части тока, текущего в хвосте магнитосферы. Ток из хвоста магнитосферы вытекает вдоль магнитных силовых линий в утренний сектор овала полярных сияний, течёт вдоль полуночного сектора овала и вдоль силовых линий вытекает из вечерней части овала в хвост магнитосферы.

Конвекция магнитосферной плазмы к Земле и токи вдоль силовых линий приводят к ускорению частиц плазмы. Возникает горячая плазма с температурой 107 К или более; часть этой плазмы вторгается в верхнюю атмосферу высоких широт, а другая часть заполняет плазменный слой.

Горячая плазма частично инжектируется в область захвата и образует во время бури протонный пояс (так называемый кольцевой ток) и внешний радиационный пояс (электронный). Последовательное проявление магнитосферных суббурь может привести к генерации очень интенсивного протонного пояса. Его магнитный эффект на поверхности Земли проявляется в виде уменьшения горизонтальной составляющей геомагнитного поля в низких и средних широтах.

Горячая плазма, инжектируемая в высокоширотные районы, заметно возмущает полярную ионосферу, приводя к появлению полярных суббурь. Полярная электроструя, интенсивный концентрированный электрический ток вдоль овала полярных сияний, может быть идентифицирована с ионосферной частью тока, текущего из хвоста магнитосферы. Полярная электроструя вызывает полярные магнитные суббури. Для оценки активности магнитосферных суббурь используют интенсивность полярных магнитных суббурь. Для этой цели применяются индексы АЕ, AU, AL, выводимые из вариаций горизонтальной компоненты магнитного поля на станциях, расположенных в зонах полярных сияний.

В период главной фазы бури нейтральный состав верхней атмосферы в полярной области и ионосфера в средних широтах оказываются сильно возмущёнными. Причина этого явления до сих пор окончательно не установлена. Часть протонов не протонного пояса проникает в плазмосферу и возбуждает ионно-циклотронную неустойчивость. Предполагается, что в результате образуются горячие электроды. Опускаясь на высоты ионосферы в средних широтах, они приводят к образованию среднеширотных красных дуг.[8]

3.2 Единицы напряжённости магнитного поля

Их наиболее просто можно получить в рамках представлений о магнитных полюсах. Полюса одного знака испытывают отталкивание, противоположного – притяжение. И хотя магнитные полюса являются только теоретической абстракцией, они бывают полезны для описаний взаимодействия магнитных полей и магнитов. Полюсу приписывается единичная «магнитная масса», если со стороны равного ему по величине другого полюса, расположенного на единичном расстоянии, на него действует единичная сила. В системе СГС единицами силы служат дина и сантиметр. Магнитная масса полюса равна m, если на расстоянии 1 см сила, действующая на единичную массу, будет равна m дин. На расстоянии r на единичную массу действует в этом случае сила m/ r2 дин, в на массу m1 — m1· m / r2 дин (закон Кулона).

В некотором магнитном поле в точке Р на магнитную массу m1 действует пропорционаольная ей сила, если присутствие этой массы не вызывает изменений магнитных свойств тела, создающего это поле. Такое условие выполняется, если m1 мала. Если механическую силу, действующую на магнитную массу в точке Р, разделить на m1, то получится величина, называемая напряженностью магнитного поля в этой точке. В системе СГС единица напряженности называется гаусс (Гс). Физическая размерность напряженности г1/2 /см1/2·с = дин1/2 /см. В земном магнетизме часто употребляется меньшая единица напряженности поля, гамма g: 1g = 10-5 Гс. []

3.3 Составляющие магнитного поля

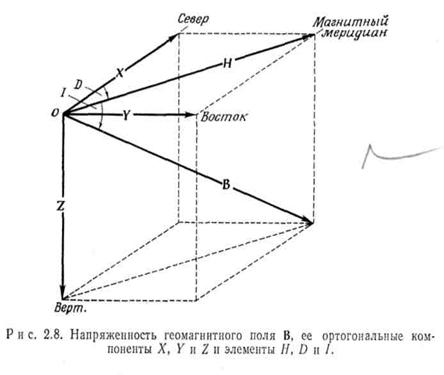
В любой точке О вектор напряженности магнитного поля F (В), может быть разложен на составляющие различными способами

В одном случае этими составляющими будут F, или В, - абсолютная величина (модуль) вектора – и два угла D и I. Угол D образован направлением на север и горизонтальной составляющей Н вектора В, I есть угол между В и Н. D считается положительным, если Н отклоняется к востоку, I положительно при отклонении В вниз от горизонтальной плоскости. Величина D называется магнитным склонением и – наклонением. Вертикальная плоскость, проходящая через Н, называется (местной) плоскостью меридиана.

В другом случае для разложения F (В) используются величины X, Y, Z - северная (Х) и восточная (Y) компоненты Н и вертикальная составляющая Z, которая считается положительной, если В направлена вниз. Напряженность F (В), называемая «полной силой», Н, Z (горизонтальная и вертикальная составляющая) и X, Y измеряются в гауссах или гаммах; D и I измеряются в дуговых градусах и минутах. Все 7 величин В, Н, D, I, X, Y, Z называются магнитными элементами. Между собой они связаны следующими соотношениями:

Н = В cos I,Z = B sin I = H tg I,

X = H cos D,Y = H sin D,(1)

X2 + Y2 = H2 ,X2 + Y2 + Z2 = H2 + Z2 = B2.

Для полного описания В достаточно трех независимых элементов. Если эти элементы заданы, то любые другие могут быть получены из соотношения (1).

Обычная стрелка компаса уравновешивается, вращаясь горизонтально на вертикальной оси. Компасная стрелка, уравновешенная до намагничиванию и способная вращаться в плоскости магнитного меридиана вокруг горизонтальной оси, называется буссолью наклонения, или инклинатором. В северной полусфере Земли почти везде северный полюс магнитной стрелки направлен вниз (I положительно), в южном полушарии вниз направлен южный полюс стрелки (I отрицательно). Области положительного и отрицательного I разделены линией (называемой магнитным экватором, или экватором наклонения), вдоль которой I= 0. Магнитная стрелка (уравновешенная до намагничивания) в любой точке на этой кривой располагается горизонтально.

В точках, где горизонтальная компонента В исчезает, магнитная стрелка устанавливается вертикально. Эти точки называются полюсами магнитного наклонения, или полюсами наклонения. Две основные точки такого типа обычно называются магнитными полюсами Земли. Одна из них находится в Арктике, вторая – в Антарктиде. На эпоху 1965г. их координаты были соответственно 75°,6 с.ш., 101° з.д. и 66°,3 ю.ш., 141° в.д.

В любой точке Р на сферической поверхности имеется естественное направление, характеризующее эту точку, — радиальное направление. Поскольку Н, Z и I определяются относительно этого направления, а В вообще не требует для своего определения какого-либо направления, эти четыре составляющие можно назвать собственными магнитными элементами. Но В не может быть определено полностью только этими элементами. Чтобы определить азимут Н, нужно выбрать некоторое нулевое направление, от которого можно отсчитать магнитное склонение D. В качестве такого направления выбрано направление на северный географический полюс. Так как ось вращения Земли не связана непосредственно с конфигурацией геомагнитного поля, D (как и X, Y) определяется относительно условного направления, принятого на основе простого соглашения. Поэтому D, X и Y можно назвать относительными магнитными элементами.

4. Индексы, характеризующие геомагнитные вариации

1) Локальный К-индекс – квазилогарифмический индекс (увеличивается на 1 при увеличении возмущённости ≈ в 2 раза), вычисляемый по данным конкретной обсерватории за 3-х часовой интервал времени. Таким образом, мы имеем 8 К-индексов для каждых гринвичских суток. Для одного интервала используются магнитограммы для трёх компонентов (, D —магнитное склонение, т.е. угол между плоскостями гринвичского и магнитного меридианов; Н —магнитный меридиан, азимут которого определяется по D; Z —показатель напряженности магнитного поля по вертикали, см. рис.10) на каждой станции. Для каждой компоненты оценивается амплитуда r в течении интервала учитывается поправка на вариации солнечно-суточные (Sq), лунно-суточные (L), а когда необходимо, вариации радиационного излучения (Sqа). (Sqа исключаются, т.к. они обусловлены рентгеновским и ультрафиолетовыми излучениями из областей солнечных вспышек, а не потоком солнечной плазмы.)

Наибольшая из трёх амплитуд в каждом временном интервале. используется для К-индекса. Для каждой обсерватории имеется таблица, дающая пределы r, определяемое полулогафмической шкалой, для каждой из 10 величин К. Например, таблица.1 для обсерваторий на широте 50°.

Таблица 1.

r(g)	0 ô 5ô 10ô 20ô 40ô 70 ô 120 ô 200ô 300 ô >500ô
K	0 1 2 3 4 5 6 7 8 9

2) Трёхчасовой планетарный Кр- индекс, введенный Бартельсом в 1939г., усреднённые К–индексы для 12 выбранных обсерваторий, расположенных в северном и южном полушариях, от умеренных широт вплоть до 63°(изменяется от 0 до9).

Таблица 2.

Обсерватория	Широта	Обсерватория	Широта
Минук (Канада)	61,8°N	Руде Сков (Дания)	55,9°N
Ситка (Аляска)	60,0	Вингст (Ирландия)	51,6
Лервик (Шотландия)	62,5	Виттевин (Голландия)	54,1
Эксдалемьюр (Шотландия)	58,5	Хартланд (Англия)	54,6
Лёво (Швеция)	58,1	Ажинкоурт (Канада)	55,1
Фредериксбург (США)	49,6	Амберлей (Новая Зеландия)	47,7°S

Кр – индекс отражает флуктуации электрического тока, не учитывая структуру поля возмущения. Интерпретация связи между Кр – индексом и другими геомагнитными данными не всегда прямая. Одна из причин заключается в том, что 12 станций, участвующих в определении Кр – индекса, расположены в субавроральной зоне. Это указывает на то, что большие значения Кр, как 6, 7, 8, 9, обусловленные главным образом полярными магнитными возмущениями. С другой стороны, низкие значения Кр могут быть следствиями других типов геомагнитных возмущений.

Количественно состояние магнитного поля в зависимости от Кр можно приблизительно охарактеризовать данным образом

Таблица 3.

Кр £= 2 и менее	спокойное
Кр = 2 …3	слабо возмущенное
Кр = 4	возмущенное
Кр = 5 …6	магнитная буря
Кр ³= 7 и более	большая магнитная буря

Кр - индекс обладает полулогарифмической связью с амплитудой r. Для того, чтобы Кр перевести в линейную шкалу Бартельс ввел следующую таблицу для получения трехчасового ар – индекса, измеряющего изменчивость индукции (индуктивность) геомагнитного поля в нанотесла (нТл),

Таблица 4.

Кр	= 00 0+ 1- 10 1+ 2- 20 2+ 3- 30 3 4- 40 4+
ар	= 0 2 3 4 5 6 7 9 12 15 18 22 27 32
Кр	= 5- 50 5+ 6- 60 6+ 7- 70 7+ 8- 80 8+ 9- 90
ар	= 39 48 56 67 80 94 111 132 154 179 207 236 300 400

Эта таблица составлена таким образом, что ар – индекс станций на геомагнитной широте ~ 50° может рассматриваться как амплитуда наиболее возмущенной из трех компонентов поля, выражаемая в единицах 2g. Ежедневный Ар –индекс получается в результате суммирования восьми величин ар для каждого дня. Именно он использован в данной работе.

5. Постановка задачи

Цель работы:

Статистический анализ Ар и Rw- индексов, описывающих солнечную и геомагнитную активности, c помощью их автокорреляционных и взаимокорреляционной функций.

Вычитая из функции Х(t) ее среднее значение по 365 точкам, приводим исходную реализацию к виду Y(t), близкой к стационарному в смысле математического ожидания. Очевидно, что это ожидание центрирует реализацию, т.е. my(t) = 0.

Систематика оценок: оценки характеристик случайных функций обознацим символом «тильда», K(t) – оценка приближенного значения корреляционной функции, полученного по реализации конечной длины.

Оценка параметра несмещённая, если при увеличении объема выработки и ее реализации математическое ожидание оценки стремится к истинному значению параметра, т.е. оценка не имеет систематической ошибки, оценка параметра состоятельна, если при увеличении длины реализации дисперсия оценки стремится к нулю. Несмещенная оценка является эффективной, если она обладает свойством минимума дисперсии по сравнению с другими оценками. В предположении эргодичности изучаемого процесса в качестве оценки корреляционной функции можно принять следующее выражение:

где (1)

Из-за конечности реализации, что предполагает y(t) = 0 при t < 0 и t > T, при вычислении Kх(t) при конкретном t верхний предел интеграла и нормированный множитель превращаются T-t, т.е.

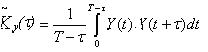(2)

При равномерном дискретном задании реализации интервал между отдельными t равен T/n, n—общее число измеренных значений. Тогда t = m·∆t = m·T /n, T-t =( n – m) T /n, а выражение (2) превращается в

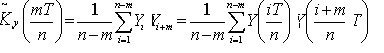(3)

Эта оценка корреляционной функции является несмещенной, но, к сожалению, несостоятельной. Последнее утверждение чего понять, если учесть, что при m → n в формировании оценки принимает участие всего несколько сомножителей, из-за чего дисперсия оценки (3) не будет стремиться при больших m к нулю каким бы большим не было число n. По этой причине подобная оценка обычно используется при m £ n /5/

Чтобы получить состоятельную оценку корреляционной функции, приходится вводить весовую функцию, которую часто называют окном данных. Смысл подобного преобразования заключается в уменьшении веса значений корреляционной функции при больших m пропорционально числу точек, принимающих участие в формировании этих значений.

Простейший вид весовой функции – это «треугольник»

Λ(m) =, которая обеспечивает линейное уменьшение веса.

В этом случае оценка корреляционной функции запишется как

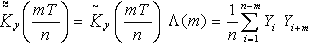(4)

Оценка вида (4), часто называемая усеченной оценкой, будет состоятельной, но смещенной, со смещением (n-m)/n .

При получении оценок взаимных корреляционных функций двух случайных процессов, X(t) и Y(t), к стационарному в указанном выше смысле виду, следует учесть, что функция Kxy(t) не является четной функцией, поэтому она должна быть получена в интервале – T … + T.

На практике используют соотношение Kxy(t) = Kxy(-t), т.е. учитывают зеркальную симметрию взаимной корреляционной функции. Несмещенные оценки находят на интервале 0…-Т с помощью выражений

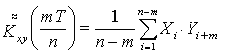(5)

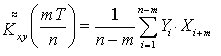(6)

Если ввести весовую функцию в треугольник, то выражение (5) и (6) перепишутся в виде

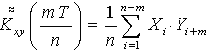(7)

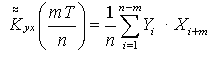(8)

Чтобы из этих выражений сформировать, например взаимную корреляцию функции Kxy(t) на интервале – T … + T, необходимо отразить выражение (8), полученное на интервале 0 … -Т относительно оси координат в положение 0…-Т, а выражение (7) оставить без изменений.

6. Реализация задачи

Для прослеживания внутригодовых вариаций изменчивости чисел Вольфа и Ар-индекса был взят год максимума солнечной активности 2002 год за прошедший цикл (1997г.-2008г). В приложении (таблица 5) находятся исходные данные к построенным диаграммам №1- №3.

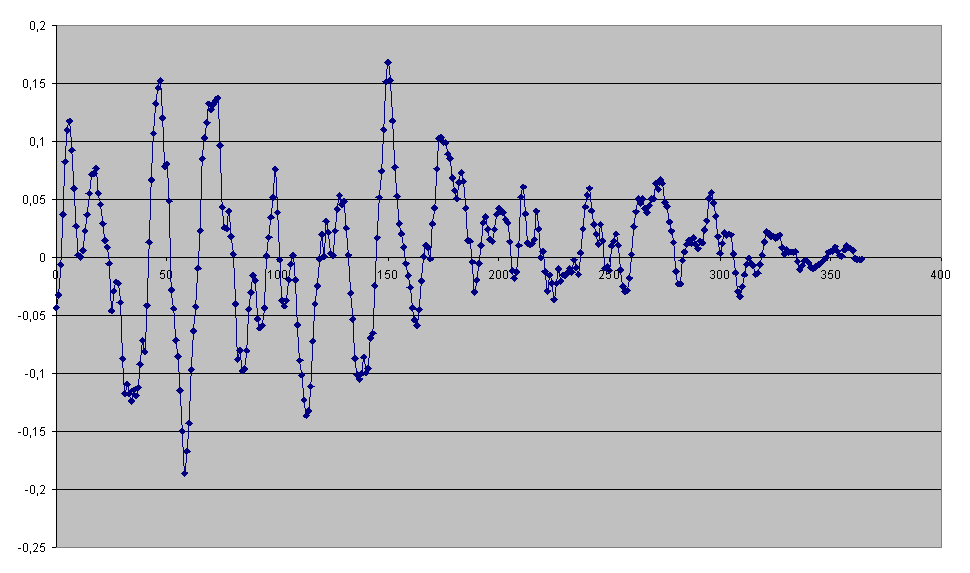
Автокорреляционная функция Ар показывает полугодовые пики, связанные с достижением Землей в ее годичном движении наибольших гелиоцентричный широт в , которые сопровождаются постепенно затухающими всплесками. Как и ожидалось, проявляется 25-27 дневная цикличность.

Как видно из диаграммы №3, четкая цикличность Ар индекса не полностью совпадает с внутригодовыми циклами показателя солнечной активности, т.к. изменчивость индексов Ар больше чем чисел Вольфа.

Между тремя наибольшими положительными пиками в точках 19, 104, 195 имеется периодичность около 90 дней (диаграмма №2). Подобное наблюдается с тремя наибольшими отрицательными пиками в точках 47, 133, 236 (период между ними так же около 90 дней). Исходя из данных фактов следует предположение, что данная периодичность является внутригодовым циклом чисел Вольфа.

Из взаимной корреляционной функции Ар и Rw видна наибольшая взаимосвязь с 27 дневной цикличностью. Исходя из подобного разброса, можно сделать вывод, что некая взаимосвязь между числами Вольфа и Ар-индексом существует, но довольно слабая.

Выводы

Основной задачей настоящей работы являются статистические оценки автокорреляционных функций Ар и Rw и связи между изменениями солнечной активности и предполагаемыми результатами их воздействий – проявлениями природных процессов на Земле.

Для того, чтобы более детально отобразить характер солнечно-земных связей был рассмотрен год максимума прошедшего цикла, т.е. 2002 год. Как и ожидалось, автокорреляционная функция Ар-индекса выявила 25-27 дневную цикличностью со смещением в 2-5 дня, а также полугодовые пики , связанные с достижением Землей наибольших гелиографичных широт. Автокорреляционная функция чисел Вольфа за данный год показала, что между положительными и отрицательными пиками имеется цикличность примерно равная 90 дням.

Изменчивость процессов, происходящих в биосфере, бесспорно, связана с солнечной активностью. В наше время существуют предположение, что солнечная активность (её минимумы) влияет на физиологию, психологию людей, а как следствие, на все факторы, связанные с человеческой деятельностью.

Литература

1. http/www/krugosvet.ru/articles/125/1012579/10125/a4.htm Гелиофизические связи

2. С.-И. Акасофу, C. Чепмен. Развитие центра активности. Солнечно-земная физика. 2-я часть. М.: «Мир» — 1974. —с. 194-197.

3. И.П. Дружинин, Н.В. Хомянова. Выбор характеристик солнечной активности.// Солнечная активность и переломы хода природных процессов на Земле. М.: «Наука» - 1969г. – с.13.

4. В.П Вязыцин. Природа пятен //Курс астрофизики и звездной астрономии том №3 М.: «Мир» — 1964. — с. 61-62.

5. В.П Вязыцин. Магнитное поле пятен. Общее магнитное поле Солнца..//Курс астрофизики и звездной астрономии том №3 М.: «Мир» — 1964. — с. 57.

6. Бакулин П.И., Канонович Э.В., Мороз В.И. Общие сведения о Солнце.// Курс общей астрономии. 5-е изд. М.: «Наука» 1983 — с.265.

7. С.-И. Акасофу, C. Чепмен. М-потоки; межпланетная секторная структура и разрывы. Солнечно-земная физика. 2-я часть. М.: «Мир» — 1974. —с.280-293.

8. С.-И. Акасофу, C. Чепмен. Магнитосферные бури.// Солнечно-земная физика. 2-я часть. М.: «Мир» — 1974. —с.319-322.

9. С.-И. Акасофу, C. Чепмен. Солнце и межпланетные магнитные поля. Солнце как источник межпланетной секторной структуры. // Солнечно-земная физика. 2-я часть. М.: «Мир» — 1974. —с.13.

10. С.-И. Акасофу, C. Чепмен. Магнитное поле Земли. Составляющие магнитного поля. // Солнечно-земная физика. 2-я часть. М.: «Мир» — 1974. —с. 96-99.

11. С.-И. Акасофу, C. Чепмен. Геомагнитные индексы. // Солнечно-земная физика. 2-я часть. М.: «Мир» — 1974. —с. 293-301.

12. А.М. Грецкий,Н.Н. Евсюков. Корреляционный анализ солнечно-земных связей.//Астрофизические приложения методов теории случайных функций. Харьков ХГУ 1988 —с.10-14.

13. И.П. Дружинин, Н.В. Хомянова.. Солнечная активность и переломы хода природных процессов на Земле. М.: «Наука» - 1969г. – с.323.

ПРИЛОЖЕНИЯ

Таблица 5

			Автокорреляционная функция		Взаимнокорреляционная функция
Ар	Rw	m	Ар	Rw	Ap и Rw
8	136	0	1	1	-0,043418337
8	135	1	0,479214	0,891484405	-0,032346353
2	136	2	0,2362601	0,75712881	-0,006358507
3	142	3	0,2212125	0,603324564	0,037205603
2	118	4	0,0964894	0,457647913	0,082522988
2	98	5	0,0393132	0,32324094	0,10987131
7	90	6	0,0656402	0,207290476	0,117568707
11	100	7	0,0039018	0,109998494	0,092385046
2	121	8	-0,0375195	0,048297058	0,059495084
19	115	9	-0,0351303	0,004253873	0,02682969
27	129	10	-0,0524914	-0,010780692	0,001864774
17	129	11	-0,0636552	-0,024308911	0,000603082
13	124	12	-0,0180339	-0,023297191	0,006025588
8	122	13	-0,0913351	-0,015678333	0,022763809
7	104	14	-0,1147042	0,011263122	0,036970394
4	87	15	-0,0900614	0,045129909	0,055126233
8	74	16	-0,0203419	0,089272458	0,071638867
5	86	17	0,0410715	0,128538273	0,07249978
14	99	18	0,0474759	0,15623411	0,076967666
10	109	19	0,0540686	0,162322499	0,05540944
11	118	20	0,0754446	0,159601194	0,045723299
6	120	21	0,0996992	0,150926147	0,029195898
8	140	22	0,0857559	0,138651926	0,014629419
4	115	23	0,1812762	0,109614039	0,008907192
10	94	24	0,2494436	0,076498445	-0,005239299
8	106	25	0,1530436	0,047347525	-0,045942437
8	118	26	0,1761347	0,035047614	-0,029064068
7	121	27	0,217776	0,031960456	-0,021164192
4	116	28	0,0884773	0,030478354	-0,022349424
3	119	29	0,0744265	0,020734717	-0,038802115
6	112	30	0,12363	0,003535305	-0,087335761
14	113	31	0,0044973	-0,012855953	-0,11738497
19	135	32	-0,0335014	-0,028683285	-0,109299685
4	159	33	0,0684985	-0,047862021	-0,117414507
6	153	34	0,0085433	-0,068890926	-0,123895245
23	151	35	-0,0375829	-0,084925279	-0,114150682
22	125	36	-0,0100632	-0,100522647	-0,119140025
15	104	37	-0,063348	-0,096154562	-0,112206678
11	104	38	-0,0781112	-0,093039943	-0,092163737
11	110	39	-0,0682877	-0,087322278	-0,071548518
9	105	40	-0,0587905	-0,099526075	-0,081282005
14	109	41	-0,0576537	-0,118081799	-0,041537316
9	110	42	-0,0270442	-0,135020862	0,012954569
12	104	43	0,0084534	-0,166505443	0,066783526
3	92	44	0,0557459	-0,193146244	0,106890041
3	103	45	0,0447363	-0,220788931	0,132614053
5	79	46	0,0548359	-0,239884132	0,146020753
12	91	47	0,0805798	-0,251149379	0,152486723
11	80	48	0,0847666	-0,234010116	0,120250916
6	78	49	0,0630902	-0,201826605	0,07819627
8	95	50	0,1209761	-0,166331819	0,080623072
8	81	51	0,0990873	-0,129527758	0,04863746
8	84	52	0,0145549	-0,092981477	-0,028102599
4	94	53	0,0113397	-0,060652334	-0,044156542
5	99	54	0,0024735	-0,031708788	-0,071434715
6	121	55	-0,0608464	-0,003848406	-0,085279907
8	123	56	-0,0541288	0,021702056	-0,114540308
6	107	57	-0,0414586	0,024324856	-0,149752173
25	97	58	-0,0696189	0,020426976	-0,186051037
10	109	59	-0,0389993	0,022246583	-0,167098137
6	78	60	0,0656977	0,008545165	-0,142760838
11	112	61	-0,0219932	-0,00733864	-0,096748902
10	114	62	-0,0935731	-0,041139369	-0,063192189
21	106	63	-0,0614018	-0,067154588	-0,042466642
17	112	64	-0,0125294	-0,090177788	-0,009331003
9	93	65	-0,0375005	-0,100496957	0,023005533
4	79	66	-0,0014797	-0,105168	0,085112459
5	74	67	-0,0187064	-0,111633758	0,103032872
9	78	68	-0,0718499	-0,119338808	0,116183732
10	103	69	-0,0677408	-0,132155164	0,132387748
11	90	70	-0,0290101	-0,139219751	0,127473985
5	92	71	0,0217804	-0,134610717	0,13211084
3	87	72	0,0257696	-0,130858292	0,135095584
5	100	73	0,0192042	-0,128915641	0,137508921
3	94	74	0,0172377	-0,125149043	0,096499576
2	88	75	0,0019482	-0,113245989	0,043337328
14	92	76	-0,0085841	-0,099870667	0,025763105
19	76	77	0,0111599	-0,078285542	0,024869614
9	85	78	0,0218238	-0,047810908	0,039937981
7	95	79	0,0147391	-0,008286029	0,018103042
6	93	80	0,0176358	0,030317929	0,002735658
13	106	81	-0,011677	0,066952439	-0,040115854
45	111	82	-0,0526823	0,091704093	-0,087744933
7	109	83	0,0336655	0,107460558	-0,080271018
11	101	84	0,0627905	0,115806072	-0,097679314
4	115	85	-0,0497856	0,109428012	-0,096211809
2	107	86	-0,0651392	0,086566567	-0,080303161
5	114	87	-0,0385303	0,070373028	-0,044545734
20	111	88	-0,0388218	0,045501785	-0,030106111
20	125	89	-0,0523814	0,016975028	-0,015378244
18	116	90	-0,0177286	-0,003703376	-0,019953549
14	130	91	-0,0324916	-0,01375774	-0,052840166
14	126	92	-0,0275614	-0,019941712	-0,060901995
5	127	93	0,0011895	-0,017907731	-0,058831374
3	127	94	0,0241376	-0,007747783	-0,04355538
4	136	95	0,0241313	0,01184636	0,001208944
7	138	96	0,0043356	0,013464792	0,017315645
2	134	97	-0,0193706	0,015457404	0,034599191
3	148	98	-0,0214708	0,029523417	0,051956449
5	142	99	-0,0018771	0,051929806	0,076098935
15	152	100	-0,0142455	0,088650598	0,038783871
16	162	101	-0,0376194	0,122096433	-0,002087532
17	144	102	-0,0738232	0,142632013	-0,037045322
13	150	103	-0,0545084	0,162310984	-0,041888284
6	138	104	0,0248139	0,161644831	-0,036964747
7	113	105	-0,0424543	0,150911974	-0,019140264
62	94	106	-0,0218078	0,12259339	-0,005778694
63	106	107	0,056215	0,088849912	0,001749819
62	104	108	-0,0318495	0,057137403	-0,019424383
70	102	109	-0,0935358	0,039717948	-0,058198503
5	95	110	0,0010615	0,02451044	-0,08873203
11	93	111	0,0221797	0,018165422	-0,101385106
27	114	112	-0,0430894	0,013809296	-0,122796299
7	150	113	-0,0428667	0,003870924	-0,136255993
3	147	114	-0,0544136	-0,013758803	-0,132356256
3	101	115	-0,0437658	-0,026875371	-0,111233047
10	88	116	-0,0191289	-0,03483448	-0,072086263
20	71	117	-0,0276266	-0,033693959	-0,040042881
9	87	118	-0,0380482	-0,015874901	-0,024506919
7	85	119	0,0141197	0,009950393	-0,001317955
4	102	120	0,02684	0,041080372	0,019788642
5	114	121	0,0233023	0,077495903	0,000974991
5	149	122	0,0363263	0,09614216	0,031285849
4	166	123	0,0626462	0,101572369	0,021754125
3	172	124	0,021443	0,094654832	0,003125609
8	149	125	-0,0452167	0,066488613	0,001710189
8	157	126	-0,0687121	0,034504062	0,022846773
8	142	127	-0,0653697	0,005782552	0,041557949
6	126	128	-0,0558907	-0,024367996	0,053492583
15	133	129	-0,0753275	-0,050213665	0,045497212
49	138	130	-0,023204	-0,074709488	0,048391826
15	130	131	0,0331099	-0,093543986	0,025367832
8	104	132	-0,0013426	-0,103240409	0,001995983
29	76	133	-0,0224513	-0,103261669	-0,030834108
12	74	134	0,0022782	-0,094203053	-0,053132277
7	84	135	-0,0586191	-0,080248301	-0,086838195
5	86	136	-0,0699612	-0,05816303	-0,101005253
14	93	137	0,0237704	-0,029783146	-0,10494343
11	93	138	0,0083415	0,000938142	-0,100070932
10	107	139	-0,0045553	0,037386147	-0,085886499
10	121	140	0,0550228	0,075229123	-0,099606812
8	137	141	0,0307604	0,093319869	-0,095464048
78	136	142	0,058634	0,099736019	-0,069626015
2	128	143	0,1269622	0,101964797	-0,065461968
4	127	144	0,1086436	0,093043486	-0,024429602
7	121	145	0,0390211	0,066468681	0,016906625
22	123	146	0,036576	0,035110597	0,051793562
9	119	147	0,0114217	0,000240565	0,074391877
7	114	148	-0,0043813	-0,039380442	0,110156689
6	103	149	0,0161049	-0,073966267	0,151432517
3	120	150	-0,0086075	-0,090682718	0,168137357
4	124	151	-0,0600387	-0,085409657	0,152793168
16	129	152	-0,0800478	-0,082960128	0,117816078
10	133	153	-0,0738563	-0,075546963	0,07775756
13	150	154	0,0026852	-0,06274478	0,052886209
6	126	155	-0,0227987	-0,048118738	0,029014333
4	135	156	-0,0469697	-0,027205613	0,020459672
5	135	157	-0,0502587	-0,014904019	0,008729927
14	127	158	-0,0811191	-0,003669209	-0,00532463
8	113	159	-0,079125	0,001567337	-0,015782247
14	88	160	-0,0522484	0,00900334	-0,025817835
8	68	161	-0,0214382	0,028625174	-0,043393361
6	75	162	-0,0498675	0,043401897	-0,053873088
7	55	163	-0,001672	0,046172013	-0,05878772
4	73	164	0,101091	0,049738145	-0,04496468
4	70	165	0,1033242	0,042944449	-0,020232412
7	80	166	0,1681775	0,042837528	0,000735494
4	60	167	0,2343454	0,042432875	0,01056888
10	87	168	0,1634896	0,038017309	0,008727169
11	79	169	0,0826404	0,033938009	-0,001300209
5	74	170	0,1038285	0,028229203	0,029040829
7	57	171	0,0847623	0,020166538	0,042583703
6	57	172	0,0779898	0,017296323	0,076355645
9	65	173	0,0716859	0,01084341	0,102689723
5	74	174	-0,0043393	-0,002754294	0,103662051
8	76	175	-0,0488913	-0,016183883	0,09920611
5	74	176	-0,0462658	-0,031437367	0,098992402
2	66	177	-0,0615796	-0,036613428	0,089144894
2	60	178	-0,0552991	-0,037438678	0,085297065
5	66	179	-0,0305243	-0,03437216	0,068477987
12	72	180	-0,0391724	-0,026999212	0,057631655
14	58	181	-0,0486296	-0,016321011	0,050783661
5	61	182	-0,0128944	-0,005450397	0,064450981
4	80	183	-0,0338942	0,00576589	0,07299626
5	82	184	-0,0237459	0,01302134	0,065610738
12	88	185	-0,0154427	0,019054718	0,042569152
22	75	186	-0,0339494	0,023917457	0,014862521
8	66	187	0,0195921	0,026091844	0,014032426
8	63	188	0,0710448	0,033316945	-0,003929664
12	64	189	0,0540186	0,039562129	-0,029883282
7	58	190	0,0941402	0,047839698	-0,019606816
5	61	191	0,1089652	0,05855156	-0,005164023
19	52	192	0,0372673	0,058794635	0,010335995
6	72	193	0,0166457	0,07060813	0,029944527
2	78	194	0,066014	0,078758582	0,035101752
4	96	195	0,0172031	0,094702667	0,024290605
12	99	196	0,010791	0,101946194	0,015604852
20	91	197	0,0393637	0,08897393	0,013824365
5	92	198	0,0232185	0,065556619	0,024070816
10	83	199	0,0096718	0,051877807	0,037300295
18	77	200	-0,0107769	0,03463118	0,042297022
20	77	201	-0,0594354	0,014832443	0,039769665
16	91	202	-0,0645327	-0,011868151	0,038648566
17	121	203	-0,074246	-0,019179711	0,032887138
7	129	204	-0,0812464	-0,03268224	0,029905869
12	133	205	-0,0689304	-0,031674329	0,013446684
12	164	206	-0,0410754	-0,0264794	-0,011532282
17	182	207	-0,0417905	-0,020513522	-0,017994146
11	192	208	-0,0594247	-0,016199119	-0,012634485
10	181	209	-0,0713307	-0,013415717	0,010292732
6	174	210	-0,0335097	-0,01041856	0,052055701
7	148	211	-0,0389379	-0,009201237	0,060856821
25	137	212	-0,0295624	-0,013191333	0,037631716
42	132	213	-0,040322	-0,028320267	0,012471533
14	121	214	0,0549605	-0,042550338	0,010915526
13	95	215	0,073122	-0,047543207	0,011774853
4	84	216	0,0467915	-0,046522452	0,015273648
4	87	217	0,0655843	-0,039335707	0,039927122
4	88	218	0,0839476	-0,033681735	0,024342294
6	76	219	0,0005831	-0,023849602	-0,000195763
14	73	220	-0,0332249	-0,016176973	0,005174209
15	73	221	-0,0153628	0,000604875	-0,012111009
13	99	222	-0,0245943	0,019404892	-0,02913639
12	117	223	-0,0098293	0,047011613	-0,015182583
8	134	224	-0,0181159	0,065857185	-0,022145272
12	177	225	-0,0441091	0,075725371	-0,036262378
22	185	226	-0,039035	0,067651811	-0,022315543
11	174	227	-0,0427505	0,049904418	-0,009951147
8	186	228	-0,0511994	0,022971733	-0,020305863
21	179	229	-0,0757508	-0,013448138	-0,015005058
30	164	230	-0,0707062	-0,056012295	-0,01565109
30	140	231	-0,0579844	-0,098190226	-0,013355597
32	127	232	-0,046613	-0,128177735	-0,009455166
8	114	233	-0,0357756	-0,144306253	-0,012786252
7	123	234	-0,0482159	-0,157073002	-0,002058197
4	99	235	-0,0508083	-0,162743274	-0,008873898
5	98	236	-0,042032	-0,164856006	-0,014651506
16	79	237	-0,0442165	-0,159058173	0,003921845
13	80	238	-0,02232	-0,144543659	0,024604
7	81	239	-0,0145757	-0,12315147	0,043496306
8	82	240	-0,00985	-0,104439838	0,053592053
8	97	241	-0,0238497	-0,083434762	0,059578483
7	106	242	-0,024697	-0,065208749	0,040176665
11	120	243	-0,0233243	-0,05329976	0,02852502
8	136	244	-0,0192933	-0,046015307	0,020039271
7	147	245	-0,0185415	-0,031121387	0,011336817
42	144	246	-0,037692	-0,019225154	0,028410347
7	132	247	-0,0265572	0,000531198	0,01445552
7	118	248	-0,0052209	0,008478284	-0,009311131
57	120	249	-0,0292401	0,019068183	-0,007836763
36	124	250	-0,027161	0,019650801	-0,011364421
9	116	251	-0,0084985	0,031802422	0,010016454
24	118	252	-0,0201959	0,039541134	0,014162389
26	109	253	-0,0195217	0,029752939	0,020143171
14	109	254	-0,0119997	0,021349757	0,010546337
11	109	255	-0,0342476	0,009834082	-0,010662942
8	87	256	-0,0513297	0,000542148	-0,024941502
6	97	257	-0,0534701	-0,01207597	-0,029268871
6	99	258	-0,0474275	-0,026896188	-0,028573017
11	116	259	-0,0394863	-0,04096167	-0,017831346
14	121	260	-0,0210223	-0,058832461	0,002497364
15	112	261	-0,0135992	-0,065361822	0,02661077
4	114	262	-0,0165691	-0,065661325	0,039310757
6	106	263	-0,0041214	-0,072781454	0,050559745
6	108	264	0,0121846	-0,068972335	0,047097416
2	112	265	0,009205	-0,062982451	0,05044377
2	103	266	0,0062812	-0,057382781	0,042241857
2	111	267	-0,0219313	-0,046882812	0,038862709
5	90	268	-0,0409263	-0,036995314	0,044591994
6	90	269	-0,0390833	-0,02936246	0,050495025
5	80	270	-0,0204422	-0,027628248	0,050670509
4	76	271	-0,0399021	-0,028585488	0,063642626
28	64	272	-0,0408476	-0,029036116	0,0586674
67	58	273	-0,0643431	-0,024413706	0,066881475
53	70	274	-0,0523951	-0,015918131	0,063790962
45	67	275	-0,0433397	-0,00884217	0,047463369
64	60	276	-0,028799	0,004467724	0,0440688
28	76	277	-0,0205533	0,017237769	0,030582393
15	81	278	-0,0069036	0,033973265	0,022620902
48	79	279	-0,0269719	0,043664461	0,012912088
33	101	280	-0,0348378	0,049745941	-0,011964215
20	106	281	-0,0339474	0,045702782	-0,022957102
16	129	282	-0,032648	0,04330977	-0,022888906
6	121	283	-0,0197308	0,041306705	-0,002554332
6	122	284	-0,020512	0,038933712	0,004756284
5	119	285	-0,0219801	0,032396644	0,01140725
23	114	286	-0,00772	0,030811785	0,014592476
18	116	287	0,0037648	0,027143161	0,012186415
18	128	288	-0,0029743	0,026634245	0,016973865
13	110	289	0,009056	0,021574229	0,011027071
14	118	290	-0,0076661	0,021023679	0,007419142
14	120	291	-0,0182709	0,022833099	0,013827232
10	122	292	-0,0169825	0,014226793	0,012626319
8	93	293	-0,0164551	-0,003048314	0,023672068
10	88	294	-0,0221362	-0,013903284	0,031592945
11	77	295	-0,0158594	-0,022064897	0,050751518
63	73	296	-0,0055941	-0,021801979	0,05573478
39	77	297	-0,0025389	-0,024630648	0,046881536
27	81	298	0,000308	-0,026686244	0,035571736
25	84	299	-0,0051976	-0,032597819	0,018046075
19	87	300	-0,0191277	-0,035844694	0,003662442
14	114	301	-0,0263008	-0,035616501	0,01200624
16	120	302	-0,0153011	-0,037374454	0,021260425
20	110	303	-0,0212088	-0,03751734	0,01915095
7	124	304	-0,0130932	-0,03122317	0,020463885
28	115	305	-0,0111547	-0,029137899	0,019500006
35	123	306	-0,0121729	-0,019599245	0,002971801
23	107	307	-0,0221724	-0,011125285	-0,013122017
24	122	308	-0,0178035	0,001862969	-0,029405262
21	137	309	-0,0146722	0,011963291	-0,033855557
13	145	310	-0,0150848	0,016383286	-0,025095702
5	122	311	-0,0112956	0,01480321	-0,014892275
6	129	312	-0,0026837	0,020059174	-0,006121105
17	126	313	0,0035081	0,020844384	-0,000472798
12	114	314	0,0082665	0,021373852	-0,004820331
17	100	315	0,0056806	0,02316963	-0,007087417
13	94	316	-4,31E-05	0,016378945	-0,014728693
8	104	317	0,0065953	0,00929673	-0,013629465
12	102	318	5,848E-05	0,002103351	-0,006069741
7	89	319	-0,0062003	-0,00579111	0,00204441
7	91	320	-0,0028173	-0,006988617	0,013303669
10	93	321	0,0001706	-0,019078548	0,021970657
14	74	322	-0,0050465	-0,033619372	0,020663498
25	94	323	-0,0043359	-0,047484741	0,018048616
50	82	324	0,0013451	-0,059982549	0,018376997
26	79	325	0,0044386	-0,068062664	0,016896765
17	77	326	-0,0054047	-0,071427179	0,01776124
15	67	327	-0,0070953	-0,069659394	0,019243448
15	56	328	-0,0010882	-0,06722767	0,00835116
13	49	329	-0,000471	-0,061741476	0,002811715
24	68	330	-0,0012286	-0,053917546	0,006890193
12	70	331	-0,0051929	-0,051431874	0,004559342
14	61	332	-0,0088191	-0,046989202	0,004799438
16	61	333	-0,0061379	-0,044251862	0,004516166
18	72	334	-0,000827	-0,044485725	0,00483106
13	66	335	-0,0019963	-0,045380425	-0,003368181
11	64	336	0,0002286	-0,041214755	-0,010549898
12	80	337	-0,0027406	-0,031884274	-0,007147859
9	82	338	-0,0005492	-0,020555511	-0,002946564
9	82	339	-0,0047573	-0,008299556	-0,00259425
18	79	340	-0,0003674	-0,004311134	-0,004443432
12	98	341	0,0036426	-0,006444179	-0,008601095
6	107	342	0,0109473	-0,005696511	-0,009552312
5	94	343	0,0090491	-0,001359829	-0,008407519
4	74	344	0,0043624	0,001227582	-0,006689168
5	65	345	0,0018635	0,003235164	-0,005806754
4	75	346	0,0036543	0,005176655	-0,003887465
13	124	347	0,0042451	0,0059851	-0,002248408
8	119	348	-0,0009587	-0,001033777	-3,30869E-05
5	129	349	0,000175	-0,008019267	0,004631664
3	140	350	0,0034437	-0,012879428	0,005502546
3	134	351	-0,0013197	-0,014681673	0,00540414
25	134	352	-0,0111238	-0,013590582	0,009160471
21	124	353	-0,0075515	-0,015615173	0,005407224
21	112	354	-0,0090024	-0,017407939	0,001686469
10	104	355	-0,0082947	-0,019915579	0,000981504
24	75	356	-0,0067102	-0,024721359	0,006272394
20	57	357	-0,00624	-0,025655478	0,009993367
12	35	358	-0,0050479	-0,029505523	0,008575337
15	32	359	-0,001991	-0,033039677	0,007694378
37	29	360	-0,0011758	-0,034476955	0,00604559
19	27	361	0,0010245	-0,030861481	-0,00084647
13	31	362	0,0014704	-0,021783376	-0,002016537
11	29	363	0,0007777	-0,014456758	-0,001967605
7	33	364	0,0005798	-0,007137491	-0,001501542

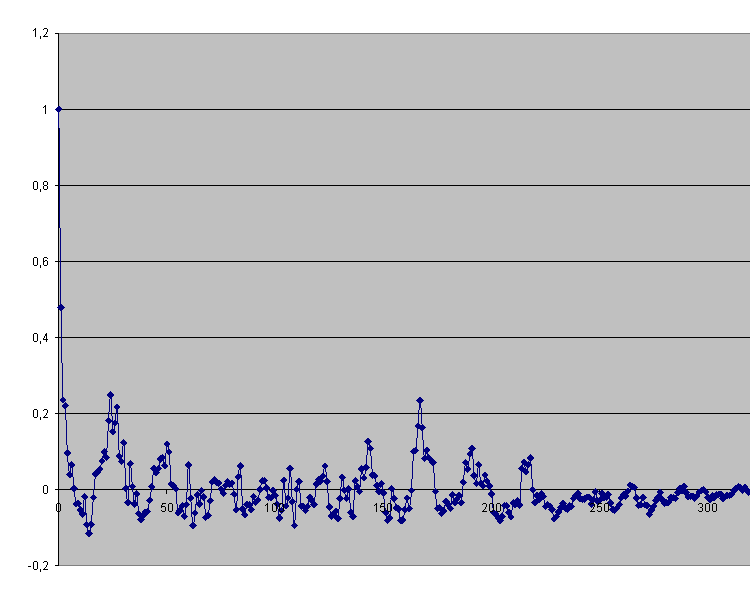Подпись: Диаграмма №1 Автокорреляционная функция Ар-индекса за 2002 год

Диаграмма №2 Автокорреляционная функция Rw за 2002 год

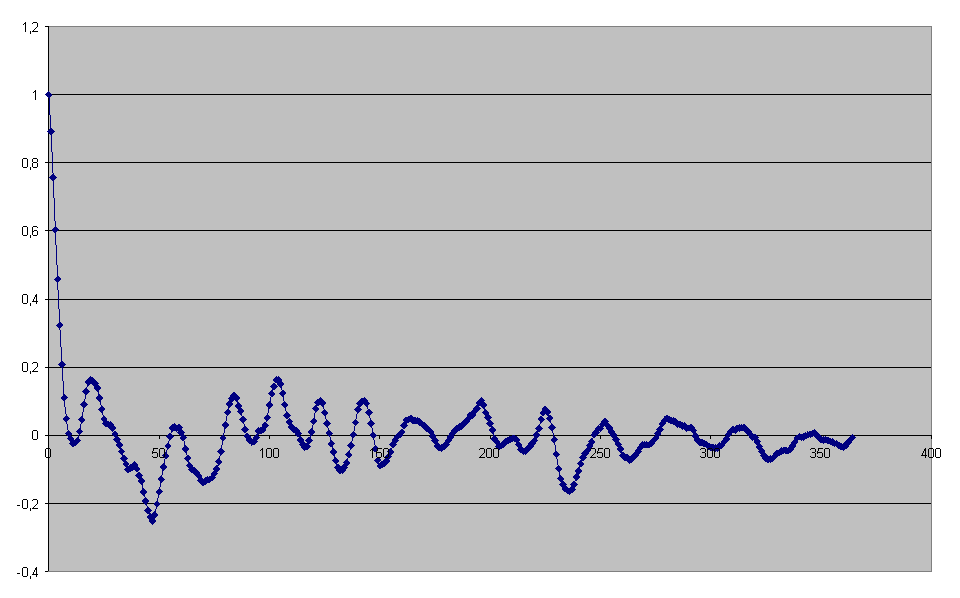
Диаграмма №3 Взаимнокорреляционная функция Ар и Rw за 2002 год