Контрольная работа: Расчет параметров электрических схем

1. Расчет линейной цепи постоянного тока

Задание:

1. Рассчитать схему по законам Кирхгофа.

2. Определить токи в ветвях методом контурных токов.

3. Определить ток в ветви с сопротивлением R1 методом эквивалентного генератора.

4. Составить уравнение баланса мощностей и проверить его подстановкой числовых значений.

5. Определить показание вольтметра.

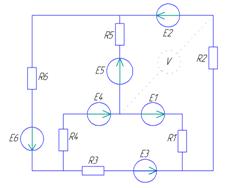
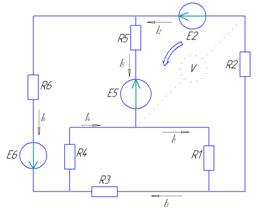
Расчет линейной цепи постоянного тока

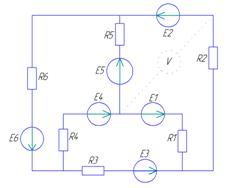
E2= -53B R1= 92Ом R4= 96Ом

E5= 51B R2= 71Ом R5= 46Ом

E6= -29B R3= 27Ом R6= 53Ом

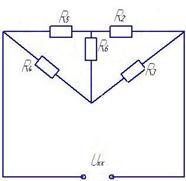
Расчёт схемы по законам Кирхгофа

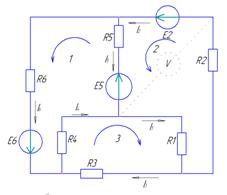
I1-6 – ?

Количество уравнений составляется по первому закону Кирхгофа (сумма входящих в узел токов равен сумме исходящих токов из узла)

n1=у-1=4–1=3; n1 – количество уравнений по 1-му закону Кирхгофа

у – число узлов

1. I6+I5 = I2

2. I5+I4=I1,

3. I3+I6= I4;

Составим уравнения по второму закону Кирхгофа (алгебраическая сумма падений напряжения в контуре равен алгебраической сумме ЭДС в этом же контуре.)

n2=B-у+1-BI=6–4+1=3; n2 – количество уравнений по 2-му закону Кирхгофа

В-число ветвей; В1 – число ветвей содержащих источник тока

I. – R5I5+R6I6+R4I4= E6 +E5,

II. R2I2 +R1I1 +R5I5 = E2 -E5,

III. R4I4+R1I1+R3I3=0;

96I4-46I5 +53I6= -29+51,

92I1+71I2+46I5= -53–51,

92I1 +27I3 +96I4 =0;

I2-I5-I6=0,

I4+I5-I1=0,

I3-I4+I6=0.

Решим систему уравнений с помощью Гаусса.

I1= -0,30609 А

I2= -0,76306 А

I3= 0,45697 А

I4= 0,16482 А

I5= -0,47091 А

I6= -0,29215 А

Метод контурных токов

Контурный ток – это некоторая величина, которая одинакова для всех ветвей контура.

I11, I22, I33 – ?

I11R11+I22R12…+…ImmR1m=E11

I11R21+I22R22…+…ImmR2m=E22

………………………………. – общий вид

I11Rm1+I22Rm2…+…ImmRmm = Emm

Для моего случая:

I11 R11 + I22 R12 +I33 R13 =E11

I11 R21+ I22 R22 +I33 R23= E22

I11 R31+ I22 R32+ I33 R33= E33

R11, R22, R33, – собственное сопротивление контуров, вычисляется как сумма сопротивления ветвей входящих в данный контур.

R11=R6+R5+R4

R22=R1+R5+R2

R33=R4+R3+R1

R12=R21, R13=R31, R23=R32 - общее сопротивление для 2-х контуров, вычисляется как сумма сопротивлений входящих в 2 смежных контура.

R12=R21=R5

R13=R31=R4

R23=R32=R1

E11, E22, E33 – собственная ЭДС контура, вычисляется как алгебраическая сумма всех входящих в контур ЭДС, причём ЭДС берется со знаком «+», если направление контура тока и ЭДС источника со направлены и «–» если противоположно направлены.

E11= E6 +E5

E22=E2 – E5

E33=0

I11(R6+R5+R4) – I22R5+I33R4= E6 +E5,

– I11R5+I22(R1+R5+R2)+I33R1=E2 –E5,

I11R4+I22R1+I33(R4+R3+R1)=0;

I11(53+46+96) – I2246+I3396= -29+51, 195 I11-46 I22 + 96 I33= 22,

– I1146+I22(92+46+71)+I3392=-53–51, -46 I11 +209 I22+92 I33= -104,

I1196+I2292+I33(96+27+92)=0; 96 I11+ 92 I22+215 I33= 0;

Решим систему уравнений с помощью Гаусса и найдем I1-6

I11= – 0,29215 A

I22= -0,76306 A

I33= 0,45697A

I6=I11= – 0,29215 А

I2=I22= -0,76306 A

I3= I33= 0,45697 A

I4=I11 + I33= 0,16482 A

I5= – I11 + I22= -0,47091 A

I1=I22+I33= -0,30609

Метод эквивалентного генератора

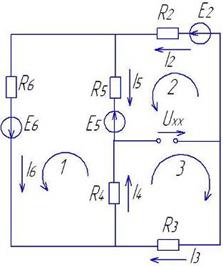
Разомкнем ветвь, в которой необходимо найти ток и представим эту разомкнутую цепь в виде эквивалентного генератора.

I1=EЭКВ /(R1+RВН); Rэк = RВН

Для определения напряжения холостого хода воспользуемся первым и вторым законами Кирхгофа.

R 11I’11+R12I’22= E5+E6,

R21I’11+R’22I’22= E2+E6,

(R4+R5+R6) I’11+R6I’22= E5+E6,

R6I’22+(R2+R3+R6)*I’22= E2+E6,

R4I’4xx+ R3I’3xx + Uxx= 0

UXX=(R1+RВН) I1

Определим внутреннее сопротивление эквивалентного генератора.

Воспользуемся методом входных сопротивлений, при этом сопротивление определяется относительно разомкнутой электрической цепи.

Для расчета из цепи устраняем все источники.

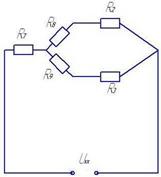
R7= R4*R5/(R4+R5+R6)=96*46/(96+46+53)=23 Ом

R8= R5*R6/(R4+R5+R6)=53*46/(96+46+53)=12,5 Ом

R9= R4*R6/(R4+R5+R6)=96*53/(96+46+53)=26 Ом

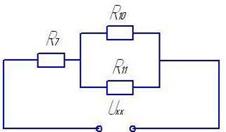
R8 и R2 соединены последовательно. R10=R7+R2= 83,5 Ом

R9 и R3 соединены последовательно. R11=R9+R3= 53 Ом

R10 и R11 соединены параллельно

R12=R11*R10/(R11+R10)=83,5*53/(83,5+53)=33,6 Ом

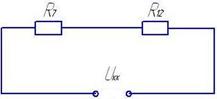
R7 и R12 соединены последовательно.

Rэк = RВН = R12+R7=33,6 + 23=56,6 Ом

195 I’11+53 I’22= 51–29

53 I’11+151 I’22=-53–29

I’11= I4xx

I’22 =-I3xx

I’11=I4xx= 0,28788 А

I’22=-I3xx= 0,64409 А

Uxx= – (R4I’4xx+ R3I’3xx)= – (96*0,28788 +27*0,6449)=-45,027 В

I'1=Uxx/(Rэк+R1)=(-45,027)/(56,6+92)= -0,30301 А

Баланс мощностей

∑ Pист = ∑ Pпотр

Pист=E2I2-E5I5+E6I6=(-52)*(-0,76306)+51*(-0,47091)+ (-29)*(-0,29215)= 72,9309 Вт

Pпотр=I12 R1+I22 R2+I32 R3+I24 R4+I52 R5+I62 R6=(-0,30609)2*92+(-0,76306)2 *71+(0,45697)2*27+ (0,16482)2 *96+(-0,47091)2 *46+(-0,29215)2 *53=72,9309Вт

72,9309=72,9309 баланс соблюдается

Определим показание вольтметра по закону Кирхгофа:

Uv+I5R5 =E2 – E5

Uv=E2 – I5R5 – E5 = – 53 – 51 – (-0,76306)*46= -69 В

pV= -69 В

2. Расчет электрической цепи однофазного переменного тока

Задание:

1. Определить комплексные действующие значения токов в ветвях схемы.

2. Определить показание приборов.

3. Составить баланс активных, реактивных и полных мощностей.

4. Повысить коэффициент мощности до 0,98 включением необходимого реактивного элемента Х.

5. Построить векторные диаграммы токов и напряжений в одной системе координат.

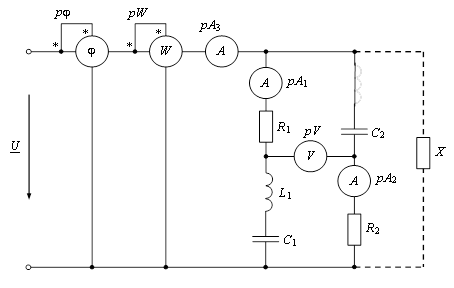
Расчет электрической цепи однофазного переменного тока

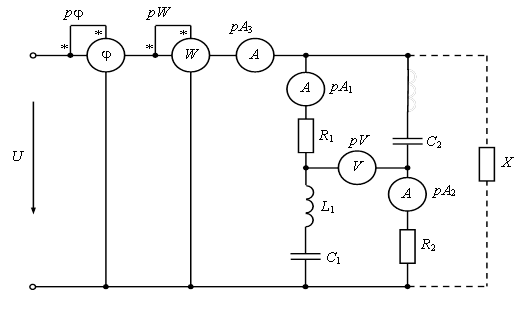
Исходные данные:

U=100В R1=24Ом L1=83мГн C1=230мкФ

F=200Гц R2=15Ом L2=0 C2=73мкФ

Определим комплексные действующие значения токов в ветвях схемы.

XL1=2π*FL1=2*3,14*200*83*10-3=104,25 Ом

XC1=1/(2π*FC1)= 1/(2*3.14*200*230*10-6)=3,46 Ом

XC2=1/(2π*FC2)= 1/(2*3.14*200*73*10-6)=10,91 Ом

Z1=R1+j(XL1-XC1)=24+j (104,25–3,46)=24+j100,79=103,6*ej76,6Ом

Z2=R2-jXС2=15-j10,91_=18,55*e-j36°Ом

I1=U/ Z1; I2=U/ Z2

I1=100ej0/103,6*ej76,6=0,96e-j76,6=0,96 (cos(-76,6)+j sin (-76,6))=(0,22 – j0,93) А

I2=100ej0/18,55*e-j36°=5,39ej36=5,39 (cos36+j sin36)=(4,36+j3,17) А

I3=I1+I2=0,22 – j0,93+4,36+j3,17=4,58+j2,24=5,1ej26,1ºА

2. Определим показание приборов

Показания амперметров:

pA1=I1=0,96A

pA2=I2=5,39A

pA3= I3=5,1A

Показание фазометра:

pφ= φu – φi3=0–26,1=-26,1°

Показание ваттметра

pW=Re [U*I3*]=100*5,1*cos (-26,1)=458 Вт

Показание вольтметра

Напряжение на вольтметре найдем по закону Кирхгофа:

I2R2 +UV – I1 j(XL1-XC1)=0

UV=I1 j(XL1-XC1) – I2R2

UV= j100,79 (0,22 – j0,93) – 15 (4,36+j3,17)=22,2j+93,73–65,4–47,55j=

=28,33–25,35j=38e-j41,8B

pV=38 B

3. Составим баланс активных, реактивных и полных мощностей

Sист. =Sпр.

Sист.=U.*I3*=100ej0*5,1e-j26,1º=510 e –j26,1°= (458 – j224,37) BA

Pист = 458Вт; Qист = -224,37 ВАр

Sпр = Pпр. +j Q пр.

Pпр=∑ I2R=I12R1+ I22R2=0,962*24+5,392*15=457,9 Вт

Qпр=∑ I2Х=I12XL1-I22XC1 -I32XC2=0,962*104,25–0,962*3,46–5,392*10,91= =-224,05 ВAр

Sпр = 457,9 - j 224,05=509,8e-j26,1 BA

510 e –j26,1°=509,8e-j26,1°баланс мощностей соблюдается. Искомые величины верны.

4. Повысить коэффициент мощности до 0,98 включением необходимого реактивного элемента Х. φ=-26,1 < 0

M(I) = 0,1; φx = arccos 0,98 = 11,48; φ = φu – φi

В данном случаем необходимо добавить индуктивность

L= U /(Ix*ω)

Ix= I3*sinφ – I3*cosφ*tgφx

Ix= 5,1*sin (26,1) – 5,1*cos (26,1)*tg11,48=1,3135A

L= 100 /(1,3135*1256)=60,62 мГн

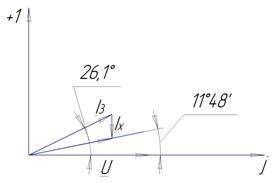
5. Построение векторных диаграмм токов и напряжений в одной системе координат

UR1=I1*R1=0,96e-j76,6*24=23,04e-j76,6 В

UL1=I1*jXL1=0,96 e-j76,6*j104,25=[0,96cos (-76,6)+j0,96sin (-76,6)] (j104,25)=

=(0,22-j0,93) (j104,25)=99,63 ej13,3 В

UC1=I1*(-jXC1)=0,96 e-j76,6*(-j3,46)= [0,96cos (-76,6)+j0,96sin (-76,6)] (-j3,46)=

=3,31 ej(13,3+180)= 3,31 ej193,3В

UR2=I2*R2=5,39 ej36*15=80,85 ej36В

UC2=I2*(-jXC2)=5,39 ej36*(-j10,91)=(5,39cos36+5,39sin36) (-j10,91)=

=(4,36+j3,17) (-j10,91)= 58,8 e-j54 В

Масштабы:

МU=1 В/мм

МI=0,2 А/мм