
Рефераты по рекламе
Рефераты по физике
Рефераты по философии
Рефераты по финансам
Рефераты по химии
Рефераты по хозяйственному праву
Рефераты по экологическому праву
Рефераты по экономико-математическому моделированию
Рефераты по экономической географии
Рефераты по экономической теории
Рефераты по этике
Рефераты по юриспруденции
Рефераты по языковедению
Рефераты по юридическим наукам
Рефераты по истории
Рефераты по компьютерным наукам
Рефераты по медицинским наукам
Рефераты по финансовым наукам
Рефераты по управленческим наукам
Психология педагогика
Промышленность производство
Биология и химия
Языкознание филология
Издательское дело и полиграфия
Рефераты по краеведению и этнографии
Рефераты по религии и мифологии
Рефераты по медицине
Контрольная работа: Определение реакций опор составной конструкции
Контрольная работа: Определение реакций опор составной конструкции
Задание С-3. Определение реакций опор составной конструкции
Вариант № 1.
Найти реакции опор и давление в промежуточном шарнире составной конструкции. Схема конструкции представлена на рис. 1 (размеры – в м), нагрузка указана в таблице 1.
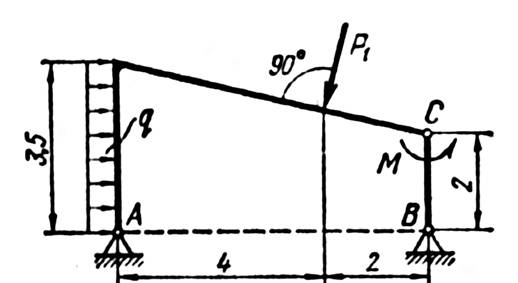
Рис. 1
Таблица 1.
| P1, кН | М, кН×м | q, кН/м |
| 6,0 | 25,0 | 0,8 |
С-3. Определение реакций опор составной конструкции
Решение. Рассмотрим систему уравновешивающихся
сил,  приложенных ко всей конструкции (рис.
2).
приложенных ко всей конструкции (рис.
2).
y
P1y P1
90°
P1x C
Q M
RAy RBy
RAx RBx x
A B
Рис. 2.
Разложим силу P на составляющие Px и Py.
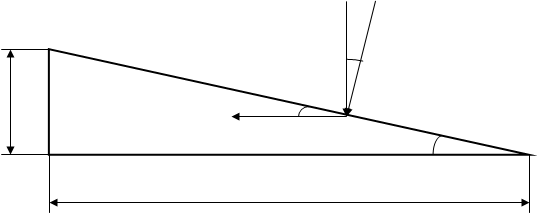
P1y P1
a
P1x a a
6
Рис. 3.
P1x = P1×sin(a),
P1y = P1×cos(a).
a = arctg(1,5/6) = arctg(0,25) = 14°.
P1x = P1×sin(a) = P1×sin(14°) = 6×0,24 = 1,44 (кН),
P1y = P1×cos(a) = P1×cos(14°) = 6×0,97 = 5,82 (кН).
Q = q×3,5 = 0,8×3,5 = 2,8 (кН).
С-3. Определение реакций опор составной конструкции.
Запишем уравнения равновесия:
![]()
![]() (1)
(1)
![]()
![]() (2)
(2)
![]()
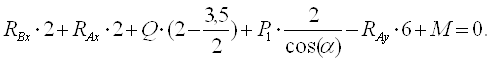 (3)
(3)
Данная система из 3 уравнений содержит 4 неизвестных, для их нахождения рассмотрим отдельно правую и левую части конструкции.
Рассмотрим систему уравновешивающихся сил, приложенных к левой части конструкции (рис.4):
 y
y
P1y P1
90°
P1x C
RCx
Q RCy
RAy
RAx x
A
Рис. 4.
Запишем уравнения равновесия:
![]()
![]() (4)
(4)
![]()
![]() (5)
(5)
С-3. Определение реакций опор составной конструкции
![]()
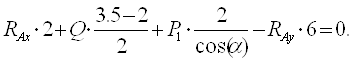 (6)
(6)
Рассмотрим систему уравновешивающихся сил, приложенных к правой части конструкции (рис.5):
 y
y
R`Cy
R`Cx
C
M
RBy
RBx x
B
Рис.5.
Запишем уравнения равновесия:
![]()
![]() (7)
(7)
![]()
![]() (8)
(8)
![]()
![]() (9)
(9)
где RCx = R`Cx, RCy = R`Cy.
Таким образом, имеем систему 4 уравнений (1), (2), (6) и (9) с 4 неизвестными.
Из уравнения (9)
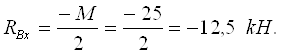
Из уравнения (1)
![]()
С-3. Определение реакций опор составной конструкции
Из уравнения (6)

Из уравнения (2)
![]()
Найдем реакции шарнира С:
RCx = -RBx = 12,5 кН,
RCy = -RBy = 0,07 кН.
Отрицательные значения RBx и RBy говорят о том, что действительное направление RBx и RBy противоположно указанному на рис.4.
Итак,
С-3. Определение реакций опор составной конструкции
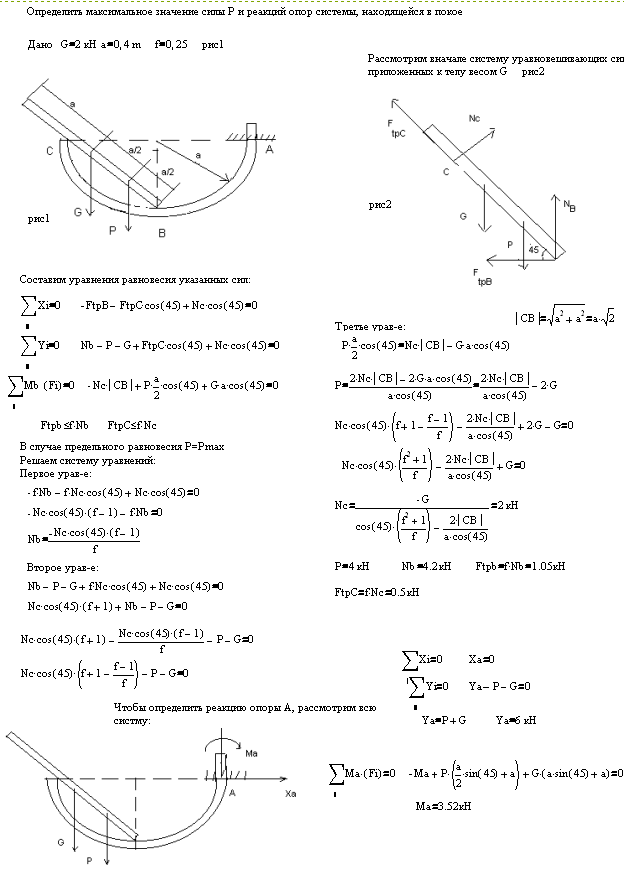
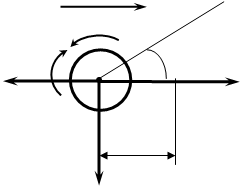
Найти реакции опор конструкции изображенной на рис.1.
|
|
|
|
Дано: Q = 2, G = 20, a = 20, b = 30, c = 10 R =15, r =5. Решение: Разложим реакции в опорах А и Б на их составляющие по осям коардинат, при этом RAy=RBy=RDy=0 |
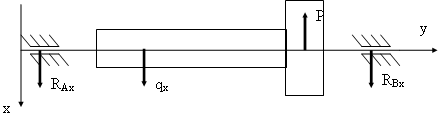
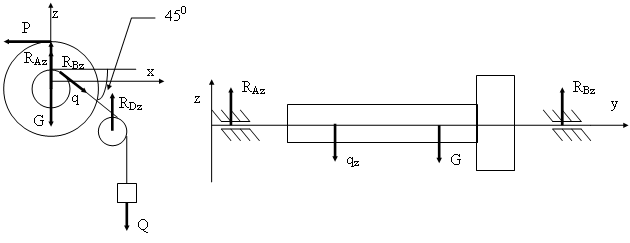
Составим уравнения сумм моментов относительно всех осей:
Р*15-q*5=0, где , отсюда Р=(q*5)/15
-qx*20+P*60-RBx*80, отсюда RBx=(qx*20-P*60)/80
-qx*20-G*(20+30)+RBz*(20+30+30) отсюда RBz= (qx*20+G*50)/80
-Raz*80+qz*60+G*30=0 отсюда Raz= (qz*60+G*30)/80
Rax*80+ qx*60-P*30=0 отсюда Rax=-( qx*60-P*30)/80
qx=Q*cos45; qz=Q*sin45
Ra= RB=
Результаты работы
|
Raz |
Rax |
Ra |
RBz |
RBx |
RB |
Применение теоремы об изменении кинетической энергии к изучению движения механической системы.
Вариант № 1.
Механическая система под действием сил тяжести приходит в движение из состояния покоя; начальное положение системы показано на рис. 1. Учитывая трение скольжения тела 1, пренебрегая другими силами сопротивления и массами нитей, предполагаемых нерастяжимыми, определить скорость тела 1 в тот момент, когда пройденный им путь станет равным s.
В задании приняты следующие обозначения: m1, m2, m3, m4 – массы тел 1, 2, 3, 4; b - угол наклона плоскости к горизонту; f – коэффициент трения скольжения.
Необходимые для решения данные приведены в таблице 1. Блоки и катки считать сплошными однородными цилиндрами. Наклонные участки нитей параллельны соответствующим наклонным плоскостям.
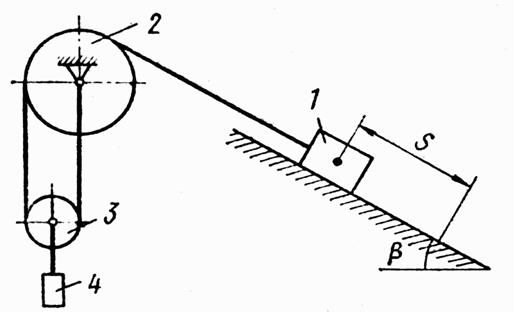
Рис. 1
Таблица 1.
| m1, кг | m2, кг | m3, кг | m4, кг | b, град | f | s, м |
| m | 4m | 0,2m | 4m/3 | 60 | 0,10 | 2 |
Решение.
Применим теорему об изменении кинетической энергии системы:
![]() (1)
(1)
где T0 и T – кинетическая энергия
системы в начальном и конечном положениях; ![]() - сумма работ внешних сил,
приложенных к системе;
- сумма работ внешних сил,
приложенных к системе; ![]() - сумма работ внутренних сил
системы.
- сумма работ внутренних сил
системы.
Для рассматриваемых систем, состоящих из абсолютно твердых тел, соединенных нерастяжимыми нитями,
![]()
Так как в начальном положении система находится в покое, то Т0=0.
Следовательно, уравнение (1) принимает вид:
![]() (2)
(2)
Кинетическая энергия рассматриваемой системы Т в конечном ее положении (рис.2) равна сумме кинетических энергий тел 1, 2, 3 и 4:
Т = Т1 + Т2 + Т3 + Т4. (3)
 2
2
1
w2
VA
V3
3 b V1
A C3 CV
w3
V4
4
Рис. 2.
Д-10
Кинетическая энергия груза 1, движущегося поступательно,
![]() (4)
(4)
Кинетическая энергия барабана 2, совершающего вращательное движение,
![]() , (5)
, (5)
где J2x – момент инерции барабана 2 относительно центральной продольной оси:
![]() , (6)
, (6)
w2 – угловая скорость барабана 2:
![]() . (7)
. (7)
После подстановки (6) и (7) в (5) выражение кинетической энергии барабана 2 принимает вид:
![]() . (8)
. (8)
Кинетическая энергия барабана 3, совершающего плоское движение:
![]() , (9)
, (9)
где VC3 – скорость центра тяжести С3 барабана 3, J3x – момент инерции барабана 3 относительно центральной продольной оси:
![]() , (10)
, (10)
w3 – угловая скорость барабана 3.
Так как двигается по нити без скольжения, то мгновенный центр скоростей находится в точке СV. Поэтому
![]() , (11)
, (11)
![]() . (12)
. (12)
Подставляя (10), (11) и (12) в (9), получим:
![]() . (13)
. (13)
Кинетическая энергия груза 4, движущегося поступательно,
![]() , (14)
, (14)
где V4 = VC3 = V1/2:
![]() . (15)
. (15)
Кинетическая энергия всей механической системы определяется по формуле (3) с учетом (4), (8), (13), (15):
![]()
Подставляя и заданные значения масс в (3), имеем:
![]()
или
![]() . (16)
. (16)
Найдем сумму работ всех внешних сил, приложенных к системе, на заданном ее перемещении (рис. 3).
 2
2
1
N1
FTP
3 b
C3
P3 P1
4
P4
Рис. 2.
Работа силы тяжести ![]() :
:
![]() (17)
(17)
Работа силы трения скольжения ![]() :
:
![]()
Так как
![]()
то
![]() (18)
(18)
Работа силы тяжести ![]() , препятствующей
движению тела 1:
, препятствующей
движению тела 1:
![]() (19)
(19)
Работа силы тяжести ![]() ,
препятствующей движению тела 1:
,
препятствующей движению тела 1:
![]() (20)
(20)
Сумма работ внешних сил определится сложением работ, вычисляемых по формулам (17) – (20):
![]() .
.
Подставляя заданные значения масс, получаем:
![]()
или
![]() . (21)
. (21)
Согласно теореме (2) приравняем
значения Т и ![]() , определяемые по формулам (16) и
(21):
, определяемые по формулам (16) и
(21):
![]() ,
,
откуда
![]() м/с.
м/с.
Д-10
Задание Д-19. Применение общего уравнения динамики к исследованию движения механической системы с одной степенью свободы.
Вариант № 1.
Для заданной механической системы определить ускорения грузов и натяжения в ветвях нитей, к которым прикреплены грузы. Массами нитей пренебречь. Трение качения и силы сопротивления в подшипниках не учитывать. Система движется из состояния покоя.
Необходимые для решения данные приведены в таблице 1. Блоки и катки, для которых радиусы инерции в таблице не указаны, считать сплошными однородными цилиндрами.
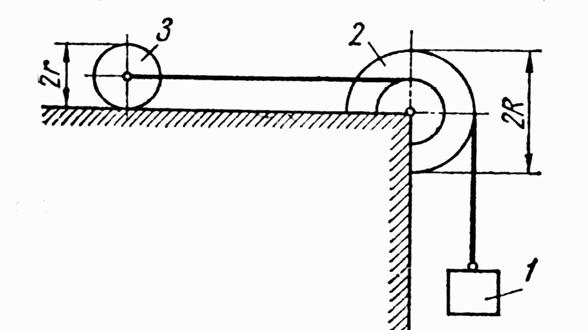
Рис. 1
Таблица 1.
|
G1, кг |
G2, кг |
G3, кг |
R/r |
i2x |
| G | G | 3G | 2 |
|
Решение.
Применим к решению задания общее уравнение динамики. Так как система приходит в движение из состояния покоя, направления ускорений тел соответствуют направлениям их движения. Движение таково, что груз 1 опускается.
Покажем задаваемые силы: силы
тяжести ![]() -
груза 1,
-
груза 1, ![]() -
блока 2 и
-
блока 2 и ![]() -
катка 3 (рис. 2).
-
катка 3 (рис. 2).
a3

M3Ф 2 e2 M3Ф
Ф3 e3 dj3
dj2
ds3
3
G3
Ф1
G2 1
a1
ds3
G1
Рис. 2.
Приложим силы инерции. Сила
инерции груза 1, движущегося поступательно с ускорением ![]() :
:
![]() .
.
Силы инерции блока 2, вращающегося вокруг неподвижной оси с угловым ускорением e2, приводятся к паре, момент которой
![]()
![]()
Силы инерции катка 3, совершающего плоское движение, приводятся к силе
![]() ,
,
где ![]() - ускорение центра масс катка 3,
и к паре сил, момент которой
- ускорение центра масс катка 3,
и к паре сил, момент которой
![]() ,
,
где e3 – угловое ускорение катка 3, J3 – момент инерции катка 3 относительно центральной продольной оси:
![]() .
.
Сообщим системе возможное перемещение в направлении ее действительного движения (рис. 2). Составим общее уравнении динамики:
![]() , (1)
, (1)
где dj2 и dj3 – углы поворотов блоков 2 и 3.
Учитывая, что G1 = G2 = G = mg, G3 = 3G = 3mg
имеем:
![]()
![]()
![]()
![]() (2)
(2)
![]()
Устанавливаем зависимости между возможными перемещениями, входящими в (1), и между ускорениями в (2), пользуясь тем, что эти зависимости такие же, как между соответствующими скоростями:
![]() dj2 = dj3 = ds1/R = ds1/2r;
dj2 = dj3 = ds1/R = ds1/2r;
ds3 = dj2r = ds1/2; (3)
e2 = e3 = a1/2r; a3 = a1/2.
С учетом (2) и (3) уравнение (1), после деления всех его членов на m и ds1, принимает вид
![]()
откуда
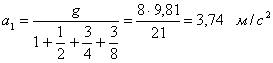 ,
,
а3 = a1/2 = 1,87 м/с2.
 а3
а3
M3Ф
Ф3 e3 dj3 Т2-3
ds3
G3
Рис. 3.
 Ф1
Ф1
Т1-2
а1
ds1
G1
Рис. 4.
Для определения натяжения в нити 2-3 мысленно разрежем эту нить и заменим ее действие на каток 3 реакцией T2-3 (рис. 3).
Общее уравнение динамики:
![]() ,
,
откуда
![]()
Для нахождения натяжения в нити 1-2 мысленно разрежем эту нить и заменим ее действие на груз 1 реакцией T1-2 (рис. 4).
Не составляя общего уравнения динамики, на основании принципа Даламбера имеем:
![]()
Задание К-3. Определение скоростей и ускорений точек твердого тела при плоском движении.
Вариант № 1.
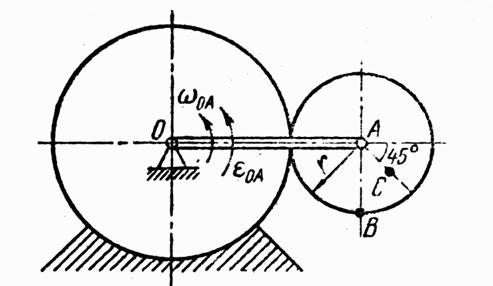
Рис. 1
Найти для заданного положения механизма скорости и ускорения точек В и С. Схема механизма представлена на рис. 1, необходимые для расчета данные приведены в таблице 1.
Таблица 1.
|
Размеры, см |
wОА, с-1 |
eОА, с-2 |
||
|
ОА |
r |
АС |
||
|
40 |
15 |
8 |
2 |
2 |
Решение.
Определение скоростей точек.
Вычислим скорость точки А при заданном положении механизма:
VA = wОА×OA = 2×40 = 80 см/с.
Скорость точки А направлена перпендикулярна к ОА. Мгновенный центр скоростей СV находится в точке соприкосновения колес.
Угловая скорость колеса
wК = VA/r = 80/15 = 5,33 c-1
Скорости точек В и С:
VB = wК×ВСV;
VС = wК×ССV,
где
ВСV = r×![]() = 15×1,41
= 21,2 см,
= 15×1,41
= 21,2 см,
ССV = ![]() см.
см.
Следовательно,
VB = wК×ВСV = 5,33×21,2 = 113 см/с;
VС = wК×ССV = 5,33×21,4 = 114,1 см/с.
Вектор ![]() направлен перпендикулярно к
отрезку BCV, а вектор
направлен перпендикулярно к
отрезку BCV, а вектор ![]() - перпендикулярно к отрезку CCV в
сторону вращения колеса.
- перпендикулярно к отрезку CCV в
сторону вращения колеса.
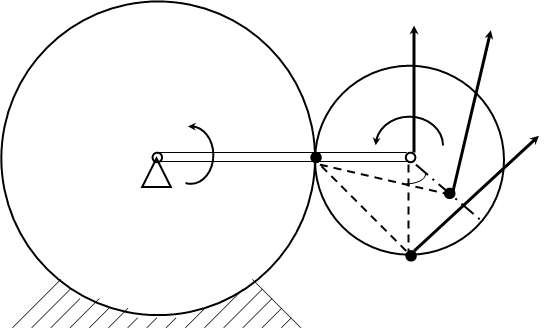 VA
VA
VC
wК
O wOA CV A VB
45°
C
r
B
Рис. 2
К-3
Определение ускорений точек.
Ускорение точки А складывается из вращательного и центростремительного ускорений:
![]() ;
;
![]() см/с2;
см/с2;
![]() см/с2.
см/с2.
Вектор ![]() направлен от А к О. Вектор
направлен от А к О. Вектор ![]() перпендикулярен
к вектору
перпендикулярен
к вектору ![]() и
направлен в соответствии с направлением углового ускорения eОА.
и
направлен в соответствии с направлением углового ускорения eОА.
Согласно теореме об ускорениях точек плоской фигуры имеем:
![]() .
.
Центростремительное ускорение точки В во вращательном движении колеса вокруг полюса А:
![]() см/с2.
см/с2.
Вращательное ускорение точки В:
![]() ,
,
где
![]() с-2,
с-2,
![]() см/с2.
см/с2.
Вектор ![]() направлен от В к А. Вектор
направлен от В к А. Вектор ![]() перпендикулярен
к вектору
перпендикулярен
к вектору ![]() и
направлен в соответствии с направлением углового ускорения eK.
и
направлен в соответствии с направлением углового ускорения eK.
Ускорение точки В находим способом проекций:
![]() см/с2;
см/с2;
![]() см/с2;
см/с2;
![]() см/с2.
см/с2.
Определяем ускорение точки С:
![]() .
.
Центростремительное ускорение точки С во вращательном движении колеса вокруг полюса А:
![]() см/с2.
см/с2.
К-3
Вращательное ускорение точки С:
![]() см/с2.
см/с2.
Вектор ![]() направлен от С к А. Вектор
направлен от С к А. Вектор ![]() перпендикулярен
к вектору
перпендикулярен
к вектору ![]() и
направлен в соответствии с направлением углового ускорения eK.
и
направлен в соответствии с направлением углового ускорения eK.
Ускорение точки С находим способом проекций:
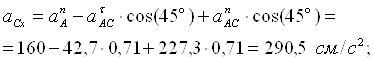
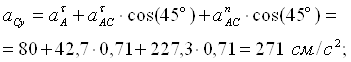
![]() см/с2.
см/с2.
 y
y
aC aCy
aBy
aB
aAt
eOA eK aACt
x O aAn A
aACn
C
aCx 45°
aABn
aBx B aABt
Рис. 3
К-3
Задание K-1. Определение скорости и ускорения точки по заданным уравнениям ее движения.
Вариант № 1.
По заданным уравнениям движения точки М установить вид ее траектории и для момента времени t = t1(c) найти положение точки на траектории, ее скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории в соответствующей точке. Данные приведены в таблице 1.
Таблица 1.
| Уравнения движения |
t1(c) |
|
| x = x(t), см | y = y(t), см | |
|
-2t2+3 |
-5t |
0,5 |
K-1
Решение.
Исходные данные в см и с:
x = -2t2 + 3; y = -5t; (1)
t1 = 0,5
Уравнения движения (1) являются параметрическими уравнениями траектории точки М. Чтобы получить уравнение траектории в обычной координатной форме, исключим время t из уравнений движения. Тогда
25x + 2y2 = 75 (2)
Это уравнение параболы.
Для определения скорости точки находим проекции скорости на оси координат:
Vx = x’ = -4t см/с; Vy = y’ = -5 см/с.
Модуль скорости точки
![]() .
(3)
.
(3)
Аналогично проекции ускорения точки
ax = x’’ = -4 см/с2; ay = y’’ = 0.
Модуль ускорения точки
![]() см/с2.
см/с2.
Касательное ускорение находим путем дифференцирования модуля скорости (3)
![]()
![]()
При t = 0,5 c
x = -2×0,52 + 3 = 2,5 см, y = -5×0.5 = -2,5 см.
Vx = -4×0,5 =-2 см/с, Vy = -5 см/с, V = 5,38 см/с.
ax = -4 см/с2, ay = 0, a = 4 см/с2
![]() см/с2
см/с2
K-1
Модуль касательного ускорения
at = 1,487 см/с2
Знак “+” при dV/dt показывает,
что движение точки ускоренное и, следовательно, направления ![]() совпадают.
совпадают.
Нормальное ускорение точки:
![]() см/с2.
см/с2.
Радиус кривизны траектории в той точке, где при t = 0,5 с находится точка М:
![]() см.
см.
Пользуясь уравнением (2), строим
траекторию (рис. 1) и показываем на ней положение точки М в заданный момент
времени. Вектор ![]() строим по составляющим
строим по составляющим ![]() , причем он
направлен по касательной к траектории точки. Вектор
, причем он
направлен по касательной к траектории точки. Вектор ![]() находим как по составляющим
находим как по составляющим ![]() , так и по
, так и по ![]() .
.
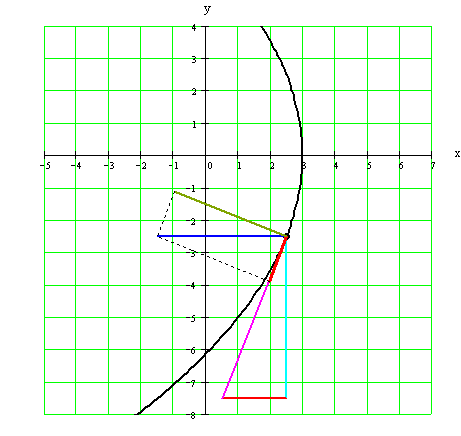 |
Рис. 1
Задание К-2. Определение скоростей и ускорений точек твёрдого тела при поступательном и вращательном движениях.
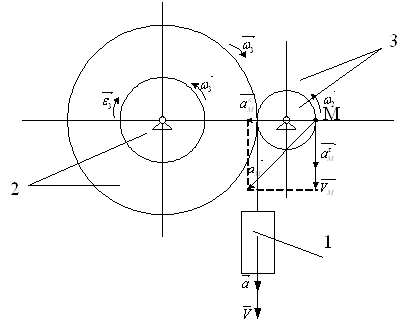 Вариант № 1.
Вариант № 1.
Дано:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Определить коэффициенты ![]() ,
, ![]() и
и ![]() , при которых
осуществляется требуемое движение груза 1. Определить так же в момент времени
, при которых
осуществляется требуемое движение груза 1. Определить так же в момент времени ![]() скорость и
ускорение груза и точки М одного из колёс механизма.
скорость и
ускорение груза и точки М одного из колёс механизма.
Решение:
Уравнение движения груза 1 имеет вид:
![]() (1).
(1).
Коэффициенты ![]() ,
, ![]() и
и ![]() могут быть определены
из следующих условий:
могут быть определены
из следующих условий:
при ![]()
![]()
![]() (2).
(2).
при ![]()
![]() (3).
(3).
Скорость груза 1:
![]() (4).
(4).
Подставляя (2) и (3) в формулы (1) и (4), находим коэффициенты:
![]()
![]()
![]()
Таким образом уравнение движения груза 1:
![]() (5).
(5).
Скорость груза 1:
![]() (6).
(6).
Ускорение груза 1:
![]()
Для определения скорости и
ускорения точки М запишем уравнения, связывающие скорость груза ![]() и угловые скорости
колёс
и угловые скорости
колёс ![]() и
и ![]() .
.
В соответствии со схемой механизма
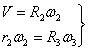 (7).
(7).
откуда
![]()
или с учётом (6) после подстановки данных:
![]()
Угловое ускорение колеса 3:
![]()
Скорость точки М, её вращательное, центростремительное и полное ускорения определяются по формулам:
![]()
![]()
![]()
![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Выполнил: ст.гр. С-045 rus Калайчиди Виктор
Проверил: Русу В.Н.
| Шифр | Вариант |
| 61 | 16 |
![]() Дано:
схема механизма,
Дано:
схема механизма,
Sr=OM=20 sin рt см
t1=1/3 c
a=20 cм
Решение:
Положение М на фигуре D определяется расстоянием Sr=OM
При t=1/3 c
Sr=20 sin р/3 =17.32 cм
Абсолютная скорость точки М
V=Vr+Ve
Модуль относительной скорости
Vr=| Vr |
Vr=dSr/dt=20р cos рt
При t=1/3 c
Vr=10 р=31.41 cм/с
Положительный знак у величины Vr показывает, что вектор Vr направлен в сторону возрастания Sr
Модуль переносной скорости
Ve=Rщe
R= Sr2+a2 =26.46 см
щe=|щe| щe=dцe/dt=1-t c-1
При t=1/3
щe= 0.67 c-1
Положительный знак у величины щe показывает, что вращение фигуры D происходит вокруг Оz по направлению отсчета угла ц. Вектор щe направлен на наблюдателя.
Переносная скорость
Ve=17.73 см/с
Вектор Ve направлен по касательной к окружности вращения т.М
Из теоремы косинусов найдём
V=Vr2+ Ve2 - 2VrVeсos б
cos б = a/R = 0.76
V=21.32 cм/с
Абсолютное ускорение точки равно геом. сумме относительного, переносного, и кориолисова ускорений
W=Wr+We+Wc
W=Wrф+Wrn+Weв +Weц+Wc
Wrф= d2Sr/dt2 =-20р2 sin рt
При t=1/3 c
Wrф= -170.77 cм/с2
Wrф=170.77 cм/с2
Знак “-“ показывает, что Wrф направлен в сторону убывания Sr
Wrn=Vr2/с=0 (с=∞)
Модуль переносного вращательного ускорения
Weв=Rеe
еe= d2цe/dt2=-1 c-2
Weв= -26.46 cм/с2
Разные знаки у величин еe и щe говорят о замедленном движении круга D, вектора еe и щe противоположно направленны.
Weц=R щe2=11.88 cм/с2
Вектор Weц направлен к центру окружности L
Wc=2щe x Vr
Wc=2щeVr sin(щe Vr)
sin(щe Vr)=1
Wc=2щeVr=48.09 cм/с2
По методу проекций имеем
Wx= Weв cos б - Weц cos(90-б) - Wrф=
Wy= Wc-Weв sin б - Weц sin(90-б) =
W= Wx2+ Wy2=
|
щe, c-1 |
Скорость, см/с |
еe,c-2 |
Ускорение, см/с2 |
|||||||||||
|
Vr |
Ve |
V |
Wrф |
Wrn |
Weв |
Weц |
Wc |
Wx |
Wy |
W | ||||
| 0.67 | 31.41 | 17.73 | 21.32 | -1 | -170.77 | 0 | -26.46 | 11.88 | 48.09 | |||||