Курсовая работа: Теория относительности

Курсовая работа: Теория относительности

Государственное образовательное учреждение

Высшего профессионального образования

Сибирский государственный аэрокосмический университет имени академика М. Ф. Решетнева

Институт машиноведения и инноватики

Кафедра управления качеством и сертификации

Курсовая работа

по дисциплине «Концепции современного естествознания»

Тема: «Теория относительности»

Выполнил:

Студент группы МЗУ 81/2

Богатырёв М. О.

Проверил: Доц., к.ф.н.

Жирнова Е. А.

Содержание

1.  Введение

2.  Общая теория относительности (ОТО)

2.1 История создания общей теории относительности

2.2 Принцип равенства гравитационной и инертной масс

2.3 Принцип движения по геодезическим линиям

2.4 Кривизна пространства-времени

2.5 Пространство-время ОТО и сильный принцип эквивалентности

2.6 Основные следствия ОТО

3.   Экспериментальные подтверждения ОТО

3.1 Эффекты, связанные с ускорением систем отсчёта

3.2 Гравитационное отклонение света

3.3 Чёрные дыры

3.4 Орбитальные эффекты

3.5 Увлечение инерциальных систем отсчёта

3.6 Другие предсказания

4.   Космология

5.   Проблемы ОТО

5.1 Проблема энергии

5.2 ОТО и квантовая физика

6.  Специальная теория относительности (СТО)

6.1 Создание СТО

7.  Постулаты Эйнштейна

8.   Сущность СТО

8.1 Четырёхмерный континуум — пространство-время

9.  Отношения теории относительности с другими физическими понятиями

9.1 Гравитация

9.2 Классическая механика

9.3 Квантовая механика

10.   Эффекты СТО

10.1 Замедление времени

10.2 Сокращение линейных размеров

10.3 О релятивистской массе

11.   Исторический очерк

12.   Заключение

13. Список литературы

1. Введение

Теория относительности — общепринятая официальной наукой теория о том, как устроен мир (на макроуровне), объединяющая механику, электродинамику и гравитацию. Содержанием теории относительности является физическая теория пространства и времени, учитывающая существующую между ними взаимосвязь геометрического характера.

Название же “принцип относительности” или “постулат относительности”, возникло как отрицание представления об абсолютной неподвижной системе отсчета, связанной с неподвижным эфиром, вводившимся для объяснения оптических и электродинамических явлений. Принцип относительности - фундаментальный физический закон, согласно которому любой процесс протекает одинаково в изолированной материальной системе, находящейся в состоянии покоя, и в такой же системе в состоянии равномерного прямолинейного движения. Состояния движения или покоя определяются по отношению к произвольно выбранной инерциальной системе отсчета. Принцип относительности лежит в основе специальной теории относительности Эйнштейна. Внедрена теория в научные круги Альбертом Эйнштейном. Основоположниками данной теории также считаются Г.А. Лоренц и А. Пуанкаре.

Основным отличием представлений о пространстве и времени теории относительности от представлений ньютоновской физики является ограниченная взаимосвязь пространства и времени. Эта взаимосвязь раскрывается в формулах преобразования координат и времени при переходе от одной системе отсчета к другой (преобразования Лоренца).

Вообще каждое физическое явление протекает в пространстве и времени и не может быть изображено в нашем сознании иначе, как в пространстве и во времени. Пространство и время суть формы существования материи. Никакой материи не существует вне пространства и времени. Конкретным изображением пространства и времени является система отсчета, т.е. координатно-временное многообразие чисел составляющие воображаемую сетку и временную последовательность всех возможных пространственных и временных точек. Одно и то же пространство и время могут изображаться различными координатно-временными сетками (системами отсчета). Существует фактически две различных теории относительности, известных в физике, одна из них называется специальной (частной) теорией относительности, другая - общей теорией относительности. Альберт Эйнштейн предложил первую из них в 1905 г., вторую - в 1916 г. Принимая во внимание, что специальная теория относительности связана, в первую очередь, с электрическими и магнитными явлениями и с их распространением в пространстве и времени, общая теория относительности была разработана, прежде всего, чтобы иметь дело с тяготением. Обе теории сосредотачиваются на новых подходах к пространству и времени, подходах, которые отличаются глубоко от тех, которые используются в каждодневной жизни; но релятивистские понятия пространства и времени неразрывно вплетаются в любую современную интерпретацию физических явлений в пределах от атома до вселенной в целом.

Рассмотрим последовательное развитие этих теорий.

2. Общая теория относительности

О́бщая тео́рия относи́тельности (ОТО) — геометрическая теория тяготения, развивающая специальную теорию относительности (СТО), опубликованная Альбертом Эйнштейном в 1915—1916 годах. В рамках общей теории относительности, как и в других метрических теориях, постулируется, что гравитационные эффекты обусловлены не силовым взаимодействием тел и полей, находящихся в пространстве-времени, а деформацией самого пространства-времени, которая связана, в частности, с присутствием массы-энергии. Общая теория относительности отличается от других метрических теорий тяготения использованием уравнений Эйнштейна для связи кривизны пространства-времени с присутствующей в нём материей.

2.1 История создания общей теории относительности

До теории относительности в физике было две прекрасно работающих по отдельности области: механика Ньютона, миллионы раз проверенная экспериментом, и электродинамика, сравнительно молодая, но уже крепко стоящая на ногах наука, описывающая в том числе распространение электромагнитных волн. Распространение волн описывалось уравнениями Максвелла, которые тоже были многократно проверены экспериментом и сомнений не вызывали. Тогда уже было известно, что свет — это тоже электромагнитная волна, и, следовательно, скорость распространения электромагнитных волн равна скорости света. Но каждый раз, попытки измерить скорость в динамичной системе заканчивались провалом. Исходя из постулатов теории Ньютона - скорость света и скорость источника света необходимо было суммировать, но уравнения Максвелла не позволяли создать такую математическую модель, а попытки их доработать, чтобы подстроить под такую ситуацию, заканчивались крахом. Например: если лететь за светом со скоростью равной скорости света — то этот свет по уравнениям Максвелла исчезал.

XIX век был веком механики, вследствие чего все явления стремились описать при помощи механических моделей. Эфир является одной из таких моделей, предназначенной сперва для описания электродинамики, а позднее — и гравитации, а также строения элементарных частиц.

По сути, эфиродинамика была первой попыткой создать полевую теорию всего, и не самой плохой: и уравнения Максвелла, и даже преобразования Лоренца успешно выводились и обосновались исходя из положений эфиродинамики. Даже многие сугубо квантовые эффекты, например, планковский спектр излучения, в этой модели вполне объяснимы силами классической физики.

В наиболее простых моделях считалось, что эфир и материя — различные вещи, и первый не оказывает материи никакого сопротивления, поэтому законы Ньютона для движущихся тел какими были, такими и остаются, а уравнения Максвелла справедливы только в системе отсчета, которая статична относительно эфира. Такое решение всех устроило бы, но из него следовал один важный вывод: солнечная система, двигаясь с гигантскими скоростями в космосе, несётся сквозь эфир, поэтому можно поставить эксперимент по обнаружению этого «эфирного ветра». Майкельсон и Морли ставят такой опыт, и результат этого опыта породил сомнения физиков в существовании эфира. После физического конгресса 1900 г. в Париже, где лорд Кельвин заявил о «нулевом» результате эфирного опыта.

Классическая теория тяготения Ньютона основана на понятии силы тяготения, которая является дальнодействующей силой: она действует мгновенно на любом расстоянии. Этот мгновенный характер действия несовместим с понятием поля в современной физике. В теории Эйнштейна никакая информация не может распространиться быстрее скорости света в вакууме.

Математически сила гравитации Ньютона выводится из потенциальной энергии тела в гравитационном поле. Потенциал гравитации, соответствующий этой потенциальной энергии, подчиняется уравнению Пуассона, которое не инвариантно при преобразованиях Лоренца. Причина неинвариантности заключается в том, что энергия в специальной теории относительности не является скалярной величиной, а переходит во временную компоненту 4-вектора. Векторная же теория гравитации оказывается аналогичной теории электромагнитного поля Максвелла и приводит к отрицательной энергии гравитационных волн, что связано с характером взаимодействия: одноимённые заряды (массы) в гравитации притягиваются, а не отталкиваются, как в электромагнетизме. Таким образом, теория гравитации Ньютона несовместима с фундаментальным принципом специальной теории относительности — инвариантностью законов природы в любой инерциальной системе отсчёта, а прямое векторное обобщение теории Ньютона, впервые предложенное Пуанкаре в 1905 году в его работе «О динамике электрона», приводит к физически неудовлетворительным результатам.

Инерциальные системы отсчёта (ИСО) — это системы отсчёта, в которых точечное тело, на которое не действуют никакие силы, сохраняет свое состояние покоя или равномерного прямолинейного движения. Постулаты СТО формулируются именно для таких систем отсчёта, как, впрочем, и три закона Ньютона в ньютоновой механике.

Эйнштейн начал поиск теории гравитации, которая была бы совместима с принципом инвариантности законов природы относительно любой системы отсчёта. Результатом этого поиска явилась общая теория относительности, основанная на принципе тождественности гравитационной и инертной массы.

2.2 Принцип равенства гравитационной и инертной масс

В нерелятивистской механике существует два понятия массы: первое относится ко второму закону Ньютона, а второе — к закону всемирного тяготения. Первая масса — инертная (или инерционная) — есть отношение негравитационной силы, действующей на тело, к его ускорению. Вторая масса — гравитационная — определяет силу притяжения тела другими телами и его собственную силу притяжения. Вообще говоря, эти две массы измеряются, как видно из описания, в различных экспериментах, поэтому совершенно не обязаны быть пропорциональными друг другу. Их строгая пропорциональность позволяет говорить о единой массе тела как в негравитационных, так и в гравитационных взаимодействиях. Подходящим выбором единиц можно сделать эти массы равными друг другу.

Сам принцип был выдвинут ещё Исааком Ньютоном, а равенство масс было проверено им экспериментально с относительной точностью 10−3. В конце XIX века более тонкие эксперименты провёл Этвёш[8], доведя точность проверки принципа до 10−9. В течение XX века экспериментальная техника позволила подтвердить равенство масс с относительной точностью 10−12—10−13 (Брагинский, Дикке и т. д.).

Иногда принцип равенства гравитационной и инертной масс называют слабым принципом эквивалентности.

2.3 Принцип движения по геодезическим линиям

Если гравитационная масса точно равна инерционной, то в выражении для ускорения тела, на которое действуют лишь гравитационные силы, обе массы сокращаются. Поэтому ускорение тела, а следовательно, и его траектория не зависит от массы и внутреннего строения тела. Если же все тела в одной и той же точке пространства получают одинаковое ускорение, то это ускорение можно связать не со свойствами тел, а со свойствами самого пространства в этой точке.

Таким образом, описание гравитационного взаимодействия между телами можно свести к описанию пространства-времени, в котором двигаются тела. Естественно предположить, как это и сделал Эйнштейн, что тела движутся по инерции, то есть так, что их ускорение в собственной системе отсчёта равно нулю. Траектории тел тогда будут геодезическими линиями, теория которых была разработана математиками ещё в XIX веке.

Сами геодезические линии можно найти, если задать в пространстве-времени аналог расстояния между двумя событиями, называемый по традиции интервалом или мировой функцией. Интервал в трёхмерном пространстве и одномерном времени (иными словами, в четырёхмерном пространстве-времени) задаётся 10 независимыми компонентами метрического тензора. Эти 10 чисел образуют метрику пространства. Она определяет «расстояние» между двумя бесконечно близкими точками пространства-времени в различных направлениях. Геодезические линии, соответствующие мировым линиям физических тел, скорость которых меньше скорости света, оказываются линиями наибольшего собственного времени, то есть времени, измеряемого часами, жёстко скреплёнными с телом, следующим по этой траектории.

Современные эксперименты подтверждают движение тел по геодезическим линиям с той же точностью, как и равенство гравитационной и инертной масс.

2.4 Кривизна пространства-времени

Расхождение (девиация) геодезических линий вблизи массивного тела

Если запустить из двух близких точек два тела параллельно друг другу, то в гравитационном поле они постепенно начнут либо сближаться, либо удаляться друг от друга. Этот эффект называется девиацией геодезических линий. Аналогичный эффект можно наблюдать непосредственно, если запустить два шарика параллельно друг другу по резиновой мембране, на которую в центр положен массивный предмет. Шарики разойдутся: тот, который был ближе к предмету, продавливающему мембрану, будет стремиться к центру сильнее, чем более удалённый шарик. Это расхождение (девиация) обусловлено кривизной мембраны.

Аналогично, в пространстве-времени девиация геодезических линий (расхождение траекторий тел) связана с его кривизной. Кривизна пространства-времени однозначно определяется его метрикой — метрическим тензором. Различие между общей теорией относительности и альтернативными теориями гравитации определяется в большинстве случаев именно способом связи между материей (телами и полями негравитационной природы, создающими гравитационное поле) и метрическими свойствами пространства-времени.

2.5 Пространство-время ОТО и сильный принцип эквивалентности

Часто неправильно считают, что в основе общей теории относительности лежит принцип эквивалентности гравитационного и инерционного поля, который может быть сформулирован так:

Достаточно малая по размерам локальная физическая система, находящаяся в гравитационном поле, по поведению неотличима от такой же системы, находящейся в ускоренной (относительно инерциальной системы отсчёта) системе отсчёта, погружённой в плоское пространство-время специальной теории относительности.

Иногда тот же принцип постулируют как «локальную справедливость специальной теории относительности» или называют «сильным принципом эквивалентности».

Исторически этот принцип действительно сыграл большую роль в становлении общей теории относительности и использовался Эйнштейном при её разработке. Однако в самой окончательной форме теории он, на самом деле, не содержится, так как пространство-время как в ускоренной, так и в исходной системе отсчёта в специальной теории относительности является неискривленным — плоским, а в общей теории относительности оно искривляется любым телом и именно его искривление вызывает гравитационное притяжение тел.

Важно отметить, что основным отличием пространства-времени общей теории относительности от пространства-времени специальной теории относительности является его кривизна, которая выражается тензорной величиной — тензором кривизны. В пространстве-времени специальной теории относительности этот тензор тождественно равен нулю и пространство-время является плоским.

По этой причине не совсем корректным является название «общая теория относительности». Данная теория является лишь одной из ряда теорий гравитации, рассматриваемых физиками в настоящее время, в то время как специальная теория относительности (точнее, её принцип метричности пространства-времени) является общепринятой научным сообществом и составляет краеугольный камень базиса современной физики. Следует, тем не менее, отметить, что ни одна из прочих развитых теорий гравитации, кроме ОТО, не выдержала проверки временем и экспериментом.

2.6 Основные следствия ОТО

Орбита Ньютона (красная) и Эйнштейна (голубые) одной планеты вращающейся вокруг звезды

Согласно принципу соответствия, в слабых гравитационных полях предсказания общей теории относительности совпадают с результатами применения ньютоновского закона всемирного тяготения с небольшими поправками, которые растут по мере увеличения напряжённости поля.

Первыми предсказанными и проверенными экспериментальными следствиями общей теории относительности стали три классических эффекта, перечисленных ниже в хронологическом порядке их первой проверки:

1.  Дополнительный сдвиг перигелия орбиты Меркурия по сравнению с предсказаниями механики Ньютона.

2.  Отклонение светового луча в гравитационном поле Солнца.

3.  Гравитационное красное смещение, или замедление времени в гравитационном поле.

Существует ряд других эффектов, поддающихся экспериментальной проверке. Среди них можно упомянуть отклонение и запаздывание (эффект Шапиро) электромагнитных волн в гравитационном поле Солнца и Юпитера, эффект Лензе — Тирринга (прецессия гироскопа вблизи вращающегося тела), астрофизические доказательства существования чёрных дыр, доказательства излучения гравитационных волн тесными системами двойных звёзд и расширение Вселенной.

До сих пор надёжных экспериментальных свидетельств, опровергающих ОТО, не обнаружено. Отклонения измеренных величин эффектов от предсказываемых ОТО не превышают 0,01 % (для указанных выше трёх классических явлений). Несмотря на это, в связи с различными причинами теоретиками было разработано не менее 30 альтернативных теорий гравитации, причём некоторые из них позволяют получить сколь угодно близкие к ОТО результаты при соответствующих значениях входящих в теорию

3. Экспериментальные подтверждения ОТО

3.1 Эффекты, связанные с ускорением систем отсчёта

Первый из этих эффектов — гравитационное замедление времени, из-за которого любые часы будут идти тем медленнее, чем глубже в гравитационной яме (ближе к гравитирующему телу) они находятся. Данный эффект был непосредственно подтверждён в эксперименте Хафеле — Китинга, а также в эксперименте Gravity Probe A и постоянно подтверждается в GPS.

Непосредственно связанный с этим эффект — гравитационное красное смещение света. Под этим эффектом понимают уменьшение частоты света относительно локальных часов (соответственно, смещение линий спектра к красному концу спектра относительно локальных масштабов) при распространении света из гравитационной ямы наружу (из области с меньшим гравитационным потенциалом в область с большим потенциалом). Гравитационное красное смещение было обнаружено в спектрах звёзд и Солнца и надёжно подтверждено уже в контролируемых земных условиях в эксперименте Паунда — Ребки.

Гравитационное замедление времени влечёт за собой ещё один эффект, названный эффектом Шапиро (также известный как гравитационная задержка сигнала). Из-за этого эффекта в поле тяготения электромагнитные сигналы идут дольше, чем в отсутствие этого поля. Данное явление было обнаружено при радиолокации планет солнечной системы и космических кораблей, проходящих позади Солнца, а также при наблюдении сигналов от двойных пульсаров.

3.2 Гравитационное отклонение света

Самая известная ранняя проверка ОТО стала возможна благодаря полному солнечному затмению 1919 года. Артур Эддингтон показал, что свет от звезды искривлялся вблизи Солнца в точном соответствии с предсказаниями ОТО.

Искривление пути света происходит в любой ускоренной системе отсчёта. Детальный вид наблюдаемой траектории и гравитационные эффекты линзирования зависят, тем не менее, от кривизны пространства-времени. Эйнштейн узнал об этом эффекте в 1911 году, и когда он эвристическим путём вычислил величину кривизны траекторий, она оказалась такой же, какая предсказывалась классической механикой для частиц, движущихся со скоростью света. В 1916 году Эйнштейн обнаружил, что на самом деле в ОТО угловой сдвиг направления распространения света в два раза больше, чем в ньютоновской теории, в отличие от предыдущего рассмотрения. Таким образом, это предсказание стало ещё одним способом проверки ОТО.

С 1919 года данное явление было подтверждено астрономическими наблюдениями звёзд в процессе затмений Солнца, а также с высокой точностью проверено радиоинтерферометрическими наблюдениями квазаров, проходящих вблизи Солнца во время его пути по эклиптике.

Гравитационное линзирование происходит, когда один отдалённый массивный объект находится вблизи или непосредственно на линии, соединяющей наблюдателя с другим объектом, намного более удалённым. В этом случае искривление траектории света более близкой массой приводит к искажению формы удалённого объекта, которое при малом разрешении наблюдения приводит, в основном, к увеличению совокупной яркости удалённого объекта, поэтому данное явление было названо линзированием. Первым примером гравитационного линзирования было получение в 1979 году двух близких изображений одного и того же квазара QSO 0957+16 A, B (z=1,4) английскими астрономами Д. Уолшем и др. «Когда выяснилось, что оба квазара изменяют свой блеск в унисон, астрономы поняли, что в действительности это два изображения одного квазара, обязанные эффекту гравитационной линзы. Вскоре нашли и саму линзу — далёкую галактику (z=0,36), лежащую между Землей и квазаром». С тех пор было найдено много других примеров отдалённых галактик и квазаров, затрагиваемых гравитационным линзированием. Например, известен так называемый Крест Эйнштейна, когда галактика учетверяет изображение далёкого квазара в виде креста.

Специальный тип гравитационного линзирования называется кольцом или дугой Эйнштейна. Кольцо Эйнштейна возникает, когда наблюдаемый объект находится непосредственно позади другого объекта со сферически-симметричным полем тяготения. В этом случае свет от более отдалённого объекта наблюдается как кольцо вокруг более близкого объекта. Если удалённый объект будет немного смещён в одну сторону и/или поле тяготения не сферически-симметричное, то вместо этого появятся частичные кольца, называемые дугами.

Наконец, у любой звезды может увеличиваться яркость, когда перед ней проходит компактный массивный объект. В этом случае увеличенные и искажённые из-за гравитационного отклонения света изображения дальней звезды не могут быть разрешены (они находятся слишком близко друг к другу) и наблюдается просто повышение яркости звезды. Этот эффект называют микролинзированием, и он наблюдается теперь регулярно в рамках проектов, изучающих невидимые тела нашей Галактики по гравитационному микролинзированию света от звёзд — МАСНО, EROS (англ.) и другие.

3.3 Чёрные дыры

Чёрная дыра — область, ограниченная так называемым горизонтом событий, которую не может покинуть ни материя, ни информация. Предполагается, что такие области могут образовываться, в частности, как результат коллапса массивных звёзд. Поскольку материя может попадать в чёрную дыру (например, из межзвёздной среды), но не может её покидать, масса чёрной дыры со временем может только возрастать.

Стивен Хокинг, тем не менее, показал, что чёрные дыры могут терять массу за счёт излучения, названного излучением Хокинга. Излучение Хокинга представляет собой квантовый эффект, который не нарушает классическую ОТО.

Известно много кандидатов в чёрные дыры, в частности супермассивный объект, связанный с радиоисточником Стрелец A* в центре нашей Галактики. Подавляющее большинство учёных убеждены, что наблюдаемые астрономические явления, связанные с этим и другими подобными объектами, надёжно подтверждают существование чёрных дыр, однако существуют и другие объяснения: например, вместо чёрных дыр предлагаются бозонные звёзды и другие экзотические объекты.

3.4 Орбитальные эффекты

ОТО корректирует предсказания ньютоновской теории небесной механики относительно динамики гравитационно связанных систем: Солнечная система, двойные звёзды и т. д.

Первый эффект ОТО заключался в том, что перигелии всех планетных орбит будут прецессировать, поскольку гравитационный потенциал Ньютона будет иметь малую релятивистскую добавку, приводящую к формированию незамкнутых орбит. Это предсказание было первым подтверждением ОТО, поскольку величина прецессии, выведенная Эйнштейном в 1916 году, полностью совпала с аномальной прецессией перигелия Меркурия. Таким образом была решена известная в то время проблема небесной механики.

Позже релятивистская прецессия перигелия наблюдалась также у Венеры, Земли, астероида Икар и как более сильный эффект в системах двойных пульсаров. За открытие и исследования первого двойного пульсара PSR B1913+16 в 1974 году Р. Халс и Д. Тейлор получили Нобелевскую премию в 1993 году.

Другой эффект — изменение орбиты, связанное с гравитационным излучением двойной и более кратной системы тел. Этот эффект наблюдается в системах с близко расположенными звёздами и заключается в уменьшении периода обращения. Он играет важную роль в эволюции близких двойных и кратных звёзд. Эффект впервые наблюдался в вышеупомянутой системе PSR B1913+16 и с точностью до 0,2 % совпал с предсказаниями ОТО.

Ещё один эффект — геодезическая прецессия. Она представляет собой прецессию полюсов вращающегося объекта в силу эффектов параллельного перенесения в искривлённом пространстве-времени. Данный эффект отсутствует в ньютоновской теории тяготения. Предсказание геодезической прецессии было проверено в эксперименте с зондом НАСА «Грэвити Проуб Би» (Gravity Probe B). Руководитель исследований данных, полученных зондом, Фрэнсис Эверитт на пленарном заседании Американского физического общества 14 апреля 2007 года заявил о том, что анализ данных гироскопов позволил подтвердить предсказанную Эйнштейном геодезическую прецессию с точностью, превосходящей 1 %.

3.5 Увлечение инерциальных систем отсчёта

Увлечение инерциальных систем отсчёта вращающимся телом заключается в том, что вращающийся массивный объект «тянет» пространство-время в направлении своего вращения: удалённый наблюдатель в покое относительно центра масс вращающегося тела обнаружит, что самыми быстрыми часами (то есть покоящимися относительно локально-инерциальной системы отсчёта) на фиксированном расстоянии от объекта являются часы, имеющие компоненту движения вокруг вращающегося объекта в направлении вращения, а не те, которые находятся в покое относительно наблюдателя, как это происходит для невращающегося массивного объекта. Точно так же удалённым наблюдателем будет установлено, что свет двигается быстрее в направлении вращения объекта, чем против его вращения. Увлечение инерциальных систем отсчёта также вызовет изменение ориентации гироскопа во времени. Для космического корабля на полярной орбите направление этого эффекта перпендикулярно геодезической прецессии, упомянутой выше.

Поскольку эффект увлечения инерциальных систем отсчёта в 170 раз слабее эффекта геодезической прецессии, стэнфордские учёные пока по-прежнему извлекают его «отпечатки» из информации, полученной зондом «Грэвити Проуб Би» (Gravity Probe B).

3.6 Другие предсказания

Эквивалентность инерционной и гравитационной массы: следствие того, что свободное падение — движение по инерции. Принцип эквивалентности: даже самогравитирующий объект отзовётся на внешнее поле тяготения в той же мере, что и тестовая частица.

Гравитационное излучение: вращение двойных звёзд и планет, а также процессы слияния нейтронных звёзд и/или чёрных дыр, как ожидается, должны сопровождаться излучением гравитационых волн.

Слияние двойных пульсаров может создавать гравитационные волны, достаточно сильные, чтобы наблюдаться на Земле. На 2009 год существуют (или будут в ближайшее время построены) несколько гравитационных телескопов для наблюдения подобных волн, однако пока имеются лишь косвенные доказательства существования гравитационного излучения в виде измерений темпа потери энергии вращения тесными двойными звёздами.

Гравитоны. Согласно квантовой механике, гравитационное излучение должно быть составлено из квантов, названных гравитонами. ОТО предсказывает, что они будут безмассовыми частицами со спином, равным 2. Обнаружение отдельных гравитонов в экспериментах связано со значительными проблемами, так что существование квантов гравитационного поля до сих пор (2009 год) не показано.

4. Космология

Хотя общая теория относительности была создана как теория тяготения, скоро стало ясно, что эту теорию можно использовать для моделирования Вселенной как целого, и так появилась физическая космология. Центральным пунктом для физической космологии является метрика Фридмана — Леметра — Робертсона — Уокера, которая является космологическим решением уравнений Эйнштейна. Это решение предсказывает, что Вселенная должна быть динамической: она должна расширяться, сжиматься или совершать постоянные колебания.

Эйнштейн сначала не мог примириться с идеей динамической Вселенной, хотя она явно следовала из уравнений Эйнштейна без космологического члена. Поэтому в попытке переформулировать ОТО так, чтобы решения описывали статичную Вселенную, Эйнштейн добавил космологическую постоянную к полевым уравнениям (см. выше). Однако получившаяся статическая вселенная была нестабильна. Позднее в 1929 году Эдвин Хаббл показал, что красное смещение света от отдалённых галактик указывает, что они удаляются от нашей собственной галактики со скоростью, которая пропорциональна их расстоянию от нас. Это продемонстрировало, что вселенная действительно не статична и расширяется. Открытие Хаббла показало несостоятельность воззрений Эйнштейна и использования им космологической постоянной. Теория нестационарной Вселенной (включая учёт космологического члена) была создана, впрочем, ещё до открытия закона Хаббла усилиями Фридмана, Леметра и ДеСиттера.

Уравнения, описывающие расширение Вселенной, показывают, что она становится сингулярной, если вернуться назад во времени достаточно далеко. Это событие называют Большим Взрывом. В 1948 году Дж. Гамов издал статью, описывающую процессы в ранней Вселенной в предположении её высокой температуры и предсказывающую существование космического микроволнового фонового излучения, происходящего от горячей плазмы Большого Взрыва; в 1949 году Р. Алфер и Герман провели более подробные вычисления. В 1965 году А. Пензиас и Р. Вилсон впервые идентифицировали реликтовое излучение, подтвердив таким образом теорию Большого Взрыва и горячей ранней Вселенной.

5. Проблемы ОТО

5.1 Проблема энергии

Так как энергия, с точки зрения математической физики, представляет собой величину, сохраняющуюся из-за однородности времени[53], а в общей теории относительности, в отличие от специальной, вообще говоря, время неоднородно[~ 4], то закон сохранения энергии может быть выражен в ОТО только локально, то есть в ОТО не существует такой величины, эквивалентной энергии в СТО, чтобы интеграл от неё по пространству сохранялся при движении по времени. Локальный же закон сохранения энергии-импульса в ОТО существует и является следствием уравнений Эйнштейна:

где точка с запятой обозначает взятие ковариантной производной. Переход от него к глобальному закону невозможен, потому что так интегрировать тензорные поля, кроме скалярных, в римановом пространстве, чтобы получать тензорные (инвариантные) результаты, вообще говоря, математически невозможно.

Многие физики считают это существенным недостатком ОТО. С другой стороны, очевидно, что если соблюдать последовательность до конца, в полную энергию, кроме энергии материи, необходимо включать также и энергию самого гравитационного поля. А последняя не может быть хорошо определена (как тензор), что является ещё одним аспектом проблемы. Различными авторами вводятся так называемые псевдотензоры энергии-импульса гравитационного поля, которые обладают некими «правильными» свойствами, но одно их многообразие показывает, что удовлетворительного решения задача не имеет. В общем случае проблема энергии и импульса может считаться решённой только для островных систем, то есть таких распределений массы, которые ограничены в пространстве, и пространство-время которых на пространственной бесконечности переходит в пространство Минковского. Тогда, выделяя группу асимптотической симметрии пространства-времени (группу Бонди — Сакса), можно определить 4-векторную величину энергии-импульса системы, правильно ведущую себя относительно преобразований Лоренца на бесконечности.

Существует необщепринятая точка зрения, восходящая к Лоренцу и Леви-Чивита, которая определяет тензор энергии-импульса гравитационного поля как тензор Эйнштейна с точностью до постоянного множителя. Тогда уравнения Эйнштейна утверждают, что энергия-импульс гравитационного поля в любом объёме точно уравновешивает энергию-импульс материи в этом объёме, так что полная их сумма всегда тождественно равна нулю[55].

5.2 ОТО и квантовая физика

Главной проблемой ОТО с современной точки зрения является невозможность построения для неё квантово-полевой модели каноническим образом. Каноническое квантование любой физической модели состоит в том, что в неквантовой модели строятся уравнения Эйлера — Лагранжа и определяется лагранжиан системы, из которого выделяется гамильтониан H. Затем гамильтониан переводят из обычной функции динамических переменных системы в операторную функцию соответствующих динамическим переменным операторов — квантуют. При этом физический смысл оператора Гамильтона состоит в том, что его собственные значения представляют собой уровни энергии системы. Ключевая особенность описанной процедуры состоит в том, что она предполагает выделение параметра — времени, по которому и составляется, в дальнейшем, уравнение типа Шрёдингера

здесь  — уже квантовый гамильтониан, которое далее решается для отыскания волновой функции .

Сложности в реализации такой программы для ОТО троякие: во-первых, переход от классического гамильтониана к квантовому неоднозначен, так как операторы динамических переменных не коммутируют между собой; во-вторых, гравитационное поле относится к типу полей со связями, для которых структура уже классического фазового пространства достаточно сложна, а квантование их наиболее прямым методом невозможно; в-третьих, в ОТО нет выраженного направления времени, что составляет трудность при его необходимом выделении и порождает проблему интерпретации полученного решения.

Тем не менее, программа квантования гравитационного поля была успешно решена к 50-м годам XX столетия усилиями М. П. Бронштейна, П. А. М. Дирака, Брайса Девитта и других физиков. Оказалось, что (по крайней мере слабое) гравитационное поле можно рассматривать как квантовое безмассовое поле спина 2.

Дополнительные сложности возникли при попытке вторичного квантования системы гравитационного поля, проведённой Р. Фейнманом, Брайсом Девиттом и другими физиками в 1960-х годах после разработки квантовой электродинамики. Оказалось, что поле такого высокого спина в трёхмерном пространстве не перенормируемо никакими традиционными (и даже нетрадиционными) способами. Более того, не существует никакого разумного определения его энергии, такого, чтобы выполнялся закон сохранения энергии, она была бы локализуема и неотрицательна в любой точке.

Полученный тогда результат остаётся незыблемым до настоящего времени. Расходимости в квантовой гравитации, появляющиеся в каждом новом порядке по количеству петель, невозможно сократить введением в гамильтониан никакого конечного количества перенормировочных контрчленов. Невозможно и свести перенормировку к конечному числу постоянных величин (как это удалось сделать в квантовой электродинамике по отношению к элементарному электрическому заряду и массе заряженной частицы).

На сегодняшний день построено много теорий, альтернативных ОТО (теория струн, получившая развитие в М-теории, петлевая квантовая гравитация и другие), которые позволяют квантовать гравитацию, но все они либо не закончены, либо имеют внутри себя неразрешённые парадоксы. Также подавляющее большинство из них обладает огромным недостатком, который вообще не даёт возможности говорить о них как о «физических теориях», — они не могут быть проверены экспериментально.

6. Специальная теория относительности (СТО)

Специа́льная тео́рия относи́тельности (СТО) — теория, описывающая движение, законы механики и пространственно-временные отношения, определяющие их, при скоростях движения, близких к скорости света. В рамках специальной теории относительности классическая механика Ньютона является приближением низких скоростей. Обобщение СТО для гравитационных полей образует общую теорию относительности.

6.1 Создание СТО

Предпосылкой к созданию теории относительности явилось развитие в XIX веке электродинамики. Результатом обобщения и теоретического осмысления экспериментальных фактов и закономерностей в областях электричества и магнетизма стали уравнения Максвелла, описывающие эволюцию электромагнитного поля и его взаимодействие с зарядами и токами.

Другим следствием развития электродинамики стал переход от ньютоновской концепции дальнодействия, согласно которой взаимодействующие на расстоянии тела воздействуют друг на друга через пустоту, причём взаимодействие осуществляется с бесконечной скоростью, то есть «мгновенно», к концепции близкодействия, предложенной Майклом Фарадеем, в которой взаимодействие передаётся с помощью промежуточных агентов — полей, заполняющих пространство — и при этом встал вопрос о скоростях распространения как взаимодействий, переносимых полями, так и самих полей. Скорость распространения электромагнитного поля в пустоте вытекала из уравнений Максвелла и оказалась постоянной и равной скорости света.

Однако в связи с этим встал вопрос — относительно чего постоянна скорость света? В максвелловской электродинамике скорость распространения электромагнитных волн оказалась не зависящей от скоростей движения как источника этих волн, так и наблюдателя. Аналогичной оказалась и ситуация с магнитостатическими решениями, вытекающими из уравнений Максвелла: статические магнитные поля и силы Лоренца, действующие на движущиеся в магнитных полях заряды, зависят от скоростей зарядов по отношению к наблюдателю, то есть уравнения Максвелла оказались неинвариантными относительно принципа относительности и преобразований Галилея — что противоречило ньютоновской концепции абсолютного пространства классической механики.

Специальная теория относительности была разработана в начале XX века усилиями Г. А. Лоренца, А. Пуанкаре и А. Эйнштейна, см. ниже исторический очерк. Экспериментальной основой для создания СТО послужил опыт Майкельсона, который дал результат измерения, неожиданный для классической физики своего времени: независимость скорости света от системы отсчёта. Попытка проинтерпретировать этот результат в начале XX века вылилась в пересмотр классических представлений не только электромагнетизма, но и всей механики вообще, и привела к созданию релятивистских физических теорий.

7. Постулаты Эйнштейна

СТО полностью выводится на физическом уровне строгости из трёх постулатов (предположений):

1.  Справедлив принцип относительности Эйнштейна — расширение принципа относительности Галилея.

2.  Скорость света не зависит от скорости движения источника во всех инерциальных системах отсчёта.

3.  Пространство и время - однородны, пространство является изотропным.

Формулировка второго постулата может быть шире: «Скорость света постоянна во всех инерциальных системах отсчёта», но для вывода СТО достаточно его исходной формулировки Эйнштейном, записанной выше. Третий постулат в явном виде обычно не фигурирует в вариантах вывода СТО, но подразумевается. Приписывание постулатов Эйнштейну правомерно в той степени, что до его работы эти уже сформулированные отдельно друг от друга (в частности, А. Пуанкаре) утверждения в совокупности явным образом никем не рассматривались.

Иногда в постулаты СТО также добавляют условие синхронизации часов по А. Эйнштейну, но принципиального значения оно не имеет: при других условиях синхронизации лишь усложняется математическое описание экспериментальной ситуации без изменения предсказываемых и измеряемых эффектов (см. по этому поводу работы в списке литературы).

Тем не менее, опора на достижения экспериментальной физики позволяет утверждать, что в пределах своей области применимости — при пренебрежении эффектами гравитационного взаимодействия тел — СТО является справедливой с очень высокой степенью точности (до 10−12 и выше). По меткому замечанию Л. Пэйджа, «в наш век электричества вращающийся якорь каждого генератора и каждого электромотора неустанно провозглашает справедливость теории относительности — нужно лишь уметь слушать».

8. Сущность СТО

Следствием постулатов СТО являются преобразования Лоренца, заменяющие собой преобразования Галилея для нерелятивистского, «классического» движения. Эти преобразования связывают между собой координаты и времена одних и тех же событий, наблюдаемых из различных инерциальных систем отсчёта.

При движении с околосветовыми скоростями видоизменяются также и законы динамики. Так, можно вывести, что второй закон Ньютона, связывающий силу и ускорение, должен быть модифицирован при скоростях тел, близких к скорости света. Кроме того, можно показать, что и выражение для импульса и кинетической энергии тела уже имеет более сложную зависимость от скорости, чем в нерелятивистском случае.

Специальная теория относительности получила многочисленные подтверждения на опыте и является безусловно верной теорией в своей области применимости.

8.1 Четырёхмерный континуум — пространство-время

С математической точки зрения, непривычные свойства СТО можно интерпретировать как результат того, что время и пространство не являются независимыми понятиями, а образуют пространство-время Минковского, которое является псевдоевклидовым пространством. Вращения базиса в этом четырёхмерном пространстве-времени, смешивающие временную и пространственные координаты 4-векторов, выглядят для нас как переход в движущуюся систему отсчета и похожи на вращения в обычном трёхмерном пространстве. При этом естественно изменяются проекции четырёхмерных интервалов между определёнными событиями на временную и пространственные оси системы отсчёта, что и порождает релятивистские эффекты изменения временных и пространственных интервалов. Именно инвариантная структура этого пространства, задаваемая постулатами СТО, не меняется при переходах от одного условия синхронизации часов к другому, и гарантирует независимость результатов экспериментов от принятого условия.

Аналог расстояния между событиями в пространстве Минковского, называемый интервалом, при введении наиболее простых координат, аналогичных декартовым координатам трёхмерного пространства, даётся выражением:

Обратите внимание: «квадрат расстояния» между двумя разными событиями может быть не только положительным, но и отрицательным и даже нулём. Именно незнакоопределённость метрики определяет свойства пространства-времени, делая его геометрию псевдоевклидовой.

9. Отношения теории относительности с другими физическими понятиями

9.1 Гравитация

Для описания гравитации разработано особое расширение теории относительности, в котором допускается кривизна пространства-времени. Тем не менее, динамика даже в рамках СТО может включать гравитационное взаимодействие, пока потенциал гравитационного поля много меньше c2.

Следует также заметить, что специальная теория относительности перестает работать в масштабах всей Вселенной, требуя замены на ОТО.

9.2 Классическая механика

Теория относительности входит в существенное противоречие с некоторыми аспектами классической механики. Например, парадокс Эренфеста показывает несовместимость СТО с понятием абсолютно твёрдого тела. Надо отметить, что даже в классической физике предполагается, что механическое воздействие на твёрдое тело распространяется со скоростью звука, а отнюдь не с бесконечной (как должно быть в воображаемой абсолютно твёрдой среде).

9.3 Квантовая механика

Специальная теория относительности (в отличие от общей) полностью совместима с квантовой механикой. Их синтезом является квантовая теория поля. Более того, такое квантово-механическое явление как спин без привлечения теории относительности не имеет разумного объяснения. Однако, обе теории вполне независимы друг от друга. Возможно построение как квантовой механики, основанной на нерелятивистском принципе относительности Галилея, так и теорий на основе СТО, полностью игнорирующих квантовые эффекты.

Развитие квантовой теории всё ещё продолжается, и многие физики считают, что будущая полная теория ответит на все вопросы, имеющие физический смысл, и даст в пределах как СТО в сочетании с квантовой теорией поля, так и ОТО. Скорее всего СТО ожидает такая же судьба, как и механику Ньютона — будут точно очерчены пределы её применимости. В то же время такая максимально общая теория пока является очень отдалённой перспективой.

10. Эффекты СТО

Пусть система отсчёта K' движется со скоростью V относительно системы отсчёта K0, соответственно, штрихованные величины относятся к K', а величины с индексом 0 — к K0. К наиболее распространённым эффектам СТО, также называемым релятивистскими эффектами, относят:

10.1 Замедление времени

Время в движущейся системе отсчёта течёт медленнее:

С этим эффектом связан так называемый парадокс близнецов.

Парадокс близнецов — мысленный эксперимент с двумя близнецами N и N`, движущимися относительно друг друга. Согласно эффекту релятивистского замедления времени каждый из близнецов считает (и это подтверждается его наблюдениями), что часы другого близнеца идут медленнее, чем его часы.

Если один из близнецов улетит, а потом вернётся, то кто из них окажется младше?

Согласно СТО младше окажется улетавший и вернувшийся.

Возникает парадокс: Почему, если каждый видел, что время замедляется у другого, младше становится именно улетавший?

Близнец, который вернулся, неизбежно должен был изменить свою скорость. Поэтому его система отсчёта не является инерциальной (он должен двигаться с ускорением). А согласно СТО равноправны только инерциальные системы. Следовательно, нет ничего удивительного, что системы оказываются несимметричными.

Парадоксом близнецов часто называют сам вывод теории относительности о том, что один из близнецов состарится сильнее другого. Хотя такая ситуация и необычна, в ней нет внутреннего противоречия, а многочисленные эксперименты по релятивистскому замедлению времени подтверждают теорию относительности и дают основание утверждать, что так и будет на самом деле.

10.2 Сокращение линейных размеров

Линейные размеры тел в движущейся системе отсчёта сокращаются.

Парадокса шеста и сарая:

Из СТО мы знаем, что движущиеся тела сокращаются в направлении движения. Возьмём сарай с двумя сквозными дверьми. Возьмём шест, который чуть длиннее, чем сарай. Если открыть обе двери и просунуть в них шест, то он в сарай не поместится и будет торчать из дверей по обе стороны. Воспользуемся сокращением длин — разгоним шест до такой скорости, чтобы он сократился, допустим в два раза, и тогда, пролетая сквозь сарай, он весь целиком там поместится! Захлопнем двери сарая, пока шест находится внутри и тут же быстренько их откроем, чтобы не поломать шест. И мы видим следующее противоречие: система отсчёта, связанная с шестом, такая же равноправная, как и связанная с сараем. То есть, в ней будут наблюдаться те же эффекты сокращения продольных размеров, но только уже сарая! В ней сарай станет короче, и чуть более длинный изначально шест станет еще более длинным и никогда в сарай не поместится. Значит, захлопнув двери сарая, мы обязательно сломаем шест!

Этот парадокс — один из типичных случаев, когда, вцепившись в один из эффектов СТО, человек делает далеко идущие выводы, пренебрегая другими, подчас более важными, эффектами. Сокращение длин действительно произойдет так, как описано в парадоксе — для сарая шест окажется укороченным и поместится в нём целиком, а для шеста — сарай окажется укороченным и не сможет поместить в себя весь шест. Так где же правда?

А правда — в относительности одновременности. Сокращение длин — это второстепенный эффект, относительность же одновременности — намного же более важный. Ещё раз вспомним уже сказанное тут: события, одновременные в одной системе отсчета, будут по СТО неодновременными в другой системе отсчёта, если системы движутся друг относительно друга. Если присмотреться к эксперименту, у нас в нём есть чётко выраженные события, одновременные в ИСО сарая — это момент, когда мы закрываем переднюю и заднюю двери сарая. Мы делаем это в ИСО сарая ОДНОВРЕМЕННО. Нетрудно догадаться, что в ИСО шеста они произойдут в разные моменты времени, а именно: когда передний конец шеста войдет в сарай и приблизится к задней двери, она захлопнется и тут же откроется, а когда задний конец шеста сравняется с передней дверью, захлопнется и откроется, в свою очередь, и она. Таким образом, шест не сломается ни в ИСО сарая, ни в ИСО шеста. Если внимательно присмотреться к этому парадоксу, то можно сделать один важный вывод насчёт эффекта сокращения длин. Как мы измеряем длину объекта? Прикладываем к нему линейку и смотрим на показания шкалы у начала и конца объекта. А что если этот объект двигается? Тогда, чтобы не испортить показания, посмотреть на шкалу у начала и конца объекта надо одновременно, а иначе показания окажутся неверными. Но ведь то, что в нашей ИСО по теории относительности одновременно, в другой ИСО будет неодновременным.

Парадокс диска:

Рассмотрим велосипедное колесо, которое крутится с большой скоростью. Каждый элемент спицы движется перпендикулярно своей длине и сокращения в продольном измерении не испытывает. Значит, не испытывает сокращения и вся спица. С другой стороны, каждый элемент обода движется вдоль своей длины и сокращается. Таким образом, отношение длины окружности к её радиусу меняется.

Разгадка в том, что каждый элемент колеса движется ускоренно, и СТО тут малоприменимо. В ОТО же непостоянность числа π совершенно нормальна.

10.3 О релятивистской массе

Так называемая релятивистская масса движущегося объекта определяется соотношением (верным и для частиц, движущихся со скоростью света):

Релятивистская масса движущегося объекта больше массы покоя:

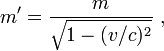
и возрастает с увеличением скорости. «Утяжеление» следует понимать лишь условно, так как второй закон Ньютона в форме F = m'a всё равно не выполняется (направление ускорения в общем случае не совпадает с направлением силы).

В современной физической литературе по СТО, однако, принято, что m — масса частицы (инвариантная масса) не зависит от скорости, являясь инвариантом относительно преобразований Лоренца, и является величиной неаддитивной. Понятие «релятивистской массы» не используется и не рекомендуется к применению, хотя оно и встречается в ранних работах по теории относительности.

11. Исторический очерк

В 1728 году английский астроном Брэдли открыл аберрацию света: все звёзды описывают на небосводе малые круги с периодом в один год. С точки зрения эфирной теории света это означало, что эфир неподвижен, и его кажущееся смещение (при движении Земли вокруг Солнца) по принципу суперпозиции отклоняет изображения звёзд. Френель, однако, допускал, что внутри вещества эфир частично увлекается. Эта точка зрения, казалось, нашла подтверждение в опытах Физо, который обнаружил, что скорость света в воде зависит от направления её движения: вдоль течения скорость света больше, чем против течения.

Максвелл в 1868 году предложил схему решающего опыта, который после изобретения интерферометра смог осуществить в 1881 году американский физик Майкельсон. Позже Майкельсон и Эдуард Морли повторили опыт несколько раз с возрастающей точностью, но результат был неизменно отрицательным — «эфирного ветра» не существовало.

В 1892 году Лоренц и (независимо от него) Джордж Фитцджеральд предположили, что эфир неподвижен, а длина любого тела сокращается в направлении его движения. Одновременно изучался вопрос, при каких преобразованиях координат уравнения Максвелла инвариантны. Правильные формулы впервые выписали Лармор (1900) и Пуанкаре (1905), последний доказал их групповые свойства и предложил назвать преобразованиями Лоренца.

Пуанкаре также дал обобщённую формулировку принципа относительности, охватывающего и электродинамику. Тем не менее он продолжал признавать эфир, хотя придерживался мнения, что его никогда не удастся обнаружить — см. доклад Пуанкаре на физическом конгрессе, 1900 год[2]. В этом же докладе Пуанкаре впервые высказывает мысль, что одновременность событий не абсолютна, а представляет собой условное соглашение («конвенцию»). Было высказано также предположение о предельности скорости света.

Под влиянием критики Пуанкаре Лоренц в 1904 году предложил новый вариант своей теории. В ней он предположил, что при больших скоростях механика Ньютона нуждается в поправках. В 1905 году Пуанкаре далеко развил эти идеи в статье «О динамике электрона». Предварительный вариант статьи появился в 1895 году в Comptes Rendus, развёрнутый был закончен в июле 1905 года, опубликован в январе 1906 года, почему-то в малоизвестном итальянском математическом журнале.

В этой итоговой статье формулируется всеобщий принцип относительности с преобразованиями Лоренца для всех явлений (не только электромагнитных). Пуанкаре нашёл выражение для четырёхмерного интервала как инварианта преобразований Лоренца: r2 + (ict)2. Он даже предложил нечто вроде релятивистского обобщения теории гравитации; в его теории тяготение распространялось в эфире со скоростью света.

Таким образом, в начале XX века существовали две несовместимые кинематики: классическая, с преобразованиями Галилея, и электромагнитная, с преобразованиями Лоренца. Эйнштейн, размышляя на эти темы, предположил, что первая есть приближённый случай второй для малых скоростей, а то, что считалось свойствами эфира, есть на деле проявление объективных свойств пространства и времени. Эйнштейн пришёл к выводу, что нелепо привлекать понятие эфира только для того, чтобы доказать невозможность его наблюдения. В своей основополагающей статье «К электродинамике движущихся сред» (1905) он предложил два постулата: специальный принцип относительности и постоянство скорости света; из них без труда выводятся лоренцево сокращение, формулы преобразования Лоренца, относительность одновременности, ненужность эфира, новая формула суммирования скоростей, возрастание инерции со скоростью и т. д. В последующих работах появилась и формула E0 = mc2 — масса определяется энергией покоя.

Часть учёных сразу приняли СТО: Планк (1906) и сам Эйнштейн (1907) построили релятивистскую динамику и термодинамику. Минковский в 1907 году представил математическую модель кинематики СТО, в которой преобразования Лоренца вытекают из геометрии четырёхмерного псевдоевклидова пространства: в пространстве Минковского, лоренцевы преобразования являются преобразованиями поворотов координатных осей.

Были, однако, и критики новых концепций. Они указывали на то, что теория относительности не предсказывает новых фактов, которые можно проверить экспериментально, и ничем не лучше теории Лоренца. Появились попытки найти в СТО внутренние противоречия. Концепцию эфира продолжали поддерживать Дж. Дж. Томсон, Ленард, Лодж и другие известные физики. Сам Лоренц прекратил критику СТО только к концу жизни; свои разногласия с теорией относительности он сам сформулировал так:

Основная причина, по которой я не смог предложить теории относительности, заключается в том, что я придерживался представления, будто лишь переменная t может считаться истинным временем, а предложенное мной местное время t' должно рассматриваться только в качестве вспомогательной математической величины.

С 1911 года Эйнштейн разрабатывал общую теорию относительности (ОТО), включающую гравитацию, на основе принципа эквивалентности, которую завершил в 1916 году.

В 1930-е годы был проведен ряд экспериментов для проверки главного постулата СТО — постоянства скорости света. Некоторые измерения (Миллер и др.) поставили его под сомнение, однако точные эксперименты Мак-Кеннеди подтвердили этот факт. Постепенно накапливались опытные подтверждения СТО. На ней основаны квантовая теория поля, теория ускорителей, она учитывается при проектировании и работе спутниковых систем навигации (здесь оказались нужны даже поправки общей теории относительности) и др.

Ряд экспериментов по проверке эффектов СТО и ОТО был проведен в конце XX века; их результаты находятся в полном согласии с теорией. Тем не менее исследования с целью найти границы применимости теории относительности продолжаются.

12. Заключение

Общая теория относительности, в настоящее время — самая успешная теория, хорошо подтверждённая наблюдениями. Первый успех общей теории относительности состоял в объяснении аномальной прецессии перигелия Меркурия. Затем, в 1919 году, Артур Эддингтон сообщил о наблюдении отклонения света вблизи Солнца в момент полного затмения, что качественно и количественно подтвердило предсказания общей теории относительности. С тех пор многие другие наблюдения и эксперименты подтвердили значительное количество предсказаний теории, включая гравитационное замедление времени, гравитационное красное смещение, задержку сигнала в гравитационном поле и, пока лишь косвенно, гравитационное излучение. Кроме того, многочисленные наблюдения интерпретируются как подтверждения одного из самых таинственных и экзотических предсказаний общей теории относительности — существования чёрных дыр

Так же, как и в случае квантовой механики, многие предсказания теории относительности противоречат интуиции, кажутся невероятными и невозможными. Это, однако, не означает, что теория относительности неверна. В действительности, то, как мы видим (либо хотим видеть) окружающий нас мир и то, каким он является на самом деле, может сильно различаться. Уже больше века учёные всего мира пробуют опровергнуть СТО. Ни одна из этих попыток не смогла найти ни малейшего изъяна в теории. О том, что теория верна математически, свидетельствует строгая математическая форма и чёткость всех формулировок.

О том, что СТО действительно описывает наш мир, свидетельствует огромный экспериментальный опыт. Многие следствия этой теории используются на практике. Очевидно, что все попытки «опровергнуть СТО» обречены на провал потому, что сама теория опирается на три постулата Галилея (которые несколько расширены), на основе которых построена ньютонова механика, а также на дополнительный постулат о постоянстве скорости света во всех системах отсчета. Все четыре не вызывают какого-либо сомнения в пределах максимальной точности современных измерений: лучше 10 − 12, а в некоторых аспектах — до 10 − 15. Более того, точность их проверки является настолько высокой, что постоянство скорости света положено в основание определения метра — единицы длины, в результате чего скорость света становится константой автоматически.

13. Список литературы

·  Ландау, Л. Д., Лифшиц, Е. М. Теория поля. — Издание 7-е, исправленное. — М.: Наука, 1988. — 512 с. — («Теоретическая физика», том II). — ISBN 5-02-014420-7

·  Паули В. Теория относительности. Изд. 2-е, испр. и доп. Перев. с нем. — М.: Наука, 1983. — 336 с.

·  Спасский Б. И.. История физики. Том 2, часть 2-я. М.: Высшая школа, 1977.

·  Эйнштейн А. Сущность теории относительности. — М.: Изд. ин. лит., 1955. — 157 с.

·  Уиттекер Э. История теории эфира и электричества. Современные теории 1900-1926. Пер с англ. Москва, Ижевск: ИКИ, 2004. 464с. ISBN 5-93972-304-7 (Глава 2)

·  Визгин В. П. Релятивистская теория тяготения (истоки и формирование, 1900–1915). М.: Наука, 1981. - 352c.

·  Герман Вейль. Пространство. Время. Материя. Лекции по общей теории относительности. — М.: Изд-во УРСС научной и учебной литературы, 2004. 455 с.

·  Дирак П. А. М. Общая теория относительности М.: Атомиздат, 1978.

·  Фок В. А. Теория пространства, времени и тяготения / 2-е изд. М.: ГИФМЛ, 1961.

·  Толмен Р. Относительность, термодинамика и космология М.: Наука, 1974.

·  Пенроуз Р. Структура пространства-времени М.: Мир, 1972.

·  Мизнер Ч., Торн К., Уилер Дж. Гравитация. М.: Мир, 1977. Том 1 Том 2 Том 3

·  Хокинг С., Эллис Дж. Крупномасштабная структура пространства-времени М.: Мир, 1977.

·  Визгин В. П. Релятивистская теория тяготения (истоки и формирование, 1900—1915). М.: Наука, 1981. — 352 c.

·  Визгин В. П. Единые теории в 1-й трети ХХ в. М.: Наука, 1985. — 304 c.

·  http://www.wikipedia.ru

·  http://www.lurkmore.ru