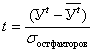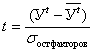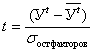Курсовая работа: Статистическая обработка земельно-кадастровой информации

МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА рОССИЙСКОЙ ФЕДЕРАЦИИ

Государственный университет по землеустройству

Кафедра землепользования и земельного кадастра

Расчетно-графическая работа

Статистическая обработка

земельно-кадастровой информации

Выполнил ст. 41к (1) гр. Белов В.С.

Проверил Валиев Д. С.

Москва 2003

СОДЕРЖАНИЕ

ВВЕДЕНИЕ……………………………………………………..……………………….3

ГЛАВА 1. Анализ и выравнивание динамических рядов

1. 1. Анализ динамических рядов………………………………..……………..4

1. 2. Выравнивание динамических рядов………………………...…………….7

ГЛАВА 2. Вариационные ряды

2. 1. Построение и анализ вариационных рядов………………….…………..17

2. 2. Статистическая группировка земельно-кадастровых показателей

и построение статистических таблиц………………………………...…24

ГЛАВА 3. Математическая обработка исходной информации

3. 1. Определение тесноты связи между результатирующим фактором

и факторами, влияющими на него, а также тесноты связи между

самими влияющими факторами……………………………………….…38

3. 2. Графическое отображение связи между результирующим фактором

и фактором, в наибольшей степени на него влияющим………………..42

ВВЕДЕНИЕ

Земельно-кадастровые работы связаны с большим объемом информации, где не существует функциональной зависимости между варьирующими факторами. Исследования в земельном кадастре не могут успешно развиваться без математической обработки материалов о природных свойствах почв, интенсивности ведения земледелия и плодородия сельскохозяйственных культур. В частности научной основой бонитировки почв являются достоверные данные о свойствах почв, коррелирующие с урожайностью сельскохозяйственных культур.

Статистика определяется как собирание, представление, анализ и интерпретация числовых данных. Собирание информации происходит с помощью наблюдений, представление – с помощью группировок, обобщения сводок. Информация представляется в виде таблиц. Анализ – это нахождение взаимосвязей между явлениями, интерпретация заключается в выражении статистических зависимостей, закономерностей. Предметом статистического изучения выступают совокупности – множества одно-качественных варьирующих явлений, т. е. множества явлений, объединенных общим качеством, представляющих собой проявление одной и той же закономерности и отличающихся по своим характеристикам.

В данной работе рассматриваются и используются для обработки земельно-кадастровых данных следующие статистические методы:

- основные формы, виды и способы статистического наблюдения;

- сводка, группировка данных земельного кадастра;

- абсолютные, относительные и средние величины;

- ряды динамики;

- распределительный метод;

- методы математической обработки данных земельного кадастра.

Таким образом, в земельном кадастре находят широкое применение статистические приемы получения, обработки и анализа необходимых сведений о правовом, природном и хозяйственном состоянии земель.

ГЛАВА 1. Анализ и выравнивание динамических рядов

1. 1. Анализ динамических рядов

Изучение изменения явлений во времени является одной из важных задач статистики. Решается эта задача при помощи составления и анализа рядов динамики. Ряд динамики представляет собой ряд числовых значений определенного статистического показателя в последовательные моменты или периоды времени. Числовые значения того или иного статистического показателя, составляющие динамический ряд, принято называть уровнями ряда (Yi). Одной из основных задач исследования рядов динамики является выявление определенной закономерности в изменении уровней ряда, т. е. основной тенденции изменения уровней, именуемой трендом. Основное требование динамического ряда – сопоставимость уровней.

Виды динамических рядов:

- в зависимости от вида показателей:

1) абсолютные;

2) относительные;

3) средние величины.

- в зависимости от отношений уровня динамического ряда к определенным моментам:

1) моментные – ряды, уровни которых характеризуют величину явления по состоянию на определенные моменты времени;

2) интервальные – ряды, уровни которых характеризуют величину изучаемого показателя, полученную в итоге за определенный период времени.

При составлении уровней динамического ряда анализируются следующие показатели:

1) абсолютный прирост (Аi):

Аi+1=Yi+1 – Yi ,

где i = 1…n, n – число уровней ряда

2) коэффициент роста (Кi) определяется как отношение последующего к предыдущему уровню ряда:

Кi+1=Yi+1 / Yi

3) темп прироста (Тi) – это отношение абсолютного прироста к уровню предыдущего периода (%):

Тi+1=Аi+1 / Yi *100

4) значение 1% прироста (Пi):

Пi+1=Аi+1 / Тi+1 или Пi+1=Yi / 100

5) средний уровень динамического ряда (ỹ) определяется как среднее арифметическое приведенного ряда:

ỹ =/ n

6) средний абсолютный прирост ряда (Ã):

Ã =/ (n-1) = (Yn – Y1) / (n-1)

7) средний коэффициент роста (Ќ):

Ќ = =

Таблица 1.1

Определение показателей динамической урожайности зерновых

Годы	Урожайность, У	Абсолютный прирост, А (ц)	Коэффициент роста, К	Темп прироста, Т (%)	Значение 1% прироста
1	8,0	-	-	-	-
2	8,5	0,5	1,063	6,3	0,08
3	7,8	-0,7	0,918	-8,2	0,09
4	11,9	4,1	1,526	52,6	0,08
5	10,6	-1,3	0,891	-10,9	0,12
6	13,9	3,3	1,311	31,1	0,11
7	14,4	0,5	1,036	3,6	0,14
8	18,3	3,9	1,271	27,1	0,14
9	19,6	1,3	1,071	7,1	0,18
10	20,8	1,2	1,061	6,1	0,20
11	18,2	-2,6	0,875	-12,5	0,21
12	21,9	3,7	1,203	20,3	0,18
13	22,6	0,7	1,032	3,2	0,22
14	22,0	-0,6	0,973	-2,7	0,23
15	25,9	3,9	1,177	17,7	0,22
Итого	244,4	17,9	х	х	Х

Средний уровень динамического ряда: ỹ = 16,3

Средний абсолютный прирост ряда: Ã = 1,28

Средний коэффициент роста: Ќ = 1,088

Таблица 1.2

Определение показателей динамического объема

производственных затрат

Годы	Производствен-ные затраты, Х1	Абсолютный прирост, А	Коэффициент роста, К	Темп прироста, Т (%)	Значение 1% прироста
1	100	-	-	-	-
2	105	5	1,050	5,0	1,00
3	102	-3	0,971	-2,9	1,05
4	111	9	1,088	8,8	1,02
5	115	4	1,036	3,6	1,11
6	120	5	1,043	4,3	1,15
7	130	10	1,083	8,3	1,20
8	140	10	1,077	7,7	1,30
9	165	25	1,179	17,9	1,40
10	176	11	1,067	6,7	1,65
11	188	12	1,068	6,8	1,76
12	213	25	1,133	13,3	1,88
13	250	37	1,174	17,4	2,13
14	259	9	1,036	3,6	2,50
15	270	11	1,042	4,2	2,59
Итого	2444	170	х	х	Х

Средний уровень динамического ряда: ỹ = 162,9

Средний абсолютный прирост ряда: Ã = 12,14

Средний коэффициент роста: Ќ = 1,074

Таблица 1.3

Определение показателей динамического количества

атмосферных осадков

Годы	Атмосферные осадки, Х2	Абсолютный прирост, А	Коэффициент роста, К	Темп прироста, Т (%)	Значение 1% прироста
1	330	-	-	-	-
2	200	-130	0,606	-39,4	3,30
3	126	-74	0,630	-37,0	2,00
4	300	174	2,381	138,1	1,26
5	210	-90	0,700	-30,0	3,00
6	199	-11	0,948	-5,2	2,10
7	210	11	1,055	5,5	1,99
8	246	36	1,171	17,1	2,10
9	145	-101	0,589	-41,1	2,46
10	192	47	1,324	32,4	1,45
11	156	-36	0,813	-18,8	1,92
12	290	134	1,859	85,9	1,56
13	250	-40	0,862	-13,8	2,90
14	220	-30	0,880	-12,0	2,50
15	370	150	1,682	68,2	2,20
Итого	3444	40	х	х	Х

Средний уровень динамического ряда: ỹ = 229,6

Средний абсолютный прирост ряда: Ã = 2,86

Средний коэффициент роста: Ќ = 1,008

1. 2. Выравнивание динамических рядов

Для исключения влияния случайных компонентов динамические ряды подвергаются выравниванию. Выравнивание (сглаживание) динамического ряда может быть проведено несколькими способами:

1) метод укрупнения интервалов:

где k – количество уровней в укрупненном интервале.

2) метод скользящей средней:

;

3) выравнивание по среднему абсолютному приросту:

Ўi =Уi + Ã (i-1) ,

где Ўi - выровненное значение показателя;

Уi – начальное (базисное) значение уровня динамического ряда;

Ã – средний абсолютный прирост (табл. 1.1-1.3).

4) выравнивание по среднему коэффициенту роста:

Ўi =Уi * Ќi-1 ,

где Ќ – средний коэффициент роста (табл. 1.1-1.3).

5) выравнивание по способу наименьших квадратов. Проводится с учетом предполагаемой тенденции изменения показателя. При линейной тенденции выравнивание идет с учетом уравнения:

Ўi = ao + a1t ,

где ao и a1 - параметры линейного уравнения;

t – порядковый номер года в динамическом ряду.

Используя математические преобразования, получаем следующие выражения для нахождения параметров линейного уравнения:

ao = ΣY / n;

a1 = ΣYt / Σt2.

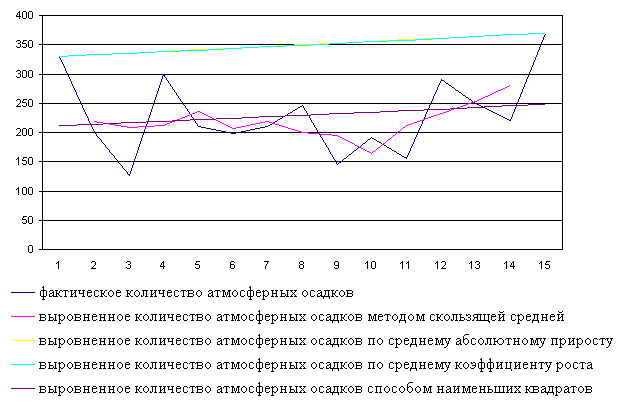
Выравнивание динамических рядов различными методами приводятся в таблицах 2.1 –5.3. Для наглядного представления полученных результатов строятся графики и диаграммы. Как видно из графиков, отражающих выровненные значения показателей по всем методам, наиболее близки к фактическим значениям результаты выравнивания по способу наименьших квадратов.

Таблица 2.1

Выравнивание динамического ряда урожайности зерновых

методом скользящей средней и укрупнений интервалов

Годы	Урожайность зерновых, ц/га	Сумма за трехлетие	Выровненная урожайность	Среднее за трехлетие
1	8,0	Х	Х
2	8,5	24,3	8,1	8,1
3	7,8	28,2	9,4
4	11,9	30,3	10,1
5	10,6	36,4	12,1	12,1
6	13,9	38,9	13,0
7	14,4	46,6	15,5
8	18,3	52,3	17,4	17,4
9	19,6	58,7	19,6
10	20,8	58,6	19,5
11	18,2	60,9	20,3	20,3
12	21,9	62,7	20,9
13	22,6	66,5	22,2
14	22,0	70,5	23,5	23,5
15	25,9	х	Х

Динамика урожайности зерновых (У, ц/га)

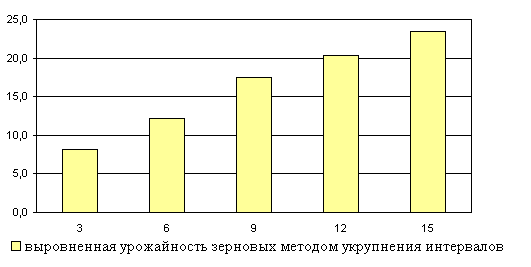
Таблица 2.2

Выравнивание динамического ряда объема производственных затрат

методом скользящей средней и укрупнений интервалов

Годы	Производственные затраты, руб./га	Сумма за трехлетие	Выровненная урожайность	Среднее за трехлетие
1	100	х	Х
2	105	307,0	102,3	102,3
3	102	318,0	106,0
4	111	328,0	109,3
5	115	346,0	115,3	115,3
6	120	365,0	121,7
7	130	390,0	130,0
8	140	435,0	145,0	145,0
9	165	481,0	160,3
10	176	529,0	176,3
11	188	577,0	192,3	192,3
12	213	651,0	217,0
13	250	722,0	240,7
14	259	779,0	259,7	259,7
15	270	х	Х

Динамика производственных затрат (Х1, руб./га)

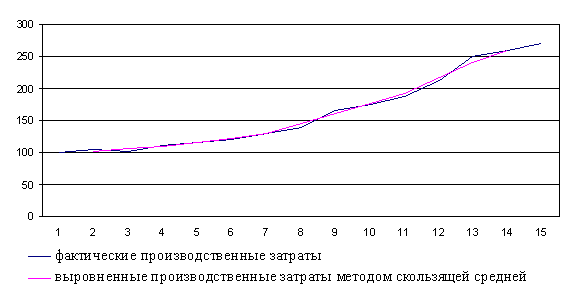
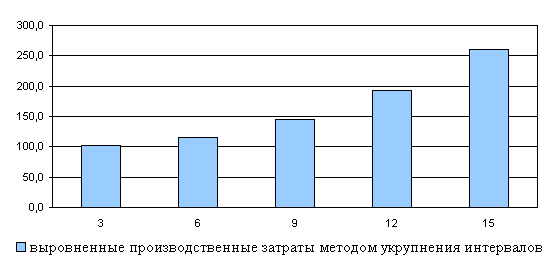
Таблица 2.3

Выравнивание динамического ряда количества атмосферных осадков

методом скользящей средней и укрупнений интервалов

Годы	Атмосферные осадки, мм/год	Сумма за трехлетие	Выровненная урожайность	Среднее за трехлетие
1	330	х	Х
2	200	656,0	218,7	218,7
3	126	626,0	208,7
4	300	636,0	212,0
5	210	709,0	236,3	236,3
6	199	619,0	206,3
7	210	655,0	218,3
8	246	601,0	200,3	200,3
9	145	583,0	194,3
10	192	493,0	164,3
11	156	638,0	212,7	212,7
12	290	696,0	232,0
13	250	760,0	253,3
14	220	840,0	280,0	280,0
15	370	Х	Х

Динамика количества атмосферных осадков (Х2, мм/год)

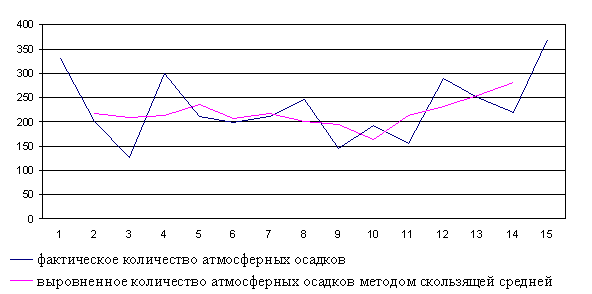
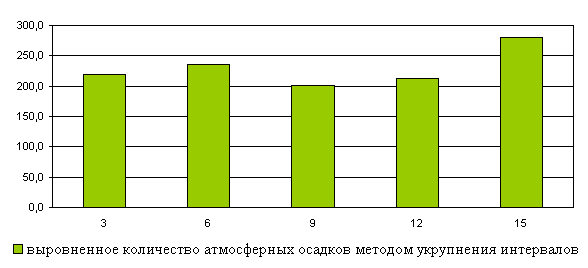
Таблица 3.1

Выравнивание динамического ряда урожайности зерновых

по среднему абсолютному приросту

Ўi=8,0+1,28*(i-1)

Годы	Фактическое значение урожайности зерновых	Выровненное значение урожайности зерновых
1	8,0	8,0
2	8,5	9,3
3	7,8	10,6
4	11,9	11,8
5	10,6	13,1
6	13,9	14,4
7	14,4	15,7
8	18,3	17,0
9	19,6	18,2
10	20,8	19,5
11	18,2	20,8
12	21,9	22,1
13	22,6	23,3
14	22,0	24,6
15	25,9	25,9

Таблица 3.2

Выравнивание динамического ряда производственных затрат

по среднему абсолютному приросту

Х1i=100+12,14*(i-1)

Годы	Фактическое значение производственных затрат	Выровненное значение производственных затрат
1	100,0	100,0
2	105,0	112,1
3	102,0	124,3
4	111,0	136,4
5	115,0	148,6
6	120,0	160,7
7	130,0	172,9
8	140,0	185,0
9	165,0	197,1
10	176,0	209,3
11	188,0	221,4
12	213,0	233,6
13	250,0	245,7
14	259,0	257,9
15	270,0	270,0

Таблица 3.3

Выравнивание динамического ряда количества атмосферных осадков

по среднему абсолютному приросту

Х2i=330+2,86*(I-1)

Годы	Фактическое значение атмосферных осадков	Выровненное значение атмосферных осадков
1	330,0	330,0
2	200,0	332,9
3	126,0	335,7
4	300,0	338,6
5	210,0	341,4
6	199,0	344,3
7	210,0	347,1
8	246,0	350,0
9	145,0	352,9
10	192,0	355,7
11	156,0	358,6
12	290,0	361,4
13	250,0	364,3
14	220,0	367,1
15	370,0	370,0

Таблица 4.1

Выравнивание динамического ряда урожайности зерновых

по среднему коэффициенту роста

Уi=8,0*1,088i-1

Годы	Фактическое значение урожайности зерновых	Выровненное значение урожайности зерновых
1	8,0	8,0
2	8,5	8,7
3	7,8	9,5
4	11,9	10,3
5	10,6	11,2
6	13,9	12,2
7	14,4	13,2
8	18,3	14,4
9	19,6	15,7
10	20,8	17,0
11	18,2	18,5
12	21,9	20,1
13	22,6	21,9
14	22,0	23,8
15	25,9	25,9

Таблица 4.2

Выравнивание динамического ряда производственных затрат

по среднему коэффициенту роста

Х1i=100,0*1,074i-1

Годы	Фактическое значение производственных затрат	Выровненное значение производственных затрат
1	100,0	100,0
2	105,0	107,4
3	102,0	115,2
4	111,0	123,7
5	115,0	132,8
6	120,0	142,6
7	130,0	153,1
8	140,0	164,3
9	165,0	176,4
10	176,0	189,4
11	188,0	203,3
12	213,0	218,2
13	250,0	234,3
14	259,0	251,5
15	270,0	270,0

Таблица 4.3

Выравнивание динамического ряда количества атмосферных осадков

по среднему коэффициенту роста

Х2i=330,0*1,008i-1

Годы	Фактическое значение атмосферных осадков	Выровненное значение атмосферных осадков
1	330,0	330,0
2	200,0	332,7
3	126,0	335,4
4	300,0	338,2
5	210,0	341,0
6	199,0	343,8
7	210,0	346,6
8	246,0	349,4
9	145,0	352,3
10	192,0	355,2
11	156,0	358,1
12	290,0	361,0
13	250,0	364,0
14	220,0	367,0
15	370,0	370,0

Таблица 5.1

Выравнивание урожайности зерновых

способом наименьших квадратов

Годы	Фактическая урожайность зерновых, ц/га	Ранг года t	Уi*ti	t2	Выровненная урожайность зерновых, ц/га
1	8,0	-7	-56,0	49	7,2
2	8,5	-6	-51,0	36	8,5
3	7,8	-5	-39,0	25	9,8
4	11,9	-4	-47,6	16	11,1
5	10,6	-3	-31,8	9	12,4
6	13,9	-2	-27,8	4	13,7
7	14,4	-1	-14,4	1	15,0
8	18,3	0	0,0	0	16,3
9	19,6	1	19,6	1	17,6
10	20,8	2	41,6	4	18,9
11	18,2	3	54,6	9	20,2
12	21,9	4	87,6	16	21,5
13	22,6	5	113,0	25	22,8
14	22,0	6	132,0	36	24,1
15	25,9	7	181,3	49	25,3
Итого	244,4	0,0	362,1	280,0	х

Динамика роста урожайности зерновых

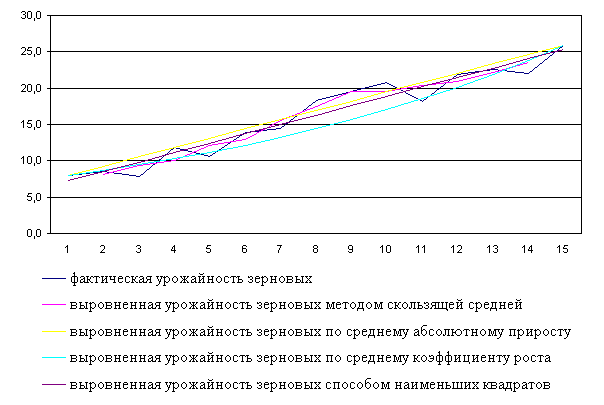
Таблица 5.2

Выравнивание производственных затрат

способом наименьших квадратов

Годы	Фактические производственные затраты, руб./га	Ранг года t	Уi*ti	t2	Выровненная производственные затраты, руб/га
1	100	-7	-700,0	49	72,2
2	105	-6	-630,0	36	85,2
3	102	-5	-510,0	25	98,1
4	111	-4	-444,0	16	111,1
5	115	-3	-345,0	9	124,1
6	120	-2	-240,0	4	137,0
7	130	-1	-130,0	1	150,0
8	140	0	0,0	0	162,9
9	165	1	165,0	1	175,9
10	176	2	352,0	4	188,8
11	188	3	564,0	9	201,8
12	213	4	852,0	16	214,8
13	250	5	1250,0	25	227,7
14	259	6	1554,0	36	240,7
15	270	7	1890,0	49	253,6
Итого	2444,0	0,0	3628,0	280,0	х

Динамика роста производственных затрат

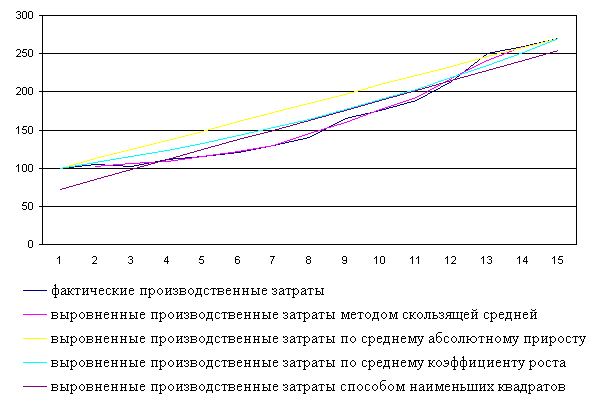
Таблица 5.3

Выравнивание количества атмосферных осадков

способом наименьших квадратов

Годы	Фактические атмосферные осадки, мм/год	Ранг года t	Уi*ti	t2	Выровненные атмосферные осадки, мм/год
1	330	-7	-2310,0	49	211,1
2	200	-6	-1200,0	36	213,8
3	126	-5	-630,0	25	216,4
4	300	-4	-1200,0	16	219,0
5	210	-3	-630,0	9	221,7
6	199	-2	-398,0	4	224,3
7	210	-1	-210,0	1	227,0
8	246	0	0,0	0	229,6
9	145	1	145,0	1	232,2
10	192	2	384,0	4	234,9
11	156	3	468,0	9	237,5
12	290	4	1160,0	16	240,2
13	250	5	1250,0	25	242,8
14	220	6	1320,0	36	245,4
15	370	7	2590,0	49	248,1
Итого	3444,0	0,0	739,0	280,0	х

Динамика роста количества атмосферных осадков

ГЛАВА 2. Вариационные ряды

2. 1. Построение и анализ вариационных рядов

Первым шагом систематизации материалов статистического наблюдения является подсчет числа единиц, обладающих тем или иным признаком. Расположив единицы в порядке возрастания или убывания их количественного признака и подсчитав число единиц с конкретным значением признака, получаем вариационный ряд. Другими словами, вариационный ряд характеризует распределение единиц определенной статистической совокупности по какому-либо количественному признаку. Вариационный ряд – это ряд чисел, показывающий, каким образом числовые значения признака связаны с их повторяемостью. Количество повторяемости – частота или веса вариантов (F).

При кадастровой оценке земель используется сплошной метод, т. е. исходные данные берутся по всем хозяйствам земельно-оценочного района и не могут быть нормально распределены из-за различного уровня интенсивности сельскохозяйственного производства колхозов и совхозов. Поэтому нормально распределены должны быть результативные показатели, отнесенные к единице производственных факторов.

Анализ вариационного ряда начинают с определения показателей вариации:

1) размах вариации (R) характеризует колебания максимального и минимального значения переменной:

R = Xmax – Xmin ;

2) среднее квадратическое отклонение (σ) наиболее объективно характеризует колеблемость:

σ = ,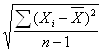

где – среднеарифметическое значение переменных ряда;

3) нормированное отклонение вариационного ряда проверяет нормальность распределения переменных в нем:

t = ;

Нормальное распределение – распределение, описывающееся плотностью. Кривая нормального распределения – кривая, изображающая плотность распределения. Она выражается формулой Гаусса-Лапласа:

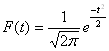Асимметрия – мера косости распределения. Этот показатель характеризует горизонтальное отклонение кривой F(t) от кривой нормального распределения (влево или вправо):

Эксцесс – мера крутости распределения. Характеризует вертикальное отклонение кривой нормального распределения:

2. 2 Статистическая группировка земельно-кадастровых показателей

и построение статистических таблиц

При обработке статистических материалов возникает необходимость выделения однородных групп, типов, а затем уже описание этих групп определенными количественными характеристиками. Расчленение совокупности на группы, однородные по какому-либо признаку, называется группировкой. Для ее проведения необходимо определить те характеристики (группировочные признаки), по которым она будет проводиться, и их значений, отделяющих одну группу от другой (интервалы группировки).

В данной работе группировка будет проводиться по таким важным экономическим показателям, как урожайность, стоимость валовой продукции и чистого дохода на 1 га сельскохозяйственных угодий. Для этого в таблицах 7.1 – 7.5 производится расчет валовой продукции, чистого дохода и производственных затрат по всем культурам в 20 хозяйствах с использованием следующих формул:

- валовая продукция: ,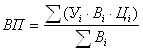

где Вi – удельный вес культуры в данном хозяйстве;

Уi – урожайность культуры;

Цi – кадастровая цена за 1 ц продукции.

- производственные затраты: ,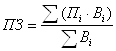

где Пi – производственные затраты по i-ой культуре.

- чистый доход: .

По способу составления группировка может быть первичной и вторичной. Величина интервала превичной группировки (h) определяется по формуле:

h = (Xmax – Xmin) / K,

где Xmax и Xmin – максимальное и минимальное значения признака;

К – количество групп, на которые подразделяются хозяйства. Определяется по формуле Стерджеса:

K = 1+1,32*lg n.

При вторичной группировке количество хозяйств в группе одинаково или несильно отличается, введены открытые интервалы. При комбинированной группировке производится выделение подгрупп в каждой группе по какому-либо другому показателю (возможна группировка и более чем по двум показателям). В таблицах 9.1-9.8 выделены группы хозяйств по урожайности культур, которые подразделяются на подгруппы по баллу бонитета по свойствам почв. Анализируя полученные результаты, видим, что при общей зависимости урожайности от количества применяемых удобрений по группам, наблюдается более высокая отдача на земле с более высоким баллом бонитета почв.

Для выявления причин, определяющих величину чистого дохода, строится аналитическая таблица 10, в которую включаются 5 факторов: валовая продукция, производственные затраты, основные производственные фонды, затраты живого труда и затраты удобрений.

ГЛАВА 3. Математическая обработка исходной информации

3. 1. Определение тесноты связи между результатирующим фактором и факторами, влияющими на него, а также

тесноты связи между самими влияющими факторами

Таблица 11

Исходные данные

№№ п/п	Урожайность естеств. сенокосов, ц/га	Влияющие факторы
№№ п/п	Урожайность естеств. сенокосов, ц/га	Производств. затраты, руб./га	Основные произв. фонды, руб./га	Затраты мин. удобрений, ц/га	Энергетические мощности, л. с.	Удельный вес залес. и закуст. сенокосов, %	Удельный вес заболоченных сенокосов, %	Удельный вес улучшенных сенокосов, %	Балл оценки по совокупным свойствам почв
1	12,2	54,0	600	0,81	2,00	20,0	1,6	11,6	51
2	11,4	70,8	400	0,50	1,40	38,0	9,6	12,3	60
3	11,1	160,0	602	2,25	3,10	22,0	3,5	6,0	55
4	21,1	110,0	680	1,50	1,75	9,6	3,0	42,0	86
5	10,8	71,0	450	0,76	1,68	40,0	26,5	8,0	55
6	11,1	75,0	420	0,65	1,10	32,0	13,0	26,1	61
7	13,9	60,0	380	2,14	1,80	25,0	5,2	7,9	72
8	9,0	64,4	450	0,80	1,90	30,0	5,0	22,3	50
9	17,0	120,0	715	1,31	2,55	7,0	0,5	40,0	92
10	11,7	64,0	350	0,69	1,56	31,0	8,0	35,0	45
11	10,6	70,0	410	1,12	1,80	26,4	14,2	15,2	61
12	12,7	62,5	500	1,58	1,78	21,5	24,0	20,0	84
13	14,0	55,0	620	1,05	1,40	33,6	6,1	12,4	78
14	12,5	60,0	550	0,90	1,70	19,0	60,0	15,0	72
15	12,1	85,0	550	0,70	1,60	40,0	9,0	2,0	76
16	12,0	70,0	560	0,75	1,86	20,0	1,0	13,0	60
17	15,8	108,0	420	0,74	1,23	18,5	4,7	25,0	86
18	12,6	85,0	680	0,90	2,31	32,6	8,4	17,4	81
19	27,3	147,0	621	0,70	3,75	1,58	0,5	9,9	92
20	18,9	78,0	480	1,12	2,68	40,0	12,8	8,6	90
21	14,3	55,6	568	0,88	1,74	18,8	2,5	6,0	96
22	8,8	45,4	340	0,68	1,01	26,0	48,4	12,5	54
23	13,5	68,0	508	1,32	2,14	42,4	11,0	10,6	74

Теснота и направление парной линейной корреляционной зависимости переменных Х и Y определяется коэффициентом корреляции. Он принимает значения от –1 до +1. При связь тесная, фактор, оказывающий влияние на результирующий показатель достоверен. При связь практически отсутствует и рассматриваемый фактор следует исключить.

Связь между результирующим и влияющими факторами отражается уравнением множественной линейной регрессии:

Y=Ao + A1X1 + A2X2 +…+ AnXn ,

где Ao – свободный член уравнения, экономической интерпретации не имеет;

A1,A2,…,An – коэффициенты уравнения, показывающие на сколько изменится результирующий фактор при изменении влияющего на единицу;

X1, X2,…,Xn – значения влияющих факторов.

В результате решения задачи с помощью “Regma” были получены следующие коэффициенты уравнения множественной линейной регрессии:

A[ 0]= 3.3854

A[ 1]= 0.0101

A[ 2]= -0.0076

A[ 3]= -1.7198

A[ 4]= 2.9394

A[ 5]= -0.0764

A[ 6]= -0.0252

A[ 7]= 0.0501

A[ 8]= 0.1559

Приведенное значение среднего квадратического отклонения фактических значений результирующего показателя от его вычисленных значений = 0.1376.

Коэффициент множественной корреляции = 0.89.

Коэффициент детерминации = 0.79.

Пакет программных средств “Regma” позволяет отбраковать факторы, не влияющие или мало влияющие на результирующий. Первоначально при расчете используются все факторы, которые могут влиять. В полученных результатах отражается теснота связи между результирующим фактором и факторами, влияющими на него (I матрица результатов), а также связь между самими влияющими факторами (II матрица результатов).

Таблица 12

Характеристики рядов исходной матрицы (I)

Ряд	среднее	Среднее квадратич. отклонение	энтропия	эластичность	Коэф. вариации	Бета-коэф.
1	13,67	4,07	1,41	3,39	0,30	3,39
2	79,94	29,09	2,39	0,06	0,36	0,07
3	515,39	107,77	3,05	-0,29	0,21	-0,20
4	1,04	0,45	0,31	-0,13	0,44	-0,19
5	1,91	0,62	0,47	0,41	0,33	0,45
6	25,87	10,78	1,90	0,14	0,42	-0,20
7	12,11	14,68	2,05	-0,02	1,21	-0,09
8	16,47	10,56	1,89	0,06	0,64	0,13
9	70,91	15,37	2,07	0,81	0,22	0,59

Таблица 13

Характеристики рядов исходной матрицы (II)

Ряд	Макс. значение	Мин. значение	энтропия
1	27,30	8,80	4,21
2	160,00	45,40	6,84
3	715,00	340,00	8,55
4	2,25	0,50	0,81
5	3,75	1,01	1,45
6	42,40	1,58	5,35
7	60,00	0,50	5,89
8	42,00	2,00	5,32
9	96,00	45,00	5,67

Таблица 14

Таблица парных коэффициентов корреляции

пара	Коэф. корреляции	Оценка существ.	энтропия
1-2	0,5627	3,1928	19,9089
1-3	0,4762	2,5400	16,6867
1-4	0,0935	0,4407	7,9087
1-5	0,6006	3,5230	8,4706
1-6	-0,5608	-3,1774	12,2834
1-7	-0,3411	-1,7018	11,3714
1-8	0,1771	0,8439	11,8814
1-9	0,7180	4,8378	13,4880
2-3	0,4725	2,5148	19,2380
2-4	0,3262	1,6187	10,3819
2-5	0,6947	4,5305	10,8659
2-6	-0,4871	-2,6162	14,9084
2-7	-0,3975	-2,0319	13,8846
2-8	0,1661	0,7900	14,4323
2-9	0,3056	1,5056	16,4879
3-4	0,2068	0,9917	13,1201
3-5	0,5333	2,9570	13,7885
3-6	-0,4547	-2,3948	17,6253
3-7	-0,3327	-1,6546	16,6127
3-8	0,1326	0,6277	17,1282
3-9	0,5129	2,8400	19,0220
4-5	0,3471	1,7361	4,9801
4-6	-0,1836	-0,8759	8,8106
4-7	-0,1560	-0,7407	7,7223
4-8	-0,0148	-0,0694	8,1837
4-9	0,1656	0,7875	10,2701
5-6	-0,3767	-1,9075	9,6031
5-7	-0,3500	-1,7527	8,5241
5-8	-0,1596	-0,7585	-,0435
5-9	0,3196	1,5821	11,0907
6-7	0,1558	0,7399	12,3632
6-8	-0,3928	-2,0037	12,7037
6-9	-0,3666	-1,8484	14,8268
7-8	-0,1351	-0,6395	11,7162
7-9	-0,1905	-0,9100	13,8091
8-9	0,0661	0,3107	14,2763

В I матрице отбраковываются факторы, не влияющие или мало влияющие на результирующий (), а во II матрице исключается мультикоррелярность, означающая, что факторы являются результатом друг друга (). Для исключения одного из двух влияющих факторов необходимо определить, какой из них имеет меньшую тесноту связи с результирующим (рассматривается матрица I).

В I матрице исключаются 4 и 8 факторы (т. к. 1 фактором является урожайность, следовательно, исключаются Х3 и Х7). Во второй исключать ничего не пришлось. После исключения малозначащих и мультикорреляционных факторов снова производится обработка исходной числовой матрицы.

A[ 0]= 4.4290

A[ 1]= 0.0114

A[ 2]= -0.0069

A[ 4]= 2.1302

A[5]= -0.0967

A[ 6]= -0.0297

A[ 8]= 0.1508

Приведенное значение среднего квадратического отклонения фактических значений результирующего показателя от его вычисленных значений = 0.1508

Коэффициент множественной корреляции = 0.86

Коэффициент детерминации = 0.74

Таблица 15

Характеристики рядов исходной матрицы (I)

Ряд	среднее	Среднее квадратич. отклонение	энтропия	эластичность	Коэф. вариации	Бета-коэф.
1	13,67	4,07	1,41	4,43	0,30	4,43
2	79,94	29,09	2,39	0,07	0,36	0,08
3	515,39	107,77	3,05	-0,26	0,21	-0,18
5	1,91	0,62	0,47	0,30	0,33	0,33
6	25,87	10,78	1,90	-0,18	0,42	-0,26
7	12,11	14,68	2,05	-0,03	1,21	-0,11
9	70,91	15,37	2,07	0,78	0,22	0,57

Таблица 16

Таблица парных коэффициентов корреляции

пара	Коэф. корреляции	Оценка существ.	энтропия
1-2	0,5627	3,1928	19,9089
1-3	0,4762	2,5400	16,6867
1-5	0,6006	3,5230	8,4706
1-6	-0,5608	-3,1774	12,2834
1-7	-0,3411	-1,7018	11,3714
1-9	0,7180	4,8378	13,4880
2-3	0,4725	2,5148	19,2380
2-5	0,6947	4,5305	10,8659
2-6	-0,4871	-2,6162	14,9084
2-7	-0,3975	-2,0319	13,8846
2-9	0,3056	1,5056	16,4879
3-5	0,5333	2,9570	13,7885
3-6	-0,4547	-2,3948	17,6253
3-7	-0,3327	-1,6546	16,6127
3-9	0,5129	2,8400	19,0220
5-6	-0,3767	-1,9075	9,6031
5-7	-0,3500	-1,7527	8,5241
5-9	0,3196	1,5821	11,0907
6-7	0,1558	0,7399	12,3632
6-9	-0,3666	-1,8484	14,8268
7-9	-0,1905	-0,9100	13,8091

3. 2. Графическое отображение связи между результирующим фактором и фактором, в наибольшей степени на него влияющим

По результатам повторной обработки исходной числовой матрицы определяется фактор, имеющий наибольшее влияние на результирующий (величина коэффициента корреляции близка к 1). В данной матрице это 9 фактор. Пакет программных средств “Coreg” позволяет наглядно отразить связь между результирующим фактором и фактором в наибольшей степени на него влияющим.

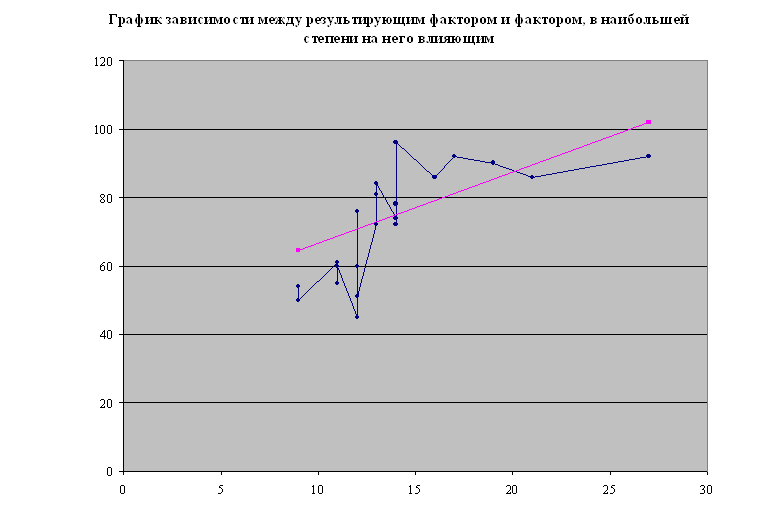
Таблица 6.1.

Расчет исходных данных для проверки нормальности распределения вариационного ряда

урожайности ячменя по затратам удобрений (Х)

№№ по порядку	Урожайность ячменя с 1 га, У	Затраты удобрений на 1 га посевов ц. д. в., Х	Урожайность в расчете на 1 ц удобрений, ц с 1 га, Уt	(У-Ў)2	(Уt-Ўt)	(Уt-Ўt)2	(Уt-Ўt)3	(Уt-Ўt)4		Ордината нормальной кривой F(t)
1	25,2	3,34	7,54	58,68	-0,35	0,12	-0,04	0,01	-0,35	0,3614
2	23,0	2,89	7,96	29,81	0,07	0,00	0,00	0,00	0,07	0,3975
3	21,5	2,79	7,71	15,68	-0,19	0,03	-0,01	0,00	-0,19	0,3878
4	20,4	2,49	8,19	8,18	0,30	0,09	0,03	0,01	0,30	0,3702
5	20,9	2,39	8,74	11,29	0,85	0,73	0,62	0,53	0,85	0,2190
6	19,4	2,35	8,26	3,46	0,36	0,13	0,05	0,02	0,36	0,3577
7	19,4	2,35	8,26	3,46	0,36	0,13	0,05	0,02	0,36	0,3577
8	18,6	2,18	8,53	1,12	0,64	0,41	0,26	0,17	0,64	0,2845
9	18,2	2,18	8,35	0,44	0,46	0,21	0,10	0,04	0,46	0,3358
10	17,4	2,04	8,53	0,02	0,64	0,41	0,26	0,17	0,64	0,2853
11	17,4	2,04	8,53	0,02	0,64	0,41	0,26	0,17	0,64	0,2853
12	16,8	2,00	8,40	0,55	0,51	0,26	0,13	0,07	0,51	0,3224
13	16,8	2,00	8,40	0,55	0,51	0,26	0,13	0,07	0,51	0,3224
14	16,0	1,93	8,29	2,37	0,40	0,16	0,06	0,03	0,40	0,3500
15	15,1	1,93	7,82	5,95	-0,07	0,00	0,00	0,00	-0,07	0,3974
16	15,1	1,93	7,82	5,95	-0,07	0,00	0,00	0,00	-0,07	0,3974
17	14,1	1,90	7,42	11,83	-0,47	0,22	-0,10	0,05	-0,47	0,3325
18	13,0	1,90	6,84	20,61	-1,05	1,10	-1,16	1,21	-1,05	0,1611
19	12,2	1,84	6,63	28,52	-1,26	1,59	-2,00	2,53	-1,26	0,1077
20	10,3	1,84	5,60	52,42	-2,29	5,26	-12,06	27,67	-2,29	0,0052
сумма	350,8	44,31	157,83	260,91	0,00	11,53	-13,43	32,75	х	х

σост. факторов = 0,78; σ2 ост. факторов = 0,61; σ2 общ =13,73; σ2 уд= 13,12.

Аs = -1,419; Ех = 1,443.

Распределение урожайности ячменя по затратам удобрений

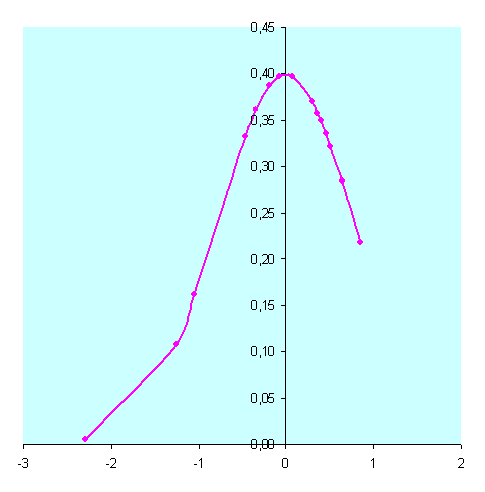
Таблица 6.2.

Расчет исходных данных для проверки нормальности распределения вариационного ряда

урожайности овса по затратам удобрений (Х)

№№ по порядку	Урожайность овса с 1 га, У	Затраты удобрений на 1 га посевов ц. д. в., Х	Урожайность в расчете на 1 ц удобрений, ц с 1 га, Уt	(У-Ў)2	(Уt-Ўt)	(Уt-Ўt)2	(Уt-Ўt)3	(Уt-Ўt)4		Ордината нормальной кривой F(t)
1	24,2	3,34	7,25	21,67	-1,61	2,60	-4,19	6,76	-1,61	0,1214
2	24,2	2,89	8,37	21,67	-0,48	0,23	-0,11	0,06	-0,48	0,3583
3	23,3	2,79	8,35	14,10	-0,51	0,26	-0,13	0,07	-0,51	0,3547
4	22,2	2,49	8,92	7,05	0,06	0,00	0,00	0,00	0,06	0,3983
5	22,2	2,39	9,29	7,05	0,43	0,19	0,08	0,03	0,43	0,3665
6	21,7	2,35	9,23	4,64	0,38	0,14	0,05	0,02	0,38	0,3740
7	21,2	2,35	9,02	2,74	0,16	0,03	0,00	0,00	0,16	0,3941
8	20,8	2,18	9,54	1,58	0,68	0,47	0,32	0,22	0,68	0,3222
9	20,8	2,18	9,54	1,58	0,68	0,47	0,32	0,22	0,68	0,3222
10	20,1	2,04	9,85	0,31	0,99	0,99	0,98	0,98	0,99	0,2537
11	20,1	2,04	9,85	0,31	0,99	0,99	0,98	0,98	0,99	0,2537
12	19,4	2,00	9,70	0,02	0,84	0,71	0,60	0,50	0,84	0,2885
13	19,4	2,00	9,70	0,02	0,84	0,71	0,60	0,50	0,84	0,2885
14	18,7	1,93	9,69	0,71	0,83	0,69	0,57	0,48	0,83	0,2909
15	18,2	1,93	9,43	1,81	0,57	0,33	0,19	0,11	0,57	0,3435
16	18,6	1,93	9,64	0,89	0,78	0,61	0,47	0,37	0,78	0,3022
17	16,2	1,90	8,53	11,19	-0,33	0,11	-0,04	0,01	-0,33	0,3793
18	15,2	1,90	8,00	18,88	-0,86	0,74	-0,63	0,54	-0,86	0,2848
19	13,2	1,84	7,17	40,26	-1,68	2,84	-4,78	8,05	-1,68	0,1090
20	11,2	1,84	6,09	69,64	-2,77	7,68	-21,28	58,97	-2,77	0,0119
сумма	390,9	44,31	177,16	226,11	0,00	20,77	-25,99	78,86	х	х

σост. факторов = 1,05; σ2 ост. факторов = 1,09; σ2 общ = 11,90; σ2 уд= 10,81.

Аs = -1,137; Ех = 0,301.

Распределение урожайности овса по затратам удобрений

Таблица 6.3.

Расчет исходных данных для проверки нормальности распределения вариационного ряда

урожайности многолетних трав по затратам удобрений (Х)

№№ по порядку	Урожайность многолетних трав с 1 га, У	Затраты удобрений на 1 га посевов ц. д. в., Х	Урожайность в расчете на 1 ц удобрений, ц с 1 га, Уt	(У-Ў)2	(Уt-Ўt)	(Уt-Ўt)2	(Уt-Ўt)3	(Уt-Ўt)4		Ордината нормальной кривой F(t)
1	29,6	3,34	8,86	136,89	1,03	1,05	1,08	1,11	1,03	0,3552
2	27,6	2,89	9,55	94,09	1,71	2,94	5,03	8,62	1,71	0,2884
3	27,1	2,79	9,71	84,64	1,88	3,52	6,61	12,40	1,88	0,2704
4	25,9	2,49	10,40	64,00	2,57	6,58	16,88	43,29	2,57	0,1929
5	25,6	2,39	10,71	59,29	2,87	8,26	23,76	68,29	2,87	0,1601
6	24,1	2,35	10,26	38,44	2,42	5,85	14,15	34,23	2,42	0,2090
7	22,6	2,35	9,62	22,09	1,78	3,17	5,64	10,05	1,78	0,2811
8	20,6	2,18	9,45	7,29	1,61	2,60	4,20	6,77	1,61	0,2993
9	19,6	2,18	8,99	2,89	1,15	1,33	1,54	1,77	1,15	0,3443
10	18,6	2,04	9,12	0,49	1,28	1,64	2,10	2,69	1,28	0,3328
11	17,6	2,04	8,63	0,09	0,79	0,63	0,49	0,39	0,79	0,3723
12	15,6	2,00	7,80	5,29	-0,04	0,00	0,00	0,00	-0,04	0,3989
13	13,6	2,00	6,80	18,49	-1,04	1,07	-1,11	1,15	-1,04	0,3543
14	11,6	1,93	6,01	39,69	-1,83	3,34	-6,09	11,12	-1,83	0,2760
15	10,6	1,93	5,49	53,29	-2,34	5,50	-12,88	30,21	-2,34	0,2174
16	10,4	1,93	5,39	56,25	-2,45	5,99	-14,67	35,91	-2,45	0,2058
17	9,6	1,90	5,05	68,89	-2,78	7,75	-21,58	60,07	-2,78	0,1695
18	9,5	1,90	5,00	70,56	-2,84	8,05	-22,82	64,74	-2,84	0,1640
19	9,2	1,84	5,00	75,69	-2,84	8,05	-22,82	64,74	-2,84	0,1640
20	9,0	1,84	4,89	79,21	-2,95	8,67	-25,55	75,25	-2,95	0,1530
сумма	358,0	44,31	156,73	977,56	0,00	85,99	-46,05	532,81	х	х

σост. факторов = 2,13; σ2 ост. факторов = 4,53; σ2 общ = 51,45; σ2 уд= 46,92.

Аs = -0,239; Ех = -1,699.

Распределение урожайности многолетних трав по затратам удобрений

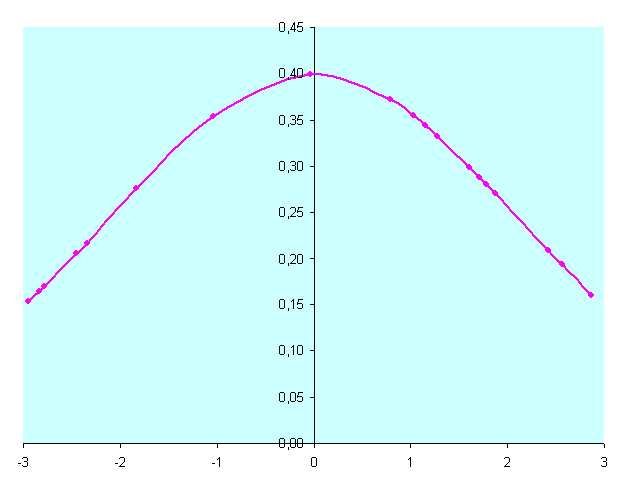
Таблица 7.1

Основные экономические показатели (на 1 га пашни) в растениеводстве

№№ хозяйств	Основные производственные фонды, руб.	Затраты живого труда, чел/час	Затраты удобрений, ц. д. в.
1	1986	154	3,34
2	1921	149	2,89
3	1868	124	2,79
4	1826	109	2,49
5	1725	109	2,39
6	1618	104	2,35
7	1585	104	2,35
8	1585	99	2,18
9	1577	94	2,18
10	1514	94	2,04
11	1472	88	2,04
12	1439	79	2,00
13	1439	76	2,00
14	1402	74	1,93
15	1402	71	1,93
16	1367	69	1,93
17	1367	65	1,90
18	1330	59	1,90
19	1328	49	1,84
20	1328	49	1,84

Таблица 7.2

Урожайность сельскохозяйственных культур (ц с 1 га) в среднем за год

№№ хозяйств	Озимая пшеница	Озимая рожь	Яровая пшеница	Ячмень	Овес	Многолет. травы	Картофель	Кукуруза	Балл бонитета
1	33,5	35,8	26,0	25,2	24,2	29,6	300,0	210,0	87
2	31,5	34,3	26,0	23,0	24,2	27,6	292,0	195,0	98
3	28,0	34,3	23,0	21,5	23,3	27,1	285,0	194,0	58
4	25,0	33,0	23,0	20,4	22,2	25,9	274,0	190,0	43
5	22,5	32,3	22,0	20,9	22,2	25,6	266,0	190,0	84
6	22,5	30,8	21,0	19,4	21,7	24,1	242,0	182,0	90
7	22,8	30,3	21,0	19,4	21,2	22,6	231,0	171,0	57
8	21,9	29,4	20,0	18,6	20,8	20,6	222,0	170,0	43
9	20,7	27,2	20,0	18,2	20,8	19,6	201,0	164,0	83
10	19,7	26,4	19,0	17,4	20,1	18,6	190,0	154,0	84
11	19,7	25,5	19,0	17,4	20,1	17,6	187,0	153,0	61
12	18,9	23,2	18,0	16,8	19,4	15,6	172,0	142,0	45
13	18,6	23,4	18,0	16,8	19,4	13,6	162,0	133,0	94
14	18,0	22,4	17,0	16,0	18,7	11,6	151,0	122,0	85
15	18,0	21,2	16,5	15,1	18,2	10,6	143,0	116,0	50
16	17,1	20,3	16,0	15,1	18,6	10,4	138,0	111,0	65
17	17,0	18,2	14,5	14,1	16,2	9,6	130,0	102,0	81
18	16,1	17,5	14,0	13,0	15,2	9,5	130,0	100,0	78
19	15,7	16,5	13,5	12,2	13,2	9,2	127,0	87,0	37
20	15,0	10,0	12,4	10,3	11,2	9,0	125,0	80,0	57

Таблица 7.3

Производственные затраты (руб. на 1 га)

№№ хозяйств	Озимая пшеница	Озимая рожь	Яровая пшеница	Ячмень	Овес	Многолет. травы	Картофель	Кукуруза
1	216,0	230,0	206,0	200,0	200,0	96,0	1510,0	200,0
2	211,0	225,0	203,0	198,0	196,5	91,5	1500,0	196,0
3	191,0	221,0	199,0	193,5	193,0	88,0	1490,0	192,0
4	211,0	217,0	196,0	190,0	189,0	85,0	1474,0	183,0
5	186,0	212,0	193,0	187,0	186,2	80,0	1460,0	176,0
6	223,5	107,0	190,0	183,5	182,8	75,5	1449,0	170,0
7	173,5	164,0	186,5	180,5	179,3	72,0	1438,0	164,0
8	185,5	180,0	182,9	177,0	175,0	67,2	1425,0	158,0
9	180,5	197,0	180,0	174,0	172,0	62,4	1410,0	151,0
10	179,0	193,0	178,0	170,4	169,0	60,5	1395,0	145,0
11	165,3	190,0	176,0	167,0	165,5	60,0	1390,0	14,0
12	172,0	190,0	171,5	163,5	162,1	56,2	1374,0	135,0
13	131,0	190,0	167,0	160,0	160,0	52,0	1367,0	129,0
14	172,0	189,7	164,4	156,6	158,3	48,0	1351,0	124,0
15	121,0	175,8	162,0	153,0	155,0	44,5	1343,0	118,0
16	154,0	172,0	159,5	14,4	151,6	40,3	1332,0	109,0
17	154,0	167,9	157,1	145,8	148,2	36,6	1318,0	108,0
18	135,0	164,2	154,7	142,2	144,9	32,6	1305,0	108,0
19	150,0	160,0	152,4	138,6	141,4	23,9	1293,0	96,0
20	145,0	156,0	150,0	135,0	138,0	25,0	1280,0	90,0

Таблица 7.4

Структура посевных площадей (% от общей площади)

№№ хозяйств	Озимая пшеница	Озимая рожь	Яровая пшеница	Ячмень	Овес	Многолет. травы	Картофель	Кукуруза
1	11	8	13	15	12	25	12	4
2	10	12	12	16	11	25	11	3
3	12	11	9	14	9	28	13	4
4	11	12	13	15	14	23	10	2
5	12	13	12	13	13	23	9	5
6	11	13	16	10	13	23	10	4
7	11	5	10	16	12	27	14	5
8	10	8	13	12	15	26	10	6
9	11	8	15	9	13	25	14	4
10	10	9	13	14	13	25	12	4
11	9	9	14	16	12	25	10	5
12	8	11	10	17	11	26	12	5
13	10	11	15	16	13	25	6	4
14	7	10	15	13	12	25	15	3
15	7	9	13	17	12	27	10	5
16	9	7	15	15	13	25	12	4
17	9	9	17	13	12	24	12	5
18	12	9	16	14	13	23	10	3
19	9	8	15	17	14	23	11	3
20	11	8	16	15	15	22	9	4

Таблица 7.5

Расчет стоимости продукции, размеры производственных затрат

и чистого дохода в хозяйствах

№№ хозяйств	Валовая продукция	Производственные затраты	Чистый доход
1	1500,1	336,1	1163,9
2	1384,1	319,5	1064,6
3	1446,9	335,6	1111,3
4	1222,9	300,3	922,6
5	1141,7	280,2	861,6
6	1118,4	280,1	838,3
7	1258,9	325,3	933,6
8	1028,3	273,7	754,6
9	1129,3	319,7	809,7
10	995,6	292,6	703,0
11	903,2	257,9	645,3
12	910,2	283,7	626,5
13	669,1	205,6	463,5
14	917,9	313,4	604,5
15	714,7	242,2	472,5
16	761,4	246,0	515,4
17	716,1	264,8	451,4
18	641,6	235,7	405,8
19	640,5	243,1	397,4
20	544,2	217,7	326,6
Итого по хозяйствам	19645,2	5573,0	14072,2
В среднем по хозяйствам	982,3	278,7	703,6

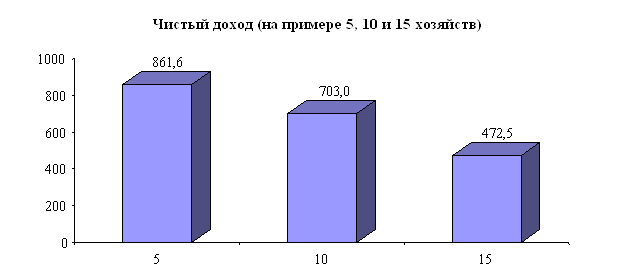
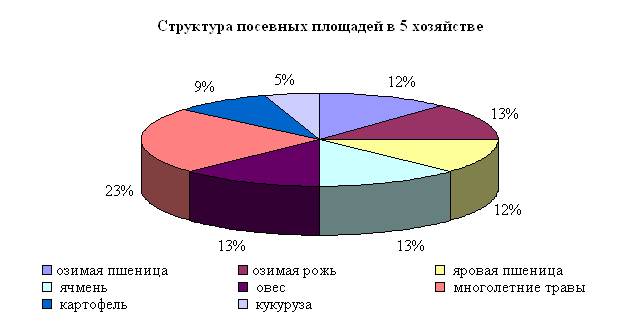
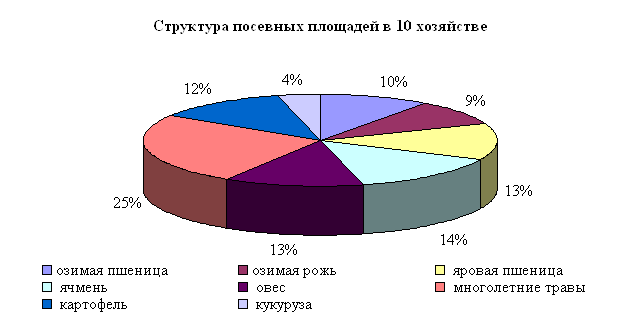
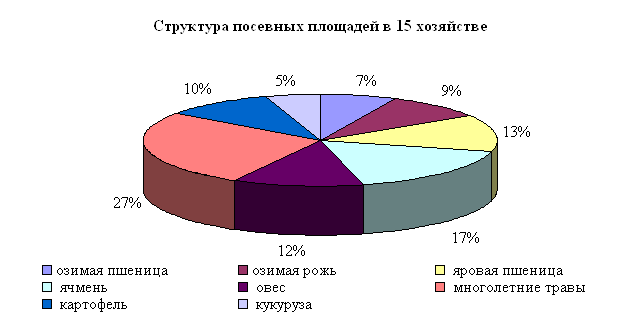
Таблица 8.1.1

Группировка хозяйств района по урожайности озимой пшеницы

(первичная)

№№ групп	Урожайность	Количество хозяйств в группе	Производственные затраты	Затраты удобрений, ц. д. в
I	15,0-18,7	8	246,1	1,91
II	18,8-22,4	5	285,5	2,09
III	22,5-26,1	4	296,5	2,40
IV	26,2-29,8	1	335,6	2,79
V	29,9-33,5	2	327,8	3,12
среднее	21,1	20	278,7	2,22

Таблица 8.1.1.а

Группировка хозяйств района по урожайности озимой пшеницы

(вторичная)

№№ групп	Урожайность	Количество хозяйств в группе	Производственные затраты	Затраты удобрений, ц. д. в
I	15,0-17,0	4	240,3	1,87
II	17,1-19,0	5	258,2	1,96
III	19,1-22,0	4	286,0	2,11
IV	22,1-25,0	4	296,5	2,40
V	25,1-33,5	3	330,4	3,01
среднее	21,1	20	278,7	2,22

Таблица 8.1.2

Группировка хозяйств района по урожайности озимой ржи

(первичная)

№№ групп	Урожайность	Количество хозяйств в группе	Производственные затраты	Затраты удобрений, ц. д. в
I	10,0-15,2	1	217,7	1,84
II	15,3-20,4	4	247,4	1,89
III	20,5-25,5	5	260,6	1,98
IV	25,6-30,7	4	302,8	2,19
V	30,8-35,8	6	308,6	2,71
среднее	25,6	20	278,7	2,22

Таблица 8.1.2.а

Группировка хозяйств района по урожайности озимой ржи

(вторичная)

№№ групп	Урожайность	Количество хозяйств в группе	Производственные затраты	Затраты удобрений, ц. д. в
I	10,0-20,0	4	240,3	1,87
II	20,1-25,0	5	258,2	1,96
III	25,1-30,0	4	286,0	2,11
IV	30,1-33,0	4	296,5	2,40
V	33,1-35,8	3	330,4	3,01
среднее	25,6	20	278,7	2,22

Таблица 8.1.3

Группировка хозяйств района по урожайности яровой пшеницы

(первичная)

№№ групп	Урожайность	Количество хозяйств в группе	Производственные затраты	Затраты удобрений, ц. д. в
I	12,4-15,1	4	240,3	1,87
II	15,2-17,8	3	267,2	1,93
III	17,9-20,5	6	272,2	2,07
IV	20,6-23,2	5	304,3	2,47
V	23,3-26,0	2	327,8	3,12
среднее	19,0	20	278,7	2,22

Таблица 8.1.3.а

Группировка хозяйств района по урожайности яровой пшеницы

(вторичная)

№№ групп	Урожайность	Количество хозяйств в группе	Производственные затраты	Затраты удобрений, ц. д. в
I	12,4-15,0	4	240,3	1,87
II	15,1-18,0	5	258,2	1,96
III	18,1-20,0	4	286,0	2,11
IV	20,1-22,0	3	295,2	2,36
V	22,1-26,0	4	322,9	2,88
среднее	19,0	20	278,7	2,22

Таблица 8.1.4

Группировка хозяйств района по урожайности ячменя

(первичная)

№№ групп	Урожайность	Количество хозяйств в группе	Производственные затраты	Затраты удобрений, ц. д. в
I	10,3-13,3	3	232,2	1,86
II	13,4-16,3	4	266,6	1,92
III	16,4-19,3	6	272,2	2,07
IV	19,4-22,3	5	304,3	2,47
V	22,4-25,2	2	327,8	3,12
среднее	17,5	20	278,7	2,22

Таблица 8.1.4.а

Группировка хозяйств района по урожайности ячменя

(вторичная)

№№ групп	Урожайность	Количество хозяйств в группе	Производственные затраты	Затраты удобрений, ц. д. в
I	10,3-15,0	4	240,3	1,87
II	15,1-17,0	5	258,2	1,96
III	17,1-19,0	4	286,0	2,11
IV	19,1-21,0	4	296,5	2,40
V	21,1-25,2	3	330,4	3,01
среднее	17,5	20	278,7	2,22

Таблица 8.1.5

Группировка хозяйств района по урожайности овса

(первичная)

№№ групп	Урожайность	Количество хозяйств в группе	Производственные затраты	Затраты удобрений, ц. д. в
I	11,2-13,8	2	230,4	1,84
II	13,9-16,4	2	250,2	1,90
III	16,5-19,0	3	267,2	1,93
IV	19,1-21,6	7	279,8	2,11
V	21,7-24,2	6	308,6	2,71
среднее	19,5	20	278,7	2,22

Таблица 8.1.5.а

Группировка хозяйств района по урожайности овса

(вторичная)

№№ групп	Урожайность	Количество хозяйств в группе	Производственные затраты	Затраты удобрений, ц. д. в
I	11,2-17,0	4	240,3	1,87
II	17,1-20,0	5	258,2	1,96
III	20,1-21,0	4	286,0	2,11
IV	21,1-23,0	4	296,5	2,40
V	23,1-24,2	3	330,4	3,01
среднее	19,5	20	278,7	2,22

Таблица 8.1.6

Группировка хозяйств района по урожайности многолетних трав

(первичная)

№№ групп	Урожайность	Количество хозяйств в группе	Производственные затраты	Затраты удобрений, ц. д. в
I	9,0-13,1	7	251,8	1,90
II	13,2-17,2	2	244,7	2,00
III	17,3-21,4	4	286,0	2,11
IV	21,5-25,5	2	302,7	2,35
V	25,6-29,6	5	314,3	2,78
среднее	17,9	20	278,7	2,22

Таблица 8.1.6.а

Группировка хозяйств района по урожайности многолетних трав

(вторичная)

№№ групп	Урожайность	Количество хозяйств в группе	Производственные затраты	Затраты удобрений, ц. д. в
I	9,0-10,0	4	240,3	1,87
II	10,1-15,0	4	251,8	1,95
III	15,1-20,0	4	288,5	2,07
IV	20,1-26,0	5	291,9	2,35
V	26,1-29,6	3	330,4	3,01
среднее	17,9	20	278,7	2,22

Таблица 8.1.7

Группировка хозяйств района по урожайности картофеля

(первичная)

№№ групп	Урожайность	Количество хозяйств в группе	Производственные затраты	Затраты удобрений, ц. д. в
I	125,0-160,0	7	251,8	1,90
II	160,1-195,0	4	259,9	2,02
III	195,1-230,0	2	296,7	2,18
IV	230,1-265,0	2	302,7	2,35
V	265,1-300,0	5	314,3	2,78
среднее	198,4	20	278,7	2,22

Таблица 8.1.7.а

Группировка хозяйств района по урожайности картофеля

(вторичная)

№№ групп	Урожайность	Количество хозяйств в группе	Производственные затраты	Затраты удобрений, ц. д. в
I	125,0-130,0	4	240,3	1,87
II	130,1-170,0	4	251,8	1,95
III	171,1-200,0	3	278,0	2,03
IV	200,1-250,0	4	299,7	2,27
V	250,1-300,0	5	314,3	2,78
среднее	198,4	20	278,7	2,22

Таблица 8.1.8

Группировка хозяйств района по урожайности кукурузы

(первичная)

№№ групп	Урожайность	Количество хозяйств в группе	Производственные затраты	Затраты удобрений, ц. д. в
I	80,0-106,0	4	240,3	1,87
II	106,1-132,0	3	267,2	1,93
III	132,1-158,0	4	259,9	2,02
IV	158,1-184,0	4	299,7	2,27
V	184,1-210,0	5	314,3	2,78
среднее	148,3	20	278,7	2,22

Таблица 8.1.8.а

Группировка хозяйств района по урожайности кукурузы

(вторичная)

№№ групп	Урожайность	Количество хозяйств в группе	Производственные затраты	Затраты удобрений, ц. д. в
I	80,0-110,0	4	240,3	1,87
II	110,1-140,0	4	251,8	1,95
III	140,1-170,0	5	285,5	2,09
IV	170,1-190,0	4	296,5	2,40
V	190,1-210,0	3	330,4	3,01
среднее	148,3	20	278,7	2,22

Таблица 8.2

Группировка хозяйств района по валовой продукции

сельского хозяйства (тыс. руб. на 1 га)

(первичная)

№№ групп	Валовая продукция	Количество хозяйств в группе	Производственные затраты	Размер основных производ. фондов
I	544,2-735,4	6	234,8	1366
II	735,5-926,6	4	275,2	1420
III	926,7-1117,8	2	283,1	1550
IV	1117,9-1309,0	5	301,1	1666
V	1309,1-1500,1	3	330,4	1925
среднее	982,3	20	278,7	1554,0

Таблица 8.2.а

Группировка хозяйств района по валовой продукции

сельского хозяйства (тыс. руб. на 1 га)

(первичная)

№№ групп	Валовая продукция	Количество хозяйств в группе	Производственные затраты	Размер основных производ. фондов
I	544,2-700,0	4	225,5	1356
II	700,1-910,0	4	252,7	1402
III	910,1-1100,0	4	290,8	1485
IV	1100,1-1250,0	4	295,1	1687
V	1250,1-1500,1	4	329,1	1840
среднее	982,3	20	278,7	1554,0

Таблица 9.1

Группировка хозяйств района по урожайности озимой пшеницы

(комбинированная)

№№ групп	Группы по урожайности с 1 га	Подгруппы по баллу бонитета почв	Число хозяйств в группе	Затраты удобрений, ц. д. в.
I	15,0-18,7	37,0-67,5 67,6-98,0	4 4	1,89 1,93
	итого по группе		8	1,91
II	18,8-22,4	37,0-67,5 67,6-98,0	3 2	2,07 2,11
	итого по группе		5	2,09
III	22,5-26,1	37,0-67,5 67,6-98,0	2 2	2,42 2,37
	итого по группе		4	2,40
IV	26,2-29,8	37,0-67,5 67,6-98,0	1 -	2,37 -
	итого по группе		1	2,79
V	29,9-33,5	37,0-67,5 67,6-98,0	- 2	- 3,12
	итого по группе		2	3,12
среднее	21,1	69,0	20	2,22

Таблица 9.2

Группировка хозяйств района по урожайности озимой ржи

(комбинированная)

№№ групп	Группы по урожайности с 1 га	Подгруппы по баллу бонитета почв	Число хозяйств в группе	Затраты удобрений, ц. д. в.
I	10,0-15,2	37,0-67,5 67,6-98,0	1 -	1,84 -
	итого по группе		1	1,84
II	15,3-20,4	37,0-67,5 67,6-98,0	2 2	1,89 1,90
	итого по группе		4	1,89
III	20,5-25,5	37,0-67,5 67,6-98,0	3 2	1,99 1,97
	итого по группе		5	1,98
IV	25,6-30,7	37,0-67,5 67,6-98,0	2 2	2,27 2,11
	итого по группе		4	2,19
V	30,8-35,8	37,0-67,5 67,6-98,0	2 4	2,64 2,74
	итого по группе		6	2,71
среднее	25,6	69,0	20	2,22

Таблица 9.3

Группировка хозяйств района по урожайности яровой пшеницы

(комбинированная)

№№ групп	Группы по урожайности с 1 га	Подгруппы по баллу бонитета почв	Число хозяйств в группе	Затраты удобрений, ц. д. в.
I	12,4-15,1	37,0-67,5 67,6-98,0	2 2	1,84 1,90
	итого по группе		4	187
II	15,2-17,8	37,0-67,5 67,6-98,0	2 1	1,93 1,93
	итого по группе		3	1,93
III	17,9-20,5	37,0-67,5 67,6-98,0	3 3	2,07 2,07
	итого по группе		6	2,07
IV	20,6-23,2	37,0-67,5 67,6-98,0	3 2	2,54 2,37
	итого по группе		5	2,47
V	23,3-26,0	37,0-67,5 67,6-98,0	- 2	- 3,12
	итого по группе		2	3,12
среднее	19,0	69,0	20	2,22

Таблица 9.4

Группировка хозяйств района по урожайности ячменя

(комбинированная)

№№ групп	Группы по урожайности с 1 га	Подгруппы по баллу бонитета почв	Число хозяйств в группе	Затраты удобрений, ц. д. в.
I	10,3-13,3	37,0-67,5 67,6-98,0	2 1	1,84 1,90
	итого по группе		3	1,86
II	13,4-16,3	37,0-67,5 67,6-98,0	2 2	1,93 1,92
	итого по группе		4	1,92
III	16,4-19,3	37,0-67,5 67,6-98,0	3 3	2,07 2,07
	итого по группе		6	2,07
IV	19,4-22,3	37,0-67,5 67,6-98,0	3 2	2,54 2,37
	итого по группе		5	2,47
V	22,4-25,2	37,0-67,5 67,6-98,0	- 2	- 3,12
	итого по группе		2	3,12
среднее	17,5	69,0	20	2,22

Таблица 9.5

Группировка хозяйств района по урожайности овса

(комбинированная)

№№ групп	Группы по урожайности с 1 га	Подгруппы по баллу бонитета почв	Число хозяйств в группе	Затраты удобрений, ц. д. в.
I	11,2-13,8	37,0-67,5 67,6-98,0	2 -	1,84 -
	итого по группе		2	1,84
II	13,9-16,4	37,0-67,5 67,6-98,0	- 2	- 1,90
	итого по группе		2	1,90
III	16,5-19,0	37,0-67,5 67,6-98,0	2 1	1,93 1,93
	итого по группе		3	1,93
IV	19,1-21,6	37,0-67,5 67,6-98,0	4 3	2,14 2,07
	итого по группе		7	2,11
V	21,7-24,2	37,0-67,5 67,6-98,0	2 4	2,64 2,74
	итого по группе		6	2,71
среднее	19,5	69,0	20	2,22

Таблица 9.6

Группировка хозяйств района по урожайности многолетние травы

(комбинированная)

№№ групп	Группы по урожайности с 1 га	Подгруппы по баллу бонитета почв	Число хозяйств в группе	Затраты удобрений, ц. д. в.
I	9,0-13,1	37,0-67,5 67,6-98,0	4 3	1,89 1,91
	итого по группе		7	1,90
II	13,2-17,2	37,0-67,5 67,6-98,0	1 1	2,00 2,00
	итого по группе		2	2,00
III	17,3-21,4	37,0-67,5 67,6-98,0	2 2	2,11 2,11
	итого по группе		4	2,11
IV	21,5-25,5	37,0-67,5 67,6-98,0	1 1	2,35 2,35
	итого по группе		2	2,35
V	25,5-29,6	37,0-67,5 67,6-98,0	2 3	2,64 2,87
	итого по группе		5	2,78
среднее	17,9	69,0	20	2,22

Таблица 9.7

Группировка хозяйств района по урожайности картофеля

(комбинированная)

№№ групп	Группы по урожайности с 1 га	Подгруппы по баллу бонитета почв	Число хозяйств в группе	Затраты удобрений, ц. д. в.
I	125,0-160,0	37,0-67,5 67,6-98,0	4 3	1,89 1,91
	итого по группе		7	1,90
II	160,1-195,0	37,0-67,5 67,6-98,0	2 2	2,02 2,02
	итого по группе		4	2,02
III	195,1-230,0	37,0-67,5 67,6-98,0	1 1	2,18 2,18
	итого по группе		2	2,18
IV	230,1-265,0	37,0-67,5 67,6-98,0	1 1	2,35 2,35
	итого по группе		2	2,35
V	265,1-300,0	37,0-67,5 67,6-98,0	2 3	2,64 2,87
	итого по группе		5	2,78
среднее	198,4	69,0	20	2,22

Таблица 9.8

Группировка хозяйств района по урожайности кукурузы

(комбинированная)

№№ групп	Группы по урожайности с 1 га	Подгруппы по баллу бонитета почв	Число хозяйств в группе	Затраты удобрений, ц. д. в.
I	80,0-106,0	37,0-67,5 67,6-98,0	2 2	1,84 1,90
	итого по группе		4	187
II	106,1-132,0	37,0-67,5 67,6-98,0	2 1	1,93 1,93
	итого по группе		3	1,93
III	132,1-158,0	37,0-67,5 67,6-98,0	2 2	2,02 2,02
	итого по группе		4	2,02
IV	158,1-184,0	37,0-67,5 67,6-98,0	2 2	2,27 2,27
	итого по группе		4	2,27
V	184,1-210,0	37,0-67,5 67,6-98,0	2 3	2,64 2,87
	итого по группе		5	2,78
среднее	148,3	69,0	20	2,22

Таблица 10

Аналитическая группировка хозяйств района

по величине чистого дохода в растениеводстве (тыс. руб. на 1 га)

№№ групп	Чистый доход	Количество хозяйств в группе	Валовая продукция	Производственные затраты	Основные производственные фонды	Затраты живого труда, чел/час	Затраты удобрений, ц. д. в./га
I	326,6-494,0	6	654,4	234,8	1365,7	61,5	1,90
II	494,1-661,5	4	873,2	275,2	1420,0	77,5	1,98
III	661,6-829,0	3	1051,1	295,3	1558,7	95,7	2,13
IV	829,1-996,5	4	1185,5	296,5	1688,5	106,5	2,40
V	свыше 996,5	3	1443,7	330,4	1925,0	142,3	3,01
среднее	703,6	20	982,3	287,7	1554,0	91,0	2,22