
Рефераты по рекламе
Рефераты по физике
Рефераты по философии
Рефераты по финансам
Рефераты по химии
Рефераты по хозяйственному праву
Рефераты по экологическому праву
Рефераты по экономико-математическому моделированию
Рефераты по экономической географии
Рефераты по экономической теории
Рефераты по этике
Рефераты по юриспруденции
Рефераты по языковедению
Рефераты по юридическим наукам
Рефераты по истории
Рефераты по компьютерным наукам
Рефераты по медицинским наукам
Рефераты по финансовым наукам
Рефераты по управленческим наукам
Психология педагогика
Промышленность производство
Биология и химия
Языкознание филология
Издательское дело и полиграфия
Рефераты по краеведению и этнографии
Рефераты по религии и мифологии
Рефераты по медицине
Контрольная работа: Математические методы и модели в экономике
Контрольная работа: Математические методы и модели в экономике
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
КАМСКАЯ ГОСУДАРСТВЕННАЯ ИНЖЕНЕРНО-ЭКОНОМИЧЕСКАЯ АКАДЕМИЯ
КАФЕДРА ЭОУП
КОНТРОЛЬНАЯ РАБОТА
по дисциплине "Математические методы и модели в экономике"
Выполнил: студент гр. 4381-С
Кустовский Р.Г.
Проверил: доцент
Коврижных О.Е.
г. Набережные Челны
2010
ЗАДАНИЕ 1
Построить одноиндексную математическую модель задачи линейного программирования. В модели надо указать единицы измерения всех переменных, целевой функции и каждого ограничения
Цех мебельного комбината выпускает трельяжи, трюмо и тумбочки под телевизоры. Норма расхода материала в расчете на одно изделие, плановая себестоимость, оптовая цена предприятия, плановый ассортимент и трудоемкость единицы продукции приведены в таблице. При этом, запас древесно-стружечных плит, досок еловых и березовых 92, 33 и 17 куб.м. соответственно. Плановый фонд рабочего времени 19100 человеко-часов.
Исходя из необходимости выполнения плана по ассортименту и возможности его перевыполнения по отдельным (и даже всем) показателям, постройте модель, на основе которой можно найти план производства, максимизирующий прибыль.
| Показатели | Изделия | ||
| трельяж | трюмо | тумбочка | |
| Норма расхода материала, куб.м.: | |||
| древесно-стружечные плиты | 0,042 | 0,037 | 0,028 |
| доски еловые | 0,024 | 0,018 | 0,081 |
| доски березовые | 0,007 | 0,008 | 0,005 |
| Трудоемкость, чел.-ч. | 7,5 | 10,2 | 6,7 |
| Плановая себестоимость, ден.ед. | 98,81 | 65,78 | 39,42 |
| Оптовая цена предприятия, ден.ед. | 97,10 | 68,20 | 31,70 |
| Плановый ассортимент, шт. | 450 | 1200 | 290 |
Решение:
В условии задачи сформулирована цель получение максимальной прибыли при необходимости выполнения плана по ассортименту и возможности его перевыполнения. Поэтому, искомыми величинами, а значит, и переменными задачи являются количество произведенной продукции:
Х1 - количество изготовленных трельяжей.
Х2 - количество изготовленных трюмо.
Х3 - количество изготовленных тумбочек.
Поэтому целевой функцией будет математическое выражение, в которой суммируется прибыль от изготовления каждой продукции. Прибыль является разность между себестоимостью и оптовой ценой продукции.
L = (97,10 – 98,81) *Х1 + (68,2 – 65,78)* Х2 +(31,7 – 39,42)* Х3 =
= –1,71 * Х1+ 2,42 * Х2 – 7,72 * Х3 àmax
Условием является то, что сумма расхода материалов не должно быть больше имеющихся материалов, а так же обязательное условие - выполнение плана. Таким образом, математическая модель задачи будет иметь вид:
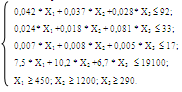
ЗАДАНИЕ 2
Решить одноиндексную задачу линейного программирования графическим методом.

Построим следующие прямые:
х1 + х2 = 2 (1)
-х1 + х2 = 4 (2)
х1 + 2х2 = 8 (3)
х1 = 6 (4)
Для этого вычислим координаты прямых:

Заштрихуем полуплоскости, определяемые и разрешаемые каждым из ограничений неравенств. Определим область допустимых решений , многоугольник АВCDEF.
Построим целевую функцию по уравнению

Нижняя точка пересечения целевой функции и многоугольника – это точка минимума целевой функции.
Найдем координаты точки D ( 2; 0 ).
Минимальное значение целевой функции
L(Х) = L(D) = 1*2 + 3*0 = 2
ЗАДАНИЕ 3
Задача сетевого планирования
По данным варианта необходимо:
1) построить сетевую модель, рассчитать временные параметры событий (на рисунке) и работ (в таблице);
2) определить критические пути модели;
3) оптимизировать сетевую модель по критерию "минимум исполнителей" (указать какие работы надо сдвигать и на сколько дней, внесенные изменения показать на графиках привязки и загрузки пунктирной линией).
|
Название работы |
Нормальная длительность |
Количество исполнителей |
Вариант 2 (N=11 человек)1. D - исходная работа проекта; 2. Работа E следует за D; 3. Работы A, G и C следуют за E; 4. Работа B следует за A; 5. Работа H следует за G; 6. Работа F следует за C; Работа I начинается после завершения B, H, и F |
| A | 3 | 5 | |
| B | 4 | 7 | |
| C | 1 | 1 | |
| D | 4 | 3 | |
| E | 5 | 2 | |
| F | 7 | 3 | |
| G | 6 | 6 | |
| H | 5 | 1 | |
| I | 8 | 5 |
1. Построим сетевую модель, рассчитаем временные параметры событий ( на рисунке) и работ ( в таблице).
Сетевой график
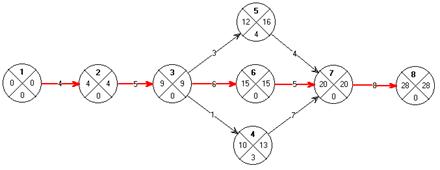
| Код | Название работы | t | Трн | Тро | Тпн | Тпо | Rп | Rс |
| 1-2 | D | 4 | 0 | 4 | 0 | 4 | 0 | 0 |
| 2-3 | E | 5 | 4 | 9 | 4 | 9 | 0 | 0 |
| 3-5 | A | 3 | 9 | 12 | 13 | 16 | 4 | 0 |
| 3-6 | G | 6 | 9 | 15 | 9 | 15 | 0 | 0 |
| 3-4 | C | 1 | 9 | 10 | 12 | 13 | 3 | 0 |
| 5-7 | B | 4 | 12 | 16 | 16 | 20 | 4 | 4 |
| 6-7 | H | 5 | 15 | 20 | 15 | 20 | 0 | 0 |
| 4-7 | F | 7 | 10 | 17 | 13 | 20 | 3 | 3 |
| 7-8 | I | 8 | 20 | 28 | 20 | 28 | 0 | 0 |
В таблице использованы следующие сокращения:
t - длительность работы
Трн - ранний срок начала работы
Тро - ранний срок окончания работы
Тпн - поздний срок начала работы
Тпо - ранний срок окончания работы
Rп - полный резерв времени
Rс - свободный резерв времени
2. Определим критические пути модели
Критический путь – 1,2,3,6,7,8 = 28 суток - максимальный по продолжительности полный путь.
3. Оптимизируем сетевую модель по критерию "минимум исполнителей" (укажем какие работы надо сдвигать и на сколько дней, внесенные изменения показать на графиках привязки и загрузки пунктирной линией).
Построим график привязки для следующих исходных данных.
| Название работы |
|
|
Количество исполнителей |
| D | 1-2 | 4 | 3 |
| E | 2-3 | 5 | 2 |
| A | 3-5 | 3 | 5 |
| G | 3-6 | 6 | 6 |
| C | 3-4 | 1 | 1 |
| B | 5-7 | 4 | 7 |
| H | 6-7 | 5 | 1 |
| F | 4-7 | 7 | 3 |
| I | 7-8 | 8 | 5 |
При оптимизации использования ресурса рабочей силы сетевые работы чаще всего стремятся организовать таким образом, чтобы:
· количество одновременно занятых исполнителей было минимальным;
· выровнять потребность в людских ресурсах на протяжении срока выполнения проекта.
Проведенная оптимизация была основана на использовании свободных и полных резервов работ.
Для этого необходимо чуть дальше сдвинуть указанные работы, а именно: работу (3,5) сдвинуть на 1 дней, работу (5,7) - на 3 дня, и работу (4,7) на 3 дня.
В результате оптимизации количество одновременно занятых исполнителей снизили с 16 человек до 11.
ЗАДАНИЕ 4
Решить задачу управления запасами.
Завод радиоэлектронной аппаратуры производит 860 радиоприемников в сутки. Микросхемы для радиоприемников (по 1 шт. на приемник) производятся на этом же заводе с интенсивностью 3420 тыс. шт. в сутки. Затраты на подготовку производства партии микросхем составляют 81 руб. (числа в задаче условные), себестоимость производства 1 тыс. шт. микросхем равна 25 руб. Хранение микросхем на складе обходится заводу в 1,5 руб. за каждую тысячу в сутки. У завода появилась возможность закупать микросхемы в другом месте по цене 25 руб. за 1 тыс. шт. Стоимость доставки равна 32 руб.
Выясните, стоит ли заводу закупать микросхемы вместо того, чтобы их производить. Для более выгодного режима работы завода (производство или закупка) определите периодичность подачи заказа, и затраты на управление запасами в месяц (22 рабочих дня).
1. Для моделирования процессов производства продукции применим модель планирования экономичного размера партии.
Размер партии микросхем, производимых на заводе:
Q* = Ö (2К1*n*l)/(S(l-n)
Q* = Ö (2*81*0,86*3420) /(1,5*(3420 – 0,86) = 9,639 тыс. шт.
Частота запуска микросхем в производство:
t1=(Q*/n)*q
t1= (9,639/0,86)*22 = 246,6 часов ~ 4,1 ~ 4 рабочих дней
Общие затраты на управление запасами:
L1 = К1*(n/Q*) + S*( Q*(l - n))/(2l) + Сin
L1 = 81*(0,860/9,639) + 1,5* (9,639*(3420 – 0,86))/(2*3420) + 25*0,86 = 36 руб/сут.
L1 = 36 *22 = 792 руб/мес.
2. Моделирование процесса закупки произведем с помощью модели Уилсона.
Размер партии заказа:
Qw = Ö2*К2n/S
Qw = Ö2*32*0,86/1,5= 6,057 тыс. шт
Подача каждого нового заказа должна производиться через:
t2 = (Qw/n)*q
t2 = (6,057/0,86)*22 = 154,946 часов ~ 5,16 ~ 5 раб. дней
Затраты на управление запасами:
L2 = К2*(n/Q) + S*(Q/2) + С2n
L2 = 32*(0,86/6,057) + 1,5*(6,057/2) + 25*0,86 = 30,6 руб./сут
L2 = 30,6 *22 = 672,9 руб./мес.
Ответ: таким образом, можно сделать вывод, что заводу выгодно покупать микросхемы у внешнего источника, чем производить их самим, расходы в этом случае меньше.