Контрольная работа: Линейные уравнения парной и множественной регрессии

НЕГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

"ВОЛГОГРАДСКИЙ ИНСТИТУТ БИЗНЕСА"

Кафедра

Математики и естественных наук

Домашняя контрольная работа

Дисциплина

Эконометрика

Тема: Линейные уравнения парной регрессии

Студента (ки)

Иванова Ивана Ивановича

Волгоград 2010

Задача№ 1

По данным приведенным в таблице:

1) построить линейное уравнение парной регрессии y на x;

2) рассчитать линейный коэффициент парной корреляции и оценить тесноту связи;

3) оценить статистическую значимость параметров регрессии и корреляции, используя F-статистику, t-статистику Стьюдента и путем расчета доверительных интервалов каждого из показателей;

4) вычислить прогнозное значение y при прогнозном значении x, составляющем 108% от среднего уровня.

5) оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал;

6) полученные результаты изобразить графически и привести экономическое обоснование.

Таблица №1

По территориям Центрального района известны данные за 1995 г.

Район	Средний размер назначенных ежемесячных пенсий, тыс.руб., y	Прожиточный минимум в среднем на одного пенсионера в месяц, тыс.руб., х
Брянская обл.	240	178
Владимирская обл.	226	202
Ивановская обл.	221	197
Калужская обл.	226	201
Костромская обл.	220	189
Московская обл.	237	215
Орловская обл.	232	166
Рязанская обл.	215	199
Смоленская обл.	220	180
Тульская обл.	231	186
Ярославская обл.	229	250

xi	178	202	197	201	189	215	166	199	180	186	250
yi	240	226	221	226	220	237	232	215	220	231	229

Х	Y
178	240
202	226
197	221
201	226
189	220
215	237
166	232
199	215
180	220
186	231
250	229

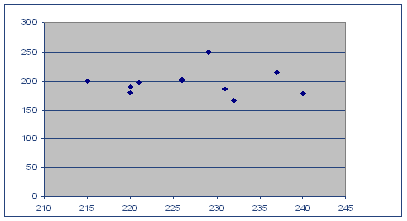
Вывод 1. Анализ корреляционного поля данных показывает, что между признаками и в выборочной совокупности существует прямая и достаточно тесная связь. Предполагается, что объясняемая переменная линейно зависит от фактора , поэтому уравнение регрессии будем искать в виде

Таблица № 4 Параметры (коэффициенты) уравнения регрессии

	Коэффициенты
Y-пересечение	227,7117993
Переменная X 1	-0,003619876

На основании этих данных запишем уравнение регрессии: .

Коэффициент называется выборочным коэффициентом регрессии Коэффициент регрессии показывает, на сколько единиц в среднем изменяется переменная при увеличении переменной на одну единицу.

Таблица №5. Корреляционная матрица

	Столбец 1	Столбец 2
Столбец 1	1
Столбец 2	-0,010473453	1

Для оценки качества уравнения регрессии в целом необходимо проверить статистическую значимость индекса детерминации: проверяется нулевая гипотеза , используется .

Таблица №6

Регрессионная статистика
R-квадрат		0,000109693

Т.к. Значение детерминации R-квадрат имеет малое значение, которое менее 1%, то дальнейшее решение не имеет смысла, т.к. вероятность того что прогноз будет верным меньше 1%.

Задача №2

Используя данные, приведенные в таблице: построить линейное уравнение множественной регрессии;

1) оценить значимость параметров данного уравнения и построить доверительные интервалы для каждого из параметров, оценить значимость уравнения в целом, пояснить экономический смысл полученных результатов;

2) рассчитать линейные коэффициенты частной корреляции и коэффициент множественной детерминации, сравнить их с линейными коэффициентами парной корреляции, пояснить различия между ними;

3) вычислить прогнозное значение y при уменьшении вектора x на 6 % от максимального уровня, оценить ошибку прогноза и построить доверительный интервал прогноза;

Таблица №5

номер наблюдения, i	Накопления семьи, Y (y.e.)	Доход семьи, X1 (y.e.)	Расходы на питание, X 2 (y.e.)
1	2	20	5
2	6	27	6
3	7	26	7
4	5	19	5
5	4	15	5
6	2	15	5
7	7	28	10
8	6	24	7
9	4	14	6
10	5	21	7
11	5	20	10
12	3	18	6

Таблица №6 Параметры (коэффициенты) уравнения регрессии

	Коэффициенты
Y-пересечение	-1,767785782
x1	0,232792618
x2	0,24953991

Множественная регрессия широко используется в решении проблем спроса, доходности акций, изучении функции издержек производства, в макроэкономических расчетах и целого ряда других вопросов эконометрики. В настоящее время множественная регрессия - один из наиболее распространенных методов в эконометрике. Основная цель множественной регрессии - построить модель с большим числом факторов, определив при этом влияние каждого из них в отдельности, а также совокупное их воздействие на моделируемый показатель.

На основании этих данных запишем уравнение регрессии:

Таблица №7 Регрессионная статистика

R-квадрат	0,663668925
Нормированный R-квадрат	0,588928686

! Параметр R-квадрат, представляет собой квадрат коэффициента корреляции rxy2 и называется коэффициентом детерминации. Величина данного коэффициента характеризует долю дисперсии зависимой переменной y, объясненную регрессией (объясняющей переменной x). Соответственно величина 1 - rxy2 характеризует долю дисперсии переменной y, вызванную влиянием всех остальных, неучтенных в эконометрической модели объясняющих переменных. Доля всех неучтенных в полученной эконометрической модели объясняющих переменных приблизительно составляет: 0,663668, или 66,3%.

Находим, что численное значение , а скорректированный (нормированный, исправленный) коэффициент детерминации равен

1) Для оценки качества уравнения регрессии в целом необходимо проверить статистическую значимость индекса детерминации : проверяется нулевая гипотеза , используется .

Наблюдаемое значение критерия и оценку его значимости находим в Таблице №8

Таблица №8 Дисперсионный анализ:

F	Значимость F
8,87967358	0,007420813

! Включаемые в уравнение множественной регрессии факторы должны объяснить вариацию зависимой переменной. Если строится модель с некоторым набором факторов, то для нее рассчитывается показатель детерминации, который фиксирует долю объясненной вариации результативного признака (объясняемой переменной) за счет рассматриваемых в регрессии факторов. А оценка влияния других, неучтенных в модели факторов, оценивается вычитанием из единицы коэффициента детерминации, что и приводит к соответствующей остаточной дисперсии.

Таким образом, при дополнительном включении в регрессию еще одного фактора коэффициент детерминации должен возрастать, а остаточная дисперсия уменьшаться. Если этого не происходит и данные показатели практически недостаточно значимо отличаются друг от друга, то включаемый в анализ дополнительный фактор не улучшает модель и практически является лишним фактором.

Если модель насыщается такими лишними факторами, то не только не снижается величина остаточной дисперсии и не увеличивается показатель детерминации, но, более того, снижается статистическая значимость параметров регрессии по критерию Стьюдента вплоть до статистической незначимости.

2) Для статистической оценки значимости коэффициентов регрессии () используем статистику Стьюдента.

Проверяется нулевая гипотеза .

Для проверки нулевой гипотезы необходимо знать величину наблюдаемых значений критерия . Их значения и оценки их статистической значимости найдем в Таблице №9

Таблица №9

t-статистика	P-Значение
-1,127971079	0,28850322
2,838964459	0,01943598
1,130728736	0,28740002

В этой же таблице находим границы доверительных интервалов для каждого из параметров:

Нижние 95%	Верхние 95%
-5,313097658	1,777526094
0,047297697	0,418287538
-0,249694323	0,748774142

3. Значения парных коэффициентов корреляции найдем из соответствующей матрицы.

Таблица №10 Корреляционная матрица

	y	x1	x2
y	1
x1	0,784786247	1
x2	0,60206001	0,531178469	1

По величине парных коэффициентов корреляции может обнаруживаться лишь явная коллинеарность факторов. Наибольшие трудности в использовании аппарата множественной регрессии возникают при наличии мультиколлинеарности факторов, когда более чем два фактора связаны между собой линейной зависимостью, т.е. имеет место совокупное воздействие факторов друг на друга.

Наличие мультиколлинеарности факторов может означать, что некоторые факторы будут всегда действовать в унисон. В результате вариация в исходных данных перестает быть полностью независимой и нельзя оценить воздействие каждого фактора в отдельности. Чем сильнее мультиколлинеарность факторов, тем менее надежна оценка распределения суммы объясненной вариации по отдельным факторам с помощью метода наименьших квадратов (МНК).

Частные коэффициенты корреляции найдем по формулам

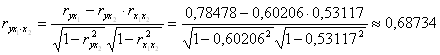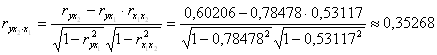их значения показывают, что при отсутствии влияния других факторов, связь с рассматриваемым фактором усиливается т.е. мультиколлинеарность между ними существует.

4. Рассчитаем прогнозное значение результата, если прогнозные значения факторов составляют 110% их максимального значения. Найдем прогнозные значения факторов и подставим их в полученное уравнение регрессии.

По условию прогнозные значения составляют 110% их максимального значения.

Таблица №11

maxX1	maxX2
28	10

Далее вычисляем прогнозные значения факторов: . Затем, подставив эти значения в уравнение регрессии, получим прогнозное (предсказанное) значение фактора . Доверительный интервал прогноза оценивается формулой: , где - ошибка прогноза,стандартная ошибка регрессии.

Таблица №12

Стандартная ошибка

1,104878833

;

- коэффициент Стьюдента, который в данном случае имеет смысл кратности случайной (стандартной) ошибки прогноза ;

- число, которое получим в результате операций над матрицами:

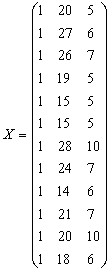матрица значений факторных переменных ,

транспонированная матрица ;

- произведение матриц ;

- матрица, обратная к матрице ;

- матрица прогнозных значений факторов;

- транспонированная матрица прогнозов.

Фактор представляет собой фиктивную переменную, которую необходимо ввести в уравнение регрессии для того, чтобы преобразовать его в "приведенную" форму вида .

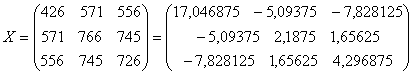
Максимальную ошибку прогноза =11,07714043: 1) нижняя граница прогноза =44,92285957, 2) верхнюю границу прогноза =67,07714043. Интервал прогнозных значений результативного признака

Задача № 3

Используя данные, представленные в таблице проверить наличие гетероскедастичности, применяя тест Голдфельда-Квандта.

Таблица№13. Данные

Страна	Индекс человеческого развития, У	Расходы на конечное потребление в текущих ценах, % к ВВП, Х
Австрия	0,904	75,5
Австралия	0,922	78,5
Англия	0,918	84,4
Белоруссия	0,763	78,4
Бельгия	0,923	77,7
Германия	0,906	75,9
Дания	0,905	76,0
Индия	0,545	67,5
Испания	0,894	78,2
Италия	0,900	78,1
Канада	0,932	78,6
Казахстан	0,740	84,0
Китай	0,701	59,2
Латвия	0,744	90,2
Нидерланды	0,921	72,8
Норвегия	0,927	67,7
Польша	0,802	82,6
Россия	0,747	74,4
США	0,927	83,3
Украина	0,721	83,7
Финляндия	0,913	73,8
Франция	0,918	79,2
Чехия	0,833	71,5
Швейцария	0,914	75,3
Швеция	0,923	79,0

1) Найдем параметры линейного уравнения множественной регрессии и значения остатков.

Определим остаточные суммы квадратов и , то есть суммы квадратов остатков регрессии по "урезанным выборкам".

Таблица№14

№	Y	X	Yp	ei	(ei) ^2
1	0,932	78,6	77,90431365	0,695686352	0,483979501
2	0,927	67,7	77,85057558	-10,15057558	103,0341846
3	0,927	83,3	77,85057558	5,44942442	29,69622651
4	0,923	77,7	77,80758513	-0,107585125	0,011574559
5	0,923	79,0	77,80758513	1, 192414875	1,421853234
6	0,922	78,5	77,79683751	0,703162488	0,494437485
7	0,921	72,8	77,7860899	-4,986089898	24,86109247
8	0,918	84,4	77,75384706	6,646152943	44,17134894	S1
9	0,918	79,2	77,75384706	1,446152943	2,091358334	206,2660556
10	0,914	75,3	77,7108566	-2,410856603	5,812229559
11	0,913	73,8	77,70010899	-3,900108989	15,21085013
12	0,906	75,9	77,62487569	-1,724875694	2,975196159
13	0,905	76,0	77,61412808	-1,61412808	2,60540946
14	0,904	75,5	77,60338047	-2,103380467	4,424209388
15	0,900	78,1	77,56039001	0,539609988	0,291178939
16	0,894	78,2	77,49590433	0,704095669	0,495750712
17	0,833	71,5	76,8402999	-5,3402999	28,51880303
18	0,802	82,6	76,50712388	6,092876121	37,12313943
19	0,763	78,4	76,08796695	2,312033052	5,345496834
20	0,747	74,4	75,91600513	-1,51600513	2,298271555
21	0,744	90,2	75,88376229	14,31623771	204,9546622
22	0,740	84,0	75,84077183	8,159228165	66,57300425
23	0,721	83,7	75,63656718	8,063432824	65,0189489
24	0,701	59,2	75,4216149	-16,2216149	263,1407901	S2
25	0,545	67,5	73,74498718	-6,244987181	38,99986489	743,7878055

1) Находим наблюдаемое значение критерия . По условию задачи . Из таблицы значений Фишера находим, что

Вывод: отвергаем нулевую гипотезу на принятом уровне значимости , т.к. наблюдаемое значение критерия больше табличного.

Следовательно, предположение об однородности дисперсий ошибок, при условии, что выполнены стандартные предположения о модели наблюдений, включая предположение о нормальности ошибок, неверно. Наблюдается гетероскедастичность, что приводит к ошибочным статистическим выводам при использовании МНК. Следовательно, полученные оценки не являются состоятельными.

Задача № 4

По данным таблицы построить уравнение регрессии, выявить наличие автокорреляции остатков, используя критерий Дарбина - Уотсона, и проанализировать пригодность полученного уравнения для построения прогнозов.

Таблица №15

Год	Выпуск продукции в США в среднем за 1 час, % к уровню 1982 г., Х	Среднечасовая заработная плата в экономике США, в сопоставимых ценах 1982 г., Y
1960	65,6	6,79
1961	68,1	6,88
1962	73,3	7,07
1963	76,5	7,17
1964	78,6	7,33
1965	81,0	7,52
1966	83,0	7,62
1967	85,4	7,72
1968	85,9	7,89
1969	85,9	7,98
1970	87,0	8,03
1971	90,2	8,21
1972	92,6	8,53
1973	95,0	8,55
1974	93,3	8,28
1975	95,5	8,12

Найдем параметры линейного уравнения множественной регрессии и значения остатков.

Дополним таблицу данных столбцами "", "Квадрат разности остатков " и "Квадрат остатка " и заполним их.

Таблица №16

Y	X	Yi	et	et-1	(et-et-1) ^2	et^2
6,79	65,6	6,667235239	0,122765			0,015071
6,88	68,1	6,815288112	0,064712	0,122765	0,003370136	0,004188
7,07	73,3	7,123238088	-0,05324	0,064712	0,013912197	0,002834
7,17	76,5	7,312745766	-0,14275	-0,05324	0,008011624	0,020376
7,33	78,6	7,437110179	-0,10711	-0,14275	0,001269895	0,011473
7,52	81,0	7,579240937	-0,05924	-0,10711	0,002291464	0,003509
7,62	83,0	7,697683236	-0,07768	-0,05924	0,000340118	0,006035
7,72	85,4	7,839813994	-0,11981	-0,07768	0,001775001	0,014355
7,89	85,9	7,869424568	0,020575	-0,11981	0,019709191	0,000423
7,98	85,9	7,869424568	0,110575	0,020575	0,008100000	0,012227
8,03	87,0	7,934567833	0,095432	0,110575	0,000229318	0,009107
8,21	90,2	8,12407551	0,085924	0,095432	0,000090396	0,007383
8,53	92,6	8,266206268	0,263794	0,085924	0,031637467	0,069587
8,55	95,0	8,408337026	0,141663	0,263794	0,014915922	0,020068
8,28	93,3	8,307661073	-0,02766	0,141663	0,028670633	0,000765
8,12	95,5	8,437947601	-0,31795	-0,02766	0,084266268	0,101091
				Суммы	0,218589631	0,298494

По формуле вычислим значение статистики :

Так как , то значение статистики

равно .

По таблице критических точек Дарбина Уотсона определим значения критерия Дарбина-Уотсона (нижнее) и (верхнее) для заданного числа наблюдений , числа независимых переменных модели и уровня значимости . Итак, находим, что , .

По этим значениям числовой промежуток разбиваем на пять отрезков:

На основании выполненных расчетов находим, что наблюдаемое значение статистики принадлежит первому интервалу.

Вывод: существует отрицательная автокорреляция, то есть гипотеза отклоняется и с вероятностью принимается гипотеза .

Следовательно, полученное уравнение регрессии не может быть использовано для прогноза, так как в нем не устранена автокорреляция в остатках, которая может иметь разные причины. Автокорреляция в остатках может означать, что в уравнение не включен какой-либо существенный фактор. Возможно также, что форма связи неточна.

Задача № 5

В таблице приводятся данные о динамике выпуска продукции Финляндии (млн. долл.).

Таблица №17

Год	Выпуск продукции, yt млн.долл.
1989	23 298
1990	26 570
1991	23 080
1992	29 800
1993	28 440
1994	29 658
1995	39 573
1996	38 435
1997	39 002
1998	39 020
1999	40 012
2000	41 005
2001	39 080
2002	42 680

Задание:

1. Постройте график временного ряда.

2. Сделайте вывод о присутствии или отсутствии тренда при доверительной вероятности 0,95.

3. Найдите среднее значение, среднеквадратическое отклонение и коэффициенты автокорреляции (для лагов ) заданного ВР.

4. Проведите сглаживание данного ВР методом скользящих средних, используя простую среднюю арифметическую с интервалом сглаживания ;

5. Найдите уравнение тренда ВР , предполагая, что он линейный, и проверьте его значимость на уровне .

6. Дайте точечный и интервальный (с надежностью 0,95) прогнозы индивидуального значения выпуска продукции на 2003 год.

Таблица №18

Год	t	Выпуск продукции, yt млн.долл.
1989	1	23 298
1990	2	26 570
1991	3	23 080
1992	4	29 800
1993	5	28 440
1994	6	29 658
1995	7	39 573
1996	8	38 435
1997	9	39 002
1998	10	39 020
1999	11	40 012
2000	12	41 005
2001	13	39 080
2002	14	42 680

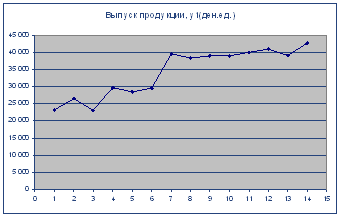
2. Для обнаружения тенденции в данном ВР воспользуемся критерием "восходящих и нисходящих" серий.

Критерий "восходящих и нисходящих" серий

1) Для исследуемого ВР определяется последовательность знаков, исходя из условий: (+), если , (-), если .

При этом, если последующее наблюдение равно предыдущему, то учитывается только одно наблюдение.

2) Подсчитывается число серий . Под серией понимается последовательность подряд расположенных плюсов или минусов, причем один плюс или один минус считается серией.

3) Определяется протяженность самой длинной серии .

4) Значение находят из следующей таблицы:

Таблица №25

Длина ряда,
Значение	5	6	7

5) Если нарушается хотя бы одно из следующих неравенств, то гипотеза об отсутствии тренда отвергается с доверительной вероятностью 0,95

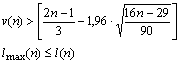
Определим последовательность знаков:

Таблица №19

t	Выпуск продукции, yt млн.долл.
1	23 298
2	26 570	+
3	23 080	-
4	29 800	+
5	28 440	-
6	29 658	+
7	39 573	+
8	38 435	-
9	39 002	+
10	39 020	+
11	40 012	+
12	41 005	+
13	39 080	-
14	42 680	+

Определим число серий : . Определим протяженность самой длинной серии : . , так как . Проверим выполнение неравенств:

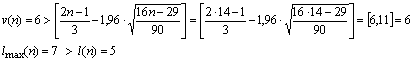
Вывод: второе неравенство не выполняются, следовательно, тренд (тенденция) в динамике выпуска продукции имеется на уровне значимости 0,05. Среднее значение . Среднее значение . Вычислим коэффициенты автокорреляции первого и второго порядков, то есть для лагов . Подготовим данные для вычисления коэффициентов автокорреляции первого и второго порядков. Дополним таблицу данных двумя столбцами .

Таблица №20

t	Yt	Yt-1	Yt-2
1	23 298
2	26 570	23 298
3	23 080	26 570	23 298
4	29 800	23 080	26 570
5	28 440	29 800	23 080
6	29 658	28 440	29 800
7	39 573	29 658	28 440
8	38 435	39 573	29 658
9	39 002	38 435	39 573
10	39 020	39 002	38 435
11	40 012	39 020	39 002
12	41 005	40 012	39 020
13	39 080	41 005	40 012
14	42 680	39 080	41 005

Вывод:

1) высокое значение коэффициента автокорреляции первого порядка свидетельствует об очень тесной зависимости между выпуском продукции текущего и непосредственно предшествующего годов, и, следовательно, о наличии в исследуемом временном ряде сильной линейной тенденции;

2) исследуемый ряд содержит только тенденцию, так как наиболее высоким оказался коэффициент автокорреляции первого порядка (0,85>0,83).

Скользящие средние найдем по формуле: , здесь . При

Вычисляем:

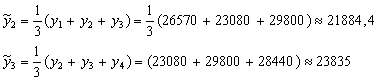
и так далее.

Результаты вычислений занесем в таблицу и построим графики исходногои сглаженного рядов в одной координатной плоскости.

Таблица №21

t	yi	yt
1	23 298
2	26 570	24 315,76
3	23 080	26 483,07
4	29 800	27 106,40
5	28 440	29 299,04
6	29 658	32 556,67
7	39 573	35 888,31
8	38 435	39 002,94
9	39 002	38 818,61
10	39 020	39 344,27
11	40 012	40 011,93
12	41 005	40 031,93
13	39 080	40 921,26
14	42 680

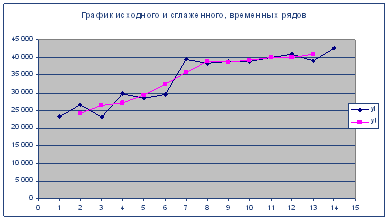
Таблица № Параметры (коэффициенты) уравнения тренда.

Таблица №22

	Коэффициенты
Y-пересечение	22686,54945
t	1543,250549

Анализ данных таблицы Дисперсионного анализа показывает, что получено статистически значимое уравнение, так как наблюдаемое значение , равное 52,785, превышает его табличное значение , . Вывод: Таким образом, параметры уравнения тренда статистически значимы на уровне : уравнение тренда можно использовать для прогноза.

Сделаем точечный и интервальный (с надежностью 0,95) прогнозы среднего и индивидуального значений прогнозов на 2003 год.

Определим точечный прогноз

Вычислим интервальный прогноз:

Так как тренд является прямой, то доверительный интервал можно представить в виде: .

Здесь стандартная ошибка предсказания по линии тренда вычисляется по формуле:

здесь величина является стандартной ошибкой регрессии, и ее значение находится в таблице Регрессионная статистика

Таблица №23

Стандартная ошибка

1637,180026

кратность ошибки (надежность) находят по таблице значений критерия Стьюдента; уровень значимости; число степеней свободы.

Итак, по условию задачи имеем:

Для вычисления стандартной ошибки предсказания по линии тренда необходимо вычислить и сумму .

Таблица № 24

t	yt	(t1-tcr) ^2
1	23 298	42,25
2	26 570	30,25
3	23 080	20,25
4	29 800	12,25
5	28 440	6,25
6	29 658	2,25
7	39 573	0,25
8	38 435	0,25
9	39 002	2,25
10	39 020	6,25
11	40 012	12,25
12	41 005	20,25
13	39 080	30,25
14	42 680	42,25
7,5	Сумма	227,5

Вычисляем 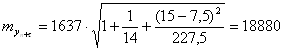(млн. долл.)

По таблице значений критерия Стьюдента найдем

Максимальная ошибка прогноза будет равна:

(млн. долл.).

Нижняя граница прогноза имеет значение (млн. долл.)

Верхняя граница прогноза имеет значение (млн. долл.)

Вывод:

1) значение выпуска продукции Финляндии в 2003 составит 20111,2 млн. долл.

2) с надежностью 0,95 данное значение будет находиться в интервале