
Рефераты по рекламе
Рефераты по физике
Рефераты по философии
Рефераты по финансам
Рефераты по химии
Рефераты по хозяйственному праву
Рефераты по экологическому праву
Рефераты по экономико-математическому моделированию
Рефераты по экономической географии
Рефераты по экономической теории
Рефераты по этике
Рефераты по юриспруденции
Рефераты по языковедению
Рефераты по юридическим наукам
Рефераты по истории
Рефераты по компьютерным наукам
Рефераты по медицинским наукам
Рефераты по финансовым наукам
Рефераты по управленческим наукам
Психология педагогика
Промышленность производство
Биология и химия
Языкознание филология
Издательское дело и полиграфия
Рефераты по краеведению и этнографии
Рефераты по религии и мифологии
Рефераты по медицине
Контрольная работа: Коэффициент детерминации. Значимость уравнения регрессии
Контрольная работа: Коэффициент детерминации. Значимость уравнения регрессии
Федеральное агентство по образованию
Всероссийский заочный финансово-экономический институт
Кафедра экономико-математических методов и моделей
КОНТРОЛЬНАЯ РАБОТА
по дисциплине «Эконометрика»
Вариант № 3
Исполнитель: Глушакова Т.И.
Специальность: Финансы и кредит
Курс: 3
Группа: 6
№ зачетной книжки: 07ффд41853
Руководитель: Денисов В.П.
г. Омск 2009г.
Задачи
По предприятиям легкой промышленности региона получена информация, характеризующая зависимость объема выпуска продукции (Y, млн. руб.) от объема капиталовложений (X, млн. руб.). Требуется:
1. Найти параметры уравнения линейной регрессии, дать экономическую интерпретацию коэффициента регрессии.
![]() - уравнение линейной регрессии,
где
- уравнение линейной регрессии,
где ![]() -
параметры уравнения.
-
параметры уравнения.
![]() , где
, где ![]() ,
,![]() - средние значения признаков.
- средние значения признаков.
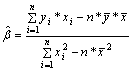 , где n – число наблюдений.
, где n – число наблюдений.
Представим вычисления в таблице 1:
Таблица 1. Промежуточные расчеты.
| t | xi | yi | yi * xi | xi*xi |
| 1 | 38 | 69 | 2622 | 1444 |
| 2 | 28 | 52 | 1456 | 784 |
| 3 | 27 | 46 | 1242 | 729 |
| 4 | 37 | 63 | 2331 | 1369 |
| 5 | 46 | 73 | 3358 | 2116 |
| 6 | 27 | 48 | 1296 | 729 |
| 7 | 41 | 67 | 2747 | 1681 |
| 8 | 39 | 62 | 2418 | 1521 |
| 9 | 28 | 47 | 1316 | 784 |
| 10 | 44 | 67 | 2948 | 1936 |
| средн. знач. | 35,5 | 59,4 | ||
|
|
2108,7 | |||
|
|
1260,25 | |||
|
|
21734 | |||
|
|
13093 | |||
| n | 10 | |||
|
|
1,319 | |||
|
|
12,573 |
Таким образом, уравнение линейной регрессии имеет вид:
![]()
Коэффициент регрессии равен 1,319>0, значит связь между объемом капиталовложений и выпуском продукции прямая, увеличение объема капиталовложений на 1 млн. руб. ведет к увеличению объема выпуска продукции в среднем на 1,319 млн. руб. Это свидетельствует об эффективности работы предприятий.
2. Вычислить остатки;
найти остаточную сумму квадратов; оценить дисперсию остатков ![]() ; построить график
остатков.
; построить график
остатков.
Вычислим прогнозное значение Y по формуле:
![]()
Остатки вычисляются по формуле:
![]() .
.
Представим промежуточные вычисления в таблице 2.
Таблица 2. Вычисление остатков.
|
|
|
|
|
| 69 | 62,695 | 6,305 | 39,75303 |
| 52 | 49,505 | 2,495 | 6,225025 |
| 46 | 48,186 | -2,186 | 4,778596 |
| 63 | 61,376 | 1,624 | 2,637376 |
| 73 | 73,247 | -0,247 | 0,061009 |
| 48 | 48,186 | -0,186 | 0,034596 |
| 67 | 66,652 | 0,348 | 0,121104 |
| 62 | 64,014 | -2,014 | 4,056196 |
| 47 | 49,505 | -2,505 | 6,275025 |
| 67 | 70,609 | -3,609 | 13,02488 |
Дисперсия остатков вычисляется по формуле:
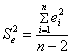
![]()
![]()
![]() .
.
Построим график остатков с помощью MS Excel.
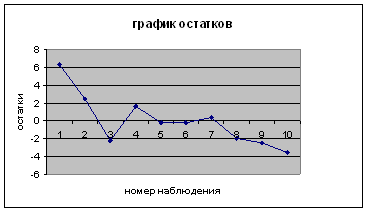
Рис. 1. График остатков.
3. Проверить выполнение предпосылок МНК
Проверим независимость остатков с помощью критерия Дарбина-Уотсона.
Вычислим коэффициент Дарбина-Уотсона по формуле:
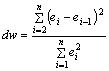 .
.
Данные для расчета возьмем из таблицы 2.
dw = 0,803
Сравним полученное
значение коэффициента Дарбина-Уотсона с табличными значениями границ ![]() и
и ![]() для уровня
значимости 0,05 при k=1 и n=10.
для уровня
значимости 0,05 при k=1 и n=10. ![]() =0,88,
=0,88, ![]() =1,32, dw < d
=1,32, dw < d![]() , значит, остатки содержат автокорреляцию. Наличие
автокорреляции нарушает одну из предпосылок нормальной линейной модели
регрессии.
, значит, остатки содержат автокорреляцию. Наличие
автокорреляции нарушает одну из предпосылок нормальной линейной модели
регрессии.
Проверим наличие гетероскедастичности. Т.к. у нас малый объем выборки (n=10) используем метод Голдфельда-Квандта.
- упорядочим значения n наблюдений по мере возрастания переменной x и разделим на две группы с малыми и большими значениями фактора x соответственно.
- рассчитаем остаточную сумму квадратов для каждой группы.
Вычисления представим в таблицах 3 и 4.
Таблица 3. Промежуточные вычисления для 1-го уравнения регрессии.
| t | xi | yi | yi * xi | xi*xi |
|
|
|
| 1 | 27 | 46 | 1242 | 729 | 47 | -1 | 1 |
| 2 | 27 | 48 | 1296 | 729 | 47 | 1 | 1 |
| 3 | 28 | 47 | 1316 | 784 | 49,5 | -2,5 | 6,25 |
| 4 | 28 | 52 | 1456 | 784 | 49,5 | 2,5 | 6,25 |
| средн. знач. | 27,5 | 48,25 | |||||
|
|
1326,875 | ||||||
|
|
756,25 | ||||||
|
|
5310,00 | ||||||
|
|
3026,00 | ||||||
| n | 4 | ||||||
|
|
2,5 | ||||||
|
|
- 20,5 | ||||||
|
|
14,5 |
Таблица 4. Промежуточные вычисления для 2-го уравнения регрессии.
| t | xi | yi | yi * xi | xi*xi |
|
|
|
| 1 | 37 | 63 | 2331 | 1369 | 63,789 | -0,789 | 0,623 |
| 2 | 38 | 69 | 2622 | 1444 | 64,582 | 4,418 | 19,519 |
| 3 | 39 | 62 | 2418 | 1521 | 65,375 | -3,375 | 11,391 |
| 4 | 41 | 67 | 2747 | 1681 | 66,961 | 0,039 | 0,002 |
| 5 | 44 | 67 | 2948 | 1936 | 69,340 | -2,340 | 5,476 |
| 6 | 46 | 73 | 3358 | 2116 | 70,926 | 2,074 | 4,301 |
| средн. знач. | 40,833 | 66,833 | |||||
|
|
2729,028 | ||||||
|
|
1667,361 | ||||||
|
|
16424 | ||||||
|
|
10067 | ||||||
| n | 6 | ||||||
|
|
0,793 | ||||||
|
|
34,448 | ||||||
|
|
41,310 |
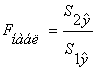 =
= ![]() =
=![]() 2,849
2,849
где ![]() - остаточная сумма
квадратов 1-ой регрессии,
- остаточная сумма
квадратов 1-ой регрессии, ![]() - остаточная сумма квадратов 2-ой
регрессии.
- остаточная сумма квадратов 2-ой
регрессии.
Полученное значение
сравним с табличным значением F
распределения для уровня значимости ![]() , со степенями свободы
, со степенями свободы ![]() и
и ![]() (
(![]() - число
наблюдений в первой группе, m –
число оцениваемых параметров в уравнении регрессии).
- число
наблюдений в первой группе, m –
число оцениваемых параметров в уравнении регрессии).
![]() ,
, ![]() , m=1.
, m=1.
Если 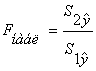 >
> ![]() , то имеет место
гетероскедастичность.
, то имеет место
гетероскедастичность.
![]() = 5,41
= 5,41
![]() <
< ![]() ,
,
значит, гетероскедастичность отсутствует и предпосылка о том, что дисперсия остаточных величин постоянна для всех наблюдений выполняется.
4. Осуществить проверку
значимости параметров уравнения регрессии с помощью t-критерия Стьюдента ![]() .
.
Расчетные значения t-критерия можно вычислить по формулам:
![]() ,
, 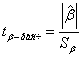
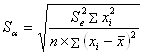 ,
, 
![]() ,
,
![]()
![]()
![]()
![]() =35,5
=35,5
Промежуточные расчеты представим в таблице:
Таблица 5. Промежуточные вычисления для расчета t- критерия
| xi |
|
| 38 | 6,25 |
| 28 | 56,25 |
| 27 | 72,25 |
| 37 | 2,25 |
| 46 | 110,25 |
| 27 | 72,25 |
| 41 | 30,25 |
| 39 | 12,25 |
| 28 | 56,25 |
| 44 | 72,25 |
![]() =490,50
=490,50
![]()
![]()
![]()
![]()
![]() для уровня значимости 0,05 и
числа степеней свободы n-2=8
для уровня значимости 0,05 и
числа степеней свободы n-2=8
Так как ![]() и
и ![]() можно сделать вывод,
что оба коэффициента регрессии значимые.
можно сделать вывод,
что оба коэффициента регрессии значимые.
5. Вычислить коэффициент
детерминации, проверить значимость уравнения регрессии с помощью F-критерия Фишера ![]() , найти среднюю
относительную ошибку аппроксимации. Сделать вывод о качестве модели.
, найти среднюю
относительную ошибку аппроксимации. Сделать вывод о качестве модели.
Коэффициент детерминации определяется по формуле:
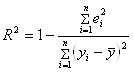
Из расчетов нам известно, что
![]() ;
; ![]() .
.
Рассчитаем ![]() :
:
Таблица 6. Промежуточные вычисления для расчета коэффициента детерминации.
|
|
|
|
| 69 | 9,6 | 92,16 |
| 52 | -7,4 | 54,76 |
| 46 | -13,4 | 179,56 |
| 63 | 3,6 | 12,96 |
| 73 | 13,6 | 184,96 |
| 48 | -11,4 | 129,96 |
| 67 | 7,6 | 57,76 |
| 62 | 2,6 | 6,76 |
| 47 | -12,4 | 153,76 |
| 67 | 7,6 | 57,76 |
![]()
![]() =930,4
=930,4
![]() =0,917.
=0,917.
Т.к. значение коэффициента детерминации близко к единице, качество модели считается высоким.
Теперь проверим
значимость уравнения регрессии. Рассчитаем значение F-критерия Фишера ![]() по формуле:
по формуле:
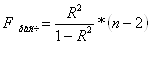
![]()
![]()
Уравнение регрессии с
вероятностью 0,95 в целом статистически значимое, т.к. ![]() >
>![]() .
.
Средняя относительная ошибка аппроксимации находится по формуле:
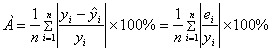
Таблица 7. Промежуточные вычисления для расчета средней относительной ошибки аппроксимации.
| yi |
|
|
| 69 | 6,305 | 0,091377 |
| 52 | 2,495 | 0,047981 |
| 46 | -2,186 | 0,047522 |
| 63 | 1,624 | 0,025778 |
| 73 | -0,247 | 0,003384 |
| 48 | -0,186 | 0,003875 |
| 67 | 0,348 | 0,005194 |
| 62 | -2,014 | 0,032484 |
| 47 | -2,505 | 0,053298 |
| 67 | -3,609 | 0,053866 |
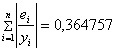
![]() ,
,
значит модель имеет хорошее качество.
Рассчитаем коэффициент эластичности по формуле:
![]()
![]()
6. осуществить
прогнозирование среднего значения показателя Y при уровне значимости ![]() , если прогнозное значение фактора
X составит 80% от его максимального
значения.
, если прогнозное значение фактора
X составит 80% от его максимального
значения.
![]()
Рассчитаем стандартную ошибку прогноза
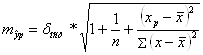 ,
,
где![]()
![]() =930,4 ;
=930,4 ; ![]()
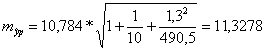
![]()
![]() ,
, ![]() для уровня значимости 0,1 и числа
степеней свободы n-2=8
для уровня значимости 0,1 и числа
степеней свободы n-2=8
![]()
Доверительный интервал прогноза:
![]()
![]()
Таким образом, ![]() =61,112 , будет
находиться между верхней границей, равной 82,176 и нижней границей, равной 40,048.
=61,112 , будет
находиться между верхней границей, равной 82,176 и нижней границей, равной 40,048.
7. Представить графически фактические и модельные значения Y точки прогноза.
Воспользуемся данными из таблицы 2 для построения графиков с помощью MS Excel.
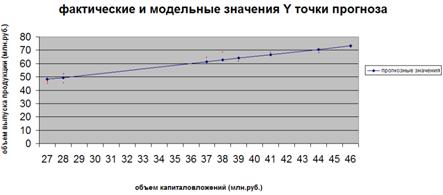
Рис. 2. Фактические и модельные значения Y точки прогноза.
8. Составить уравнения нелинейной регрессии: гиперболической, степенной, показательной. Привести графики построенных уравнений регрессии.
Построение степенной модели.
Уравнение степенной модели имеет вид:
![]()
Для построения этой модели необходимо произвести линеаризацию переменных. Для этого произведем логарифмирование обеих частей уравнения:
![]()
Обозначим ![]() .
.
Тогда уравнение примет
вид ![]() –
линейное уравнение регрессии. Рассчитаем его параметры, используя данные
таблицы 1:
–
линейное уравнение регрессии. Рассчитаем его параметры, используя данные
таблицы 1:
Таблица 8. Расчет параметров уравнения степенной модели регрессии.
| t | xi | X |
|
Y | YX | X*X |
|
|
|
|
| 1 | 38 | 1,5798 | 69 | 1,839 | 2,905 | 2,496 | 62,347 | 6,653 | 9,642 | 44,26 |
| 2 | 28 | 1,447 | 52 | 1,716 | 2,483 | 2,094 | 50,478 | 1,522 | 2,926 | 2,315 |
| 3 | 27 | 1,431 | 46 | 1,663 | 2,379 | 2,048 | 49,225 | -3,225 | 7,010 | 10,399 |
| 4 | 37 | 1,568 | 63 | 1,799 | 2,821 | 2,459 | 61,208 | 1,792 | 2,845 | 3,212 |
| 5 | 46 | 1,663 | 73 | 1,863 | 3,098 | 2,765 | 71,153 | 1,847 | 2,530 | 3,411 |
| 6 | 27 | 1,431 | 48 | 1,681 | 2,406 | 2,049 | 49,225 | -1,225 | 2,552 | 1,5 |
| 7 | 41 | 1,613 | 67 | 1,826 | 2,945 | 2,601 | 65,771 | 1,289 | 1,924 | 1,66 |
| 8 | 39 | 1,591 | 62 | 1,793 | 2,853 | 2,531 | 63,477 | -1,477 | 2,382 | 2,182 |
| 9 | 28 | 1,447 | 47 | 1,672 | 2,419 | 2,094 | 50,478 | -3,478 | 7,4 | 12,099 |
| 10 | 44 | 1,644 | 67 | 1,826 | 3,001 | 2,701 | 68,999 | -1,999 | 2,984 | 3,997 |
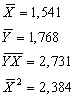
![]()
![]()
Уравнение регрессии будет иметь вид:
![]()
Перейдем к исходным переменным x и y, выполнив потенцирование данного уравнения:
![]()
![]()
Вычислим коэффициент
детерминации ![]() :
:
![]() =930,4;
=930,4; ![]()
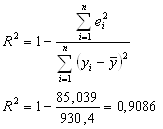 (1)
(1)
Вычислим среднюю ошибку аппроксимации А:
![]() %
%
 (2)
(2)
Коэффициент эластичности рассчитывается по формуле:
![]() (3)
(3)
![]()
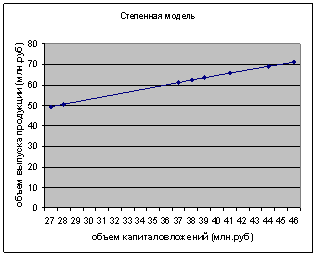
Рис. 3. График степенного уравнения регрессии.
Построение показательной функции.
Уравнение показательной
кривой:![]()
Для построения этой модели необходимо произвести линеаризацию переменных. Для этого осуществим логарифмирование обеих частей уравнения:
![]()
Обозначим ![]()
Получим линейное уравнение регрессии:
![]()
Рассчитаем его параметры, используя данные таблиц 1 и 8.
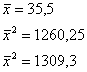
Промежуточные расчеты представим в таблице 9.
Таблица 9. Промежуточные расчеты для показательной функции.
| t | xi | Y |
|
y |
|
|
|
|
| 1 | 38 | 1,839 | 69,882 | 69 | 62,632 | 6,368 | 10,167 | 40,552 |
| 2 | 28 | 1,716 | 48,048 | 52 | 49,893 | 2,107 | 4,223 | 4,44 |
| 3 | 27 | 1,663 | 44,901 | 46 | 48,771 | -2,771 | 5,682 | 7,68 |
| 4 | 37 | 1,799 | 66,563 | 63 | 61,224 | 1,776 | 2,901 | 3,155 |
| 5 | 46 | 1,863 | 85,698 | 73 | 75,128 | -2,128 | 2,832 | 4,528 |
| 6 | 27 | 1,681 | 45,387 | 48 | 48,771 | -0,771 | 1,581 | 0,595 |
| 7 | 41 | 1,826 | 74,866 | 67 | 67,054 | -0,054 | 0,08 | 0,003 |
| 8 | 39 | 1,793 | 69,927 | 62 | 64,072 | -2,072 | 3,235 | 4,295 |
| 9 | 28 | 1,672 | 46,816 | 47 | 49,893 | -2,893 | 5,798 | 8,369 |
| 10 | 44 | 1,826 | 80,344 | 67 | 71,788 | -4,788 | 6,669 | 22,921 |
![]() =63,2432
=63,2432
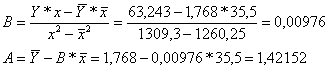
Уравнение будет иметь вид:
![]()
Перейдем к исходным переменным x и y, выполнив потенцирование данного уравнения:
![]()
Рассчитаем коэффициент детерминации по формуле (1).
![]() =930,4;
=930,4; ![]()
![]()
Вычислим среднюю ошибку аппроксимации А по формуле (2):
![]()
А=0,1*43,170=4,317%
Коэффициент эластичности рассчитаем по формуле (3):
![]() %
%
Построим график функции с помощью MS Excel.
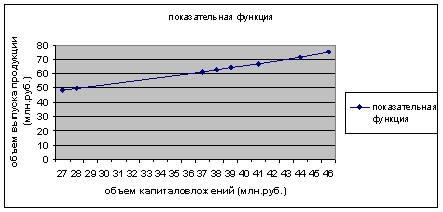
Рис. 4. График показательного уравнения регрессии.
Построение гиперболической функции.
Уравнение гиперболической
функции ![]()
Произведем линеаризацию модели путем замены Х=1/х.
В результате получим
линейное уравнение: ![]()
Рассчитаем параметры уравнения, промежуточные вычисления представим в таблице 10.
Таблица 10. Расчет параметров для гиперболической модели.
| t | xi | yi | X=1/xi | y*X |
|
|
|
|
|
| 1 | 38 | 69 | 0,02632 | 1,81579 | 0,00069 | 63,5648 | 5,4352 | 7,877 | 29,5409 |
| 2 | 28 | 52 | 0,03571 | 1,85714 | 0,00128 | 50,578 | 1,422 | 2,7346 | 2,0221 |
| 3 | 27 | 46 | 0,03704 | 1,7037 | 0,00137 | 48,7502 | -2,7502 | 5,9787 | 7,5637 |
| 4 | 37 | 63 | 0,02703 | 1,7027 | 0,00073 | 62,5821 | 0,4179 | 0,6634 | 0,1747 |
| 5 | 46 | 73 | 0,02174 | 1,58696 | 0,00047 | 69,8889 | 3,1111 | 4,2618 | 9,6791 |
| 6 | 27 | 48 | 0,03704 | 1,77778 | 0,00137 | 48,7502 | -0,7502 | 1,563 | 0,5628 |
| 7 | 41 | 67 | 0,02439 | 1,63415 | 0,00059 | 66,2256 | 0,7744 | 1,1559 | 0,5998 |
| 8 | 39 | 62 | 0,02564 | 1,58974 | 0,00066 | 64,4972 | -2,4972 | 4,0278 | 6,2362 |
| 9 | 28 | 47 | 0,03571 | 1,67857 | 0,00128 | 50,578 | -3,578 | 7,6128 | 12,8021 |
| 10 | 44 | 67 | 0,02273 | 1,52273 | 0,00052 | 68,5235 | -1,5235 | 2,2738 | 2,3209 |

![]()
![]()
![]()
![]()
Уравнение гиперболической модели:
![]()
Рассчитаем коэффициент детерминации по формуле (1).
![]() =930,4;
=930,4; ![]()
![]()
Вычислим среднюю ошибку аппроксимации А по формуле (2):
![]()
А=0,1*38,1488=3,81488%
Коэффициент эластичности рассчитаем по формуле (3):
![]()
![]() %
%
Построим график функции с помощью MS Excel.
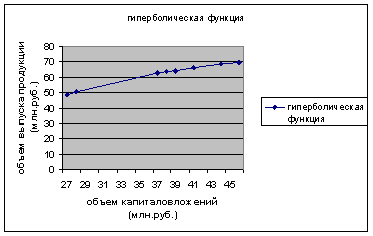
Рис. 5 График гиперболического уравнения регрессии.
9. Для указанных моделей найти коэффициенты детерминации, коэффициенты эластичности и средние относительные ошибки аппроксимации. Сравнить модели по этим характеристикам и сделать выводы.
Коэффициенты были рассчитаны в задании 8. Для сравнения моделей составим сводную таблицу 11:
Таблица11. Сводная таблица характеристик моделей.
|
параметры модель |
Коэффициент детерминации, R |
Коэффициент эластичности, |
Средняя относительная ошибка аппроксимации, А (%) |
| Линейная | 0,917 | 0,788 | 3,648 |
| Степенная | 0,909 | 0,692 | 4,22 |
| Показательная | 0,896 | 0,817 | 4,317 |
| Гиперболическая | 0,923 | 0,638 | 3,815 |
Для всех моделей средняя
относительная ошибка аппроксимации не превышает 7%, значит, качество всех
моделей хорошее. Коэффициент детерминации более приближен к 1 у гиперболической
модели, таким образом, эту модель можно взять в качестве лучшей для построения
прогноза. Для гиперболической модели степень связи между факторным и
результативным признаком самая низкая, т.к. ![]() имеет наименьшее значение, а для
показательной модели самая высокая, т.к. коэффициент эластичности наибольший.
имеет наименьшее значение, а для
показательной модели самая высокая, т.к. коэффициент эластичности наибольший.