Контрольная работа: Экономическая интерпретация коэффициента регрессии

Министерство образования и науки РФ

Федеральное агентство по образованию ГОУ ВПО

Всероссийский заочный финансово-экономический институт

КОНТРОЛЬНАЯ РАБОТА

по Эконометрике

вариант № 6

К.ф. – м.н., доцент кафедры: Василенко В.В.

Студент: Чмиль А.А., ФиК, 3 Курс

Краснодар, 2009

По предприятиям легкой промышленности региона получена информация, характеризующая зависимость объема выпуска продукции (Y, млн.руб.) от объема капиталовложений (X, млн.руб.).

Xi	Yi
33	43
17	27
23	32
17	29
36	45
25	35
39	47
20	32
13	22
12	24

Исходные данные.Табл.1

n	Xi	Yi	Yi*Xi	Xi2	Yi2	Y(xi)	Yi - Y(xi)	(Yi - Y(xi))2	A
1	33	43	1419	1089	1849	42,23428	0,765721183	0,5863289	1,78%
2	17	27	459	289	729	27,69234	-0,692335546	0,4793285	2,56%
3	23	32	736	529	1024	33,14556	-1,145564273	1,3123175	3,58%
4	17	29	493	289	841	27,69234	1,307664454	1,7099863	4,51%
5	36	45	1620	1296	2025	44,96089	0,03910682	0,0015293	0,09%
6	25	35	875	625	1225	34,96331	0,036692818	0,0013464	0,10%
7	39	47	1833	1521	2209	47,68751	-0,687507544	0,4726666	1,46%
8	20	32	640	400	1024	30,41895	1,581050091	2,4997194	4,94%
9	13	22	286	169	484	24,05685	-2,056849728	4,2306308	9,35%
10	12	24	288	144	576	23,14798	0,852021726	0,725941	3,55%
сумма	235	336	8649	6351	11986	336	0,00	12,019795	31,93%
средняя	23,5	33,6	864,9	635,1	1198,6	33,6	0,00	1,2019795	3,19%
δ	9,102198	8,345058	-	-	-	-	-	-	-
δ2	82,85	69,64	-	-	-	-	-	-	-

Вспомогательная таблица для расчетов параметров линейной регрессии. Табл.2

Задание 1

Найти параметры уравнения линейной регрессии, дать экономическую интерпретацию коэффициента регрессии.

После проведенных расчетов линейная модель имеет вид:

Y = 12,24152 + 0,908871x , коэффициент регрессии составил 0,908871. Экономический смысл параметра регрессии заключается в следующем: с увеличением капиталовложений на 1 единицу выпуск продукции увеличивается на 0,908871 единиц.

Задание 2

Вычислить остатки; найти остаточную сумму квадратов; оценить дисперсию остатков; построить график остатков.

Вычисленные остатки приведены в таблице 2. Остаточная сумма квадратов составила 12,02. Дисперсия остатков составила:

Dост = ((Y- Yср.)2 - (Y(xi) - Yср.)2)/ (n – 2) = 1,502474351.

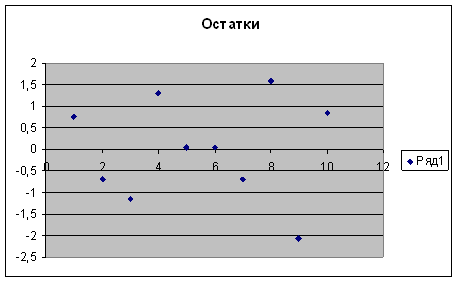
График остатков. Рис.1

Задание 3

Проверить выполнение предпосылок МНК.

Остатки гомоскедастичны, автокорреляция отсутствует (корреляция остатков и фактора Х равна нулю, рис.1), математическое ожидание остатков равно нулю, остатки нормально распределены.

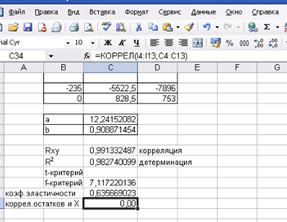
Корреляция остатков и переменной Х. Рис 2.

Задание 4

Осуществить проверку значимости параметров уравнения регрессии с помощью t – критерия Стьюдента (α = 0,05).

Найдем стандартную ошибку коэффициента регрессии:

mb = (Dост. / ∑(x – xср.) 2 ) ½ = 0,042585061

Теперь проведем оценку значимости коэффициента регрессии:

tb = b / mb = 21,3424949

При α = 0,05 и числе степеней свободы (n – 2) tтабл. = 2,3060. Так как фактическое значение t – критерия больше табличного, то гипотезу о несущественности коэффициента можно отклонить. Доверительный интервал для коэффицента регрессии определяется как b ± t* mb. Для коэффициента регрессии b границы составят: 0,908871 – 2,3060*0,042585061 ≤ b ≤ 0,908871+2,3060*0,042585061

0,81067 ≤ b ≤ 1,0070722

Далее определим стандартную ошибку параметра a:

ma = (Dост.*( ∑x2 / (n*∑(x – xср.)2 ))1/2 = 1,073194241

ta = a / ma = 11,4066218

Мы видим, что фактическое значение параметра а больше, чем табличное, следовательно, гипотезу о несущественности параметра а можно отклонить. Доверительный интервал составит: a ± t* ma. Границы параметра составят:

12,24152 ± 2,3060*1,073194241

9,766735 ≤ a ≤ 14,716305

Проверим значимость линейного коэффициента корреляции на основе ошибки коэффициента корреляции:

mr = ((1 – r2) / (n – 2))1/2 = 0,046448763

Фактическое значение t – критерия Стьюдента определяется:

tr = (r / (1 – r2)) * (n – 2)1/2 = 21,3424949

Значение tr фактическое больше табличного, следовательно при уровне значимости α = 0,05 и степени свободы (n – 2), коэффициент корреляции существенно отличен от нуля и зависимость является достоверной.

Задание 5

Вычислить коэффициент детерминации, проверить значимость уравнения регрессии с помощью f – критерия Фишера (α = 0,05), найти среднюю относительную ошибку аппроксимации. Сделать вывод о качестве модели.

R2 = Rxy2 = 0,98274 – детерминация.

F = (R2/(1 – R2))*((n – m – 1)/m) = 455,5020887

Fтабл. 5,32 < Fкр. 455,5020887– это говорит о том, что уравнение регрессии статистически значимо.

Средняя ошибка аппроксимации А = 3,19%. Это говорит о том, что качество уравнения регрессии хорошее. Расчетные значения отклоняются от фактических на 3,19%.

Задание 6

Осуществить прогнозирование среднего значения показателя Y при уровне значимости α = 0,1, если прогнозное значение фактора X составит 80% от максимального значения.

Если прогнозируемое значение Хр = 0,8Хmax = 0,8*39 = 31,2 млн.руб., тогда прогнозное значение объема капиталовложений составит:

Yр = 12,24152 + 0,908871*31,2 = 40,598295 млн.руб.

Ошибка прогноза составит:

myр = Dост.*(1+(1/n)+((xk – xср)2 / ∑(x – xср)2 )1/2 = 1,502474351*(1+(1/10)+ ((31,2 – 23,5)2 / 828,50))1/2 = 1,6262596 млн.руб.

Предельная ошибка прогноза, которая в 90% случаев не будет превышена, составит:

Δyp = tтабл * myр = 2,3060 * 1,6262596 = 3,7501546

Доверительный интервал прогноза:

γур = Yр ± Δyp

γурmin = 40,598295 – 3,7501546 = 36,848141 млн.руб.

γурmax = 40,598295 + 3,7501546 = 44,348449 млн.руб.

Среднее значение показателя составит:

Yp = (36,848141 + 44,348449) / 2 = 40,598295 млн.руб.

Задание 7

Представить графически фактические и модельные значения Y точки прогноза

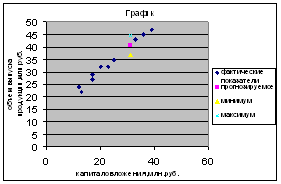
График фактических и прогнозируемых параметров. Рис.3

Задание 8

Составить уравнения нелинейной регрессии:

· Гиперболической

· Степенной

· Показательной

Построить графики построенных уравнений регрессии.

Y(x) = 54,1842 + (-415,755) * 1/x – гиперболическое уравнение регрессии.

Y(x) = 4,746556 * X0,625215 – степенное уравнение регрессии.

Y(x) = 17,38287 * 1,027093X показательное уравнение регрессии.

Графики моделей представлены ниже на рисунках 4,5 и 6.

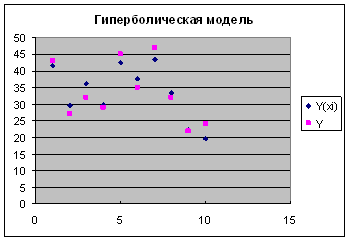
Рис.4

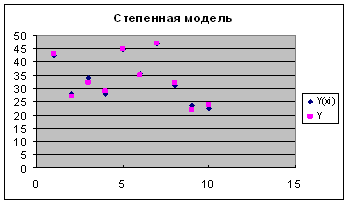
Рис.5

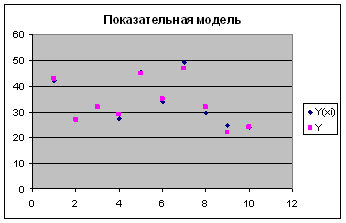
Рис.6

Задание 9

Для указанных моделей найти коэффициенты детерминации, коэффициент эластичности и средние относительные ошибки аппроксимации. Сравнить модели по этим характеристикам и сделать выводы.

Коэффициенты (индексы) детерминации:

R2гип = Rxy = 0,869064776

R2степ = Rxy = 0,978207122

R2показ = Rxy = 0,959136358

Коэффициенты эластичности:

Эгип = -b / (a * x + b) = 0,484804473

Эстеп = b = 0,625215

Эпоказ = x * lnb = 0,628221

Средние относительные ошибки аппроксимации:

А = 1/n * ∑ |y – yxi| * 100%

Агип = 7,26%

Астеп = 3,40%

Апоказ = 3,82%

Как мы видим, степенная регрессия наиболее интересна в экономическом смысле, потому что у нее самый низкий показатель средней ошибки аппроксимации, самый высокий показатель эластичности и детерминации. Это говорит о том, что у степенной регрессионной модели высокое качество, она предлагает наибольшую прибыль и более зависима от фактора Х (капиталовложений).

Список использованной литературы

1. Практикум по эконометрике: Учеб. пособие / И.И. Елисеева, С.В. Курашева, Н.М. Гордеенко и др.; Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2001. – 192.: ил.

2. Эконометрика. Учебник для вузов.; Под ред. чл. – кор. РАН И.И. Елисеевой. – М.: Финансы и статистика, 2002. – 344.