Реферат: Конечные разности. Погрешности

Реферат: Конечные разности. Погрешности

Реферат

«Конечные разности. Погрешности»

1. Погрешности

1.1 Действительные и конечно-разрядные числа

Представление действительных чисел в вычислительных машинах с фиксированной разрядной сеткой влечет появление инструментальной погрешности в обрабатываемых числах и результатах арифметических действий.

Принятое при вводе преобразование исходных действительных чисел в нормализованную экспоненциальную форму и размещение их в ограниченной разрядной сетке ЭВМ с порядком и дробной частью (мантиссой) в общем случае вносит в этот операнд относительную инструментальную погрешность, величина которой не превышает

где n – число значащих дробных двоичных разрядов, отведенных для хранения мантиссы.

Приближенное конечно-разрядное число a – это действительное число, занимающее заданное количество разрядов и округленное до числа с ближайшим значением достоверного младшего разряда. Приближенные действительные числа имеют абсолютную  и относительную  погрешности. Эти погрешности при анализе распространения ошибки при вычислениях приписываются к приближенному числу результата и связываются между собой следующим образом:

Если число a = 5,3812 имеет все разряды достоверные, то его абсолютная погрешность принимается равной половине единицы младшего разряда, т.е. =0.00005, а относительная погрешность, округляемая обычно до одного-двух значащих достоверных разрядов, будет

Всякие арифметические операции с операндами, представленными в системе с плавающей точкой, в общем случае вносят в результат аналогичную относительную инструментальную погрешность:

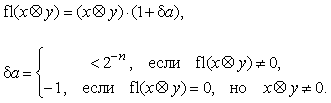
где fl(•) – указание на арифметику с плавающей точкой,

 – арифметическая операция из множества .

Значение результата, равное нулю принудительно устанавливается в машинах при операциях умножения с двумя операндами, приводящее к исчезновению порядка (отрицательный порядок по модулю не умещается на отведенном для него количестве разрядов).

Несколько иначе обстоит дело при вычитании чисел с плавающей точкой и одинаковым порядком:

,

.

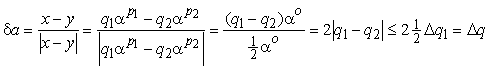Из последнего можно заключить, что для операции вычитания относительная погрешность численно определяется количеством значащих разрядов в результате, которое из-за выполнения нормализации не может быть меньше . Т.е. погрешность приближается к 100% последовательно. Это предупреждение адресуется составителям вычислительных алгоритмов, которым необходимо выискивать эквивалентные формулы с контролем величины операндов, в определенных ситуациях можно использовать программный переход к вычислениям с удвоенной точностью.

При выполнении аддитивных операций с приближенными операндами погрешность результата равна сумме абсолютных погрешностей всех чисел, участвовавших в операции. Выполнение мультипликативных операций вносит в результат относительную погрешность, равную сумме относительных погрешностей каждого из операндов.

1.2 Погрешность алгоритмов

Инструментальные погрешности арифметических машинных команд из-за различия и непредсказуемости величины ошибки результата нарушают дистрибутивный, ассоциативный и коммутативный законы арифметики. Каждый же программист, составляя программу, уже на уровне интуиции пользуется ими, как незыблемыми. Отсюда различие в точности тех или иных вычислительных алгоритмов и трудно уловимые ошибки.

Проследить накопление вычислительной погрешности алгоритма для операндов, которые имеют производные, удобно, если результат r каждой двуместной арифметической операции умножать на множитель  с последующим разложением результирующей функции алгоритма по степеням этого множителя или этих множителей, если  в группах операторов отличаются по величине. Например, для алгоритма вычисления значения полинома  третьей степени по схеме Горнера с псевдокодом:

P:=0; j:=3;

repeat

S:=a[j]*x+a [j-1];

P:=P+S*x;

j:=j-1;

until j=1;

функция алгоритма будет:

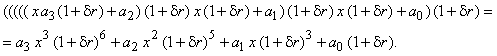
Учитывая, что , последнее выражение дает возможность после раскрытия скобок выделить из суммы и оценить сначала абсолютную погрешность, а по абсолютной погрешности – относительную:

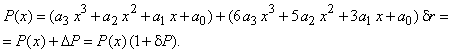
Условные арифметические операторы с проверкой равенства операндов необходимо заменять проверкой вида: .

2. Конечные разности

2.1 Определение конечных разностей

Конечная разность «вперед» для таблично заданной функции в i-той точке определяется выражением: , где функция  задана, как функция целочисленного аргумента с единичным шагом по аргументу i.

Для аналитически заданной и протабулированной с постоянным шагом h функции  определяющее соотношение имеет вид:

.

Преобразование таблицы функции  в функцию целочисленного аргумента  осуществляют при помощи линейного соотношения между аргументами x и i: .

Коэффициенты a и b находят из системы уравнений, получаемой в результате подстановки в пределах заданной таблицы вместо x и i сначала начальных значений аргументов , а затем конечных . При этом начало таблицы удобно совместить с началом координат функции с целочисленным аргументом(). Тогда для таблицы с (n+1) – й строками:

,

Повторные конечные разности n-го порядка в i-той точке для табличной функции  определяются соотношением

.

2.2 Конечно-разностные операторы

Линейность конечно-разностного оператора  позволяет ввести конечно-разностный оператор сдвига  и многочлены от оператора  с целыми коэффициентами, такие, как , где  должно рассматриваться как оператор повторной разности k-того порядка.

Действие любого многочлена  на функцию g(i) определяется как

.

Применение оператора сдвига к g(i) преобразует последнее в g (i+1):

g (i+1) = E g(i) = (1+) g(i)= g(i) + g(i).

Повторное применение оператора сдвига позволяет выразить (i+n) – е значение ординаты функции g через конечные разности различных порядков:

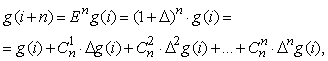
где  – число сочетаний из n элементов по k;

 – многочлен степени k от целой переменной n (), имеющий k сомножителей. При k=n .

В силу линейности оператора сдвига можно конечно-разностный оператор выразить, как , и определить повторные конечные разности через многочлены от операторов сдвига так .

Последнее позволяет формульно выражать n-ную повторную разность через (n+1) ординату табличной функции, начиная с i-той строки:

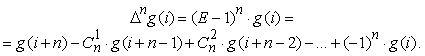
Если в выражении для g (i+n) положить i=0 и вместо  подставить их факториальные представления, то после несложных преобразований получится разложение функции целочисленного аргумента по многочленам , которые в литературе называют факториальными:

.

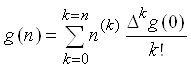Можно поставить задачу разложения и функции действительной переменной f(x) по многочленам  относительно начала координат (аналогично ряду Маклорена), т.е. . Если последовательно находить конечные разности от левой и правой частей, то, зная, что  и , после подстановки x=0 будем получать выражения для коэффициентов разложения . У многочленов k-той степени, , поэтому

.

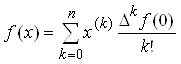Такое разложение табличной функции f(x) в литературе называют интерполяционным многочленом Ньютона для равных интервалов.

2.3 Взаимосвязь операторов разности и дифференцирования

Значение функции на удалении h от некоторой точки  можно выразить через значения производных в этой точке, разложив ее в ряд Тейлора:

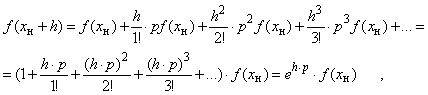
где  – оператор дифференцирования,

 – оператор сдвига, выраженный через оператор p.

h – шаг по оси действительной переменной

Из равенства операторов сдвига, выраженных через p и , можно получить взаимосвязь этих линейных операторов:

,

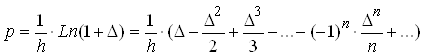Оператор дифференцирования порядка n, перенесенный в точку, удаленную от текущей, например, на 2 шага вперед представляется так:

.

Выполнив алгебраическое перемножение многочленов с конечно-разностными операторами и ограничившись операторами со степенью не выше n, получим одну из возможных аппроксимаций оператора дифференцирования. Действуя таким сложным конечно-разностным оператором на ординату f(x), получаем формулу для вычисления n-й производной в точке  по значениям ее конечных разностей. Например, для n=2, отбрасывая все повторные разности выше третьего порядка, получим:

.

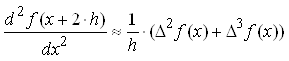Если f(x) является многочленом степени n, то повторные разности (n+1) – го порядка тождественно равны нулю. Приравнивая нулю повторные разности порядков выше n мы фактически аппроксимируем f(x) многочленом степени n.

В предыдущем выражении, выразив повторные разности через ординаты табличной функции, получим еще один вид формулы для вычисления значения производной:

.

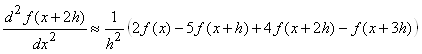Для целочисленного аргумента табличной функции запись выражения можно упростить, если положить h=1 и

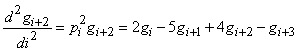
2.4 Исчисление конечных разностей

Разложение функций в ряд по факториальным многочленам (интерполяционным многочленам Ньютона в частности) дает возможность получать формулы суммирования функциональных рядов в виде аналитических выражений, зависящих от пределов. Эта возможность открывается в связи с тем, что суммировать конечные разности не представляет большой сложности, а выразить конечную разность от факториального многочлена через факториальный же многочлен можно, воспользовавшись соотношением:

Факториальные многочлены по отношению к исчислению разностей ведут себя так же, как степенные функции в исчислении производных: дифференцирование тоже понижает степень многочлена на единицу. Это свойство позволяет в факториальном разложении заменить факториальные многочлены своими конечными разностями следующего вида:

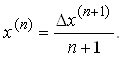
Замена хороша тем, что суммирование конечных разностей в заданных пределах мнемонически весьма напоминает вычисление определенного интеграла от функции по ее первообразной:

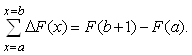
Если , то

.

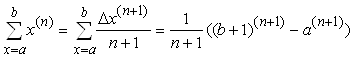Процедуру суммирования функционального ряда продемонстрируем на примере получения суммы квадратов натурального ряда чисел в пределах от a=1 до b=5 (Для проверки: ):

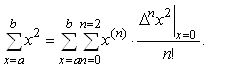
Вторая сумма по переменной n представляет разложение  по факториальным многочленам, в которое входят значения конечных разностей 0, 1 и 2-го порядков, вычисленные в начале координат целочисленной переменной, т.е. при x=0. Они соответственно равны:

,

,

.

После подстановки значений разностей во второй сумме останутся два факториальных полинома: первой и второй степеней:

Если распределить вычисление сумм по слагаемым, то мы перейдем к суммированию конечных разностей от факториальных многочленов:

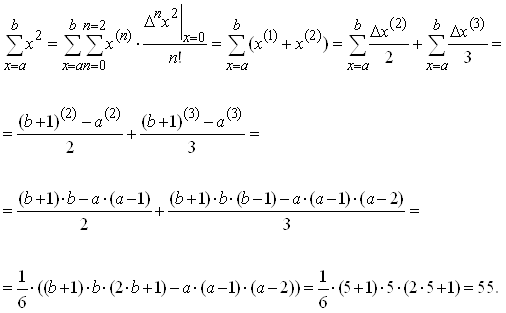
Литература

1.  Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы: Учеб. пособие. – М.: Наука, 1987. – 600 с.

2.  Воеводин В.В. Численные методы алгебры. Теория и алгорифмы. – М.: Наука, 1966. – 248 с.

3.  Воеводин В.В. Вычислительные основы линейной алгебры. – М.: Наука, 1977. – 304 с.

4.  Волков Е.А. Численные методы. – М.: Наука, 1987. – 248 с.

5.  Калашников В.И. Аналоговые и гибридные вычислительные устройства: Учеб. пособие. – Харьков: НТУ «ХПИ», 2002. – 196 с.

6.  Вержбицкий, В.М. Численные методы. Математический анализ и обыкновенные дифференциальные уравнения. М.: Высш.шк., 2001. 383 с.

7.  Волков, Е.А. Численные методы. СПб.: Лань, 2004. 248 с.

8.  Мудров, А.Е. Численные методы для ПЭВМ на языках Бейсик, Фортран и Паскаль. Томск: МП «РАСКО», 1991. 272 с.

9.  Шуп, Т.Е. Прикладные численные методы в физике и технике. М.: Высш. шк., 1990. 255 с.

10.  Бахвалов, Н.С. Численные методы в задачах и упражнениях / Н.С. Бахвалов, А.В. Лапин, Е.В. Чижонков. М.: Высш. шк., 2000. 192 с.