
Рефераты по рекламе
Рефераты по физике
Рефераты по философии
Рефераты по финансам
Рефераты по химии
Рефераты по хозяйственному праву
Рефераты по экологическому праву
Рефераты по экономико-математическому моделированию
Рефераты по экономической географии
Рефераты по экономической теории
Рефераты по этике
Рефераты по юриспруденции
Рефераты по языковедению
Рефераты по юридическим наукам
Рефераты по истории
Рефераты по компьютерным наукам
Рефераты по медицинским наукам
Рефераты по финансовым наукам
Рефераты по управленческим наукам
Психология педагогика
Промышленность производство
Биология и химия
Языкознание филология
Издательское дело и полиграфия
Рефераты по краеведению и этнографии
Рефераты по религии и мифологии
Рефераты по медицине
Реферат: Двойной интеграл в полярных координатах
Реферат: Двойной интеграл в полярных координатах
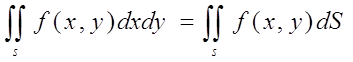 |
Пусть в двойном интеграле
(1)
при обычных предположениях мы желаем перейти к полярным координатам r и f, полагая
x = r cos j, y = r sin j. (2)
![]() Область интегрирования S разобьем на элементарные ячейки DSi с помощью координатных линий r = ri (окружности)
и j = ji (лучи) (рис.1).
Область интегрирования S разобьем на элементарные ячейки DSi с помощью координатных линий r = ri (окружности)
и j = ji (лучи) (рис.1).
 Введем обозначения:
Введем обозначения:
Drj = rj+1 - rj,
Dji = ji+1 - ji
![]()
Так как окружность перпендикулярна (ортогональна) радиусам, то внутренние ячейки DSi с точностью до бесконечно малых высшего порядка малости относительно их площади можно рассматривать как прямоугольники с измерениями rjDji и Drj; поэтому площадь каждой такой ячейки будет равна:
DSi = rj Dji Drj (3)
Что касается ячеек DSij неправильной формы, примыкающих к границе Г области интегрирования S, то эти ячейки не повлияют на значение двойного интеграла и мы их будем игнорировать.
В качестве точки Mij $ Sij для простоты выберем вершину ячейки DSij с полярными координатами rj и ji. Тогда декартовые координаты точки Mij равны:
xij = rj cos ji, yij = rj sin ji.
И следовательно,
f(xij,yij) = f(rj cos ji, rj sin ji) (3')
Двойной интеграл (1) представляет собой предел двумерной интегральной суммы, причем можно показать, что на значение этого предела не влияют добавки к слагаемым
интегральной
суммы, являющиеся бесконечно малыми высшего порядка малости, поэтому учитывая
формулы (3) и (3'), 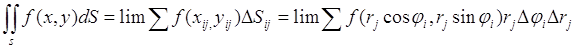
получаем:
(4)
где d - максимальный диаметр ячеек DSij и сумма распространена на все ячейки указанного выше вида, целиком содержащиеся в области S. С другой стороны, величины ji и rj суть числа и их можно рассматривать как прямоугольные декартовые координаты некоторых точек плоскости Ojr. Таким образом, сумма (4) является интегральной суммой для функции
f(r cosj, r sinj)r,
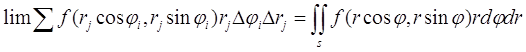 |
соответствующая прямоугольной сетке с линейными элементами Dji и Dri. Следовательно
(5)
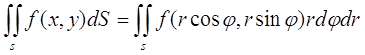
Сравнивая формулы (4) и (5), получим
окончательно
(6)
Выражение
dS = r dj dr
называется двумерным элементом площади в полярных координатах. Итак, чтобы в двойном интеграле (1) перейти к полярным координатам, достаточно координаты x и y заменить по формулам (2), а вместо элемента площади dS подставить выражение (7).
Для вычисления двойного интеграла (6) его нужно заменить повторным. Пусть область интегрирования S определяется неравенствами
Где r1(j), r1(j) - однозначные непрерывные функции на отрезке [a,b]. (рис 2).
Имеем
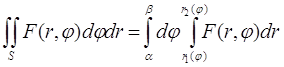
(8)
Где
F(r,j) = rf(r cosj, r sinj)
Пример 1.
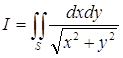 |
Переходя к полярным координатам j и r, вычислить двойной интеграл
![]() Где S - первая четверть круга радиуса R=1, с центром в точке О(0,0) (рис 3).
Где S - первая четверть круга радиуса R=1, с центром в точке О(0,0) (рис 3).
Так как
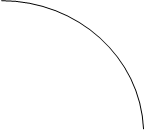
![]()
то применяя формулу (6),

![]()
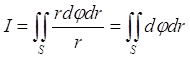
получим
Область S определена
Неравенствами
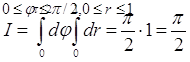
Поэтому на основании формулы (8)
имеем
Пример 2.
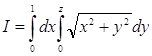 |
В интеграле
(9)
перейти к полярным координатам.
Область интегрирования здесь есть треугольник S, ограниченный прямыми y=0, y=x, x=1 (рис 4).
В полярных координатах уравнения
этих прямых записываются
следующим образом: j=0,
j=p/4, r cosj=1 и,
следовательно, область S
определяется неравенствами
![]()
Отсюда на основании формул
(6) и(8), учитывая, что
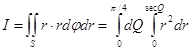 |
|||
имеем
Список литературы
Для подготовки данной работы были использованы материалы с сайта http://www.ed.vseved.ru/