
Рефераты по рекламе
Рефераты по физике
Рефераты по философии
Рефераты по финансам
Рефераты по химии
Рефераты по хозяйственному праву
Рефераты по экологическому праву
Рефераты по экономико-математическому моделированию
Рефераты по экономической географии
Рефераты по экономической теории
Рефераты по этике
Рефераты по юриспруденции
Рефераты по языковедению
Рефераты по юридическим наукам
Рефераты по истории
Рефераты по компьютерным наукам
Рефераты по медицинским наукам
Рефераты по финансовым наукам
Рефераты по управленческим наукам
Психология педагогика
Промышленность производство
Биология и химия
Языкознание филология
Издательское дело и полиграфия
Рефераты по краеведению и этнографии
Рефераты по религии и мифологии
Рефераты по медицине
Курсовая работа: Расчет планетарной коробки переключения передач трактора класса 0,2
Курсовая работа: Расчет планетарной коробки переключения передач трактора класса 0,2
Содержание
1.Тяговый расчет трактора ……………………………………………………...3
1.1. Выбор тягового диапазона………………………………………………….3
1.2. Выбор оптимальных весовых параметров трактора……………...….........3
1.3. Выбор рабочих скоростей и передаточных чисел трансмиссии…............7
1.4. Определение потребной мощности двигателя…………………………….8
1.5. Определение передаточного числа трансмиссии на первой передаче…..8
2. Синтез схем планетарных коробок передач………………………………..10
2.1. Построение обобщенного кинематического плана планетарной коробки передач..……………………………………….………………………………...10
2.2. Составление исходных уравнений и приведение исходных уравнений к простейшему виду ………….…………………………………………………..13
2.3. Составление производных уравнений…………………………………….14
2.4. Проверка составленных уравнений……………………………….……….16
2.5. Отбраковка ТДМ………………………………………………….………...16
2.6. Составление групп уравнений……………………………………….…….20
2.7. Построение структурных схем ТДМ и ПКП……………………….……..21
3. Определение чисел зубьев шестерен в планетарной коробке передач……28
4. Кинематический анализ планетарной коробки передач ………..…….……32
5. Силовой анализ планетарной коробки передач ……………………..……..39
6. Библиографический список…………………………………………………..42
1.Тяговый расчет трактора .
Необходимые тяговые показатели трактора могут быть достигнуты и эффективно использованы только в том случае, если будут правильно выбраны его параметры: вес, скорости движения (передаточные числа трансмиссии) и мощность двигателя.
Исходные данные:
Тип трактора: колесный, сельскохозяйственный 4х2.
Тяговый класс: 0,2.
Трансмиссия: гидромеханическая.
Прототип: отсутствует.
1.1. Выбор тягового диапазона
Тяговые свойства трактора определяются максимальным и минимальным тяговыми усилиями, которые определяют тяговый диапазон.
Так, как трактор данного
тягового класса не связан с тракторами предыдущего тягового класса, то тяговый
диапазон принимаем: ![]() .
.
![]()
где ![]() - расчётное тяговое
усилие на низшей рабочей передаче,
- расчётное тяговое
усилие на низшей рабочей передаче,
здесь ![]() - коэффициент
перегрузки по тяге; по данным НАТИ для колесных сельскохозяйственных тракторов
- коэффициент
перегрузки по тяге; по данным НАТИ для колесных сельскохозяйственных тракторов ![]() , принимаем
, принимаем ![]() .
.
1.2. Выбор оптимальных весовых параметров трактора.
Существующие методики выбора весовых параметров трактора при выполнении тягового расчета позволяют подобрать вес трактора таким образом, чтобы тяговый кпд трактора, работающего с номинальной силой тяги на крюке при установившемся движении на горизонтальном участке пути в определенных почвенных условиях, находился в зоне, близкой к его максимальной величине. Однако трактор – это разносторонняя машина, которая предназначена для выполнения различных сельскохозяйственных и дорожно-транспортных работ, и следовательно, работает в самых разнообразных почвенных условиях. Таким образом, подобранный вес может оказаться неоптимальным, если трактор будет работать в других условиях. В связи с этим возникает необходимость многофакторного подхода к решению задачи выбора весовых параметров трактора при выполнении тягового расчета.
В качестве параметра оптимизации принимаем значение тягового кпд трактора при работе с номинальной силой тяги на крюке в данных почвенных условиях, которое определяется по формуле
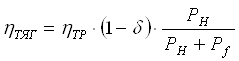
где ηТР - кпд трансмиссии; δ- величина буксования; РН- номинальное тяговое усилие по типажу, kH; Рf- сила сопротивления качению трактора, kH.
Определенное таким образом значение тягового кпд отвечает требованиям, предъявляемым к параметру оптимизации. Однако, используя его как параметр оптимизации, выражение можно упростить. Механический кпд трансмиссии в реальных машинах изменяется в зависимости от нагрузки и угловой скорости ведомых валов. Так как мы рассматриваем значение тягового кпд только в одной точке, то с достаточной степенью точности можно принять ηТР=const и параметр оптимизации представить в виде
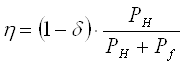
Величина η зависит от буксования δ и силы сопротивления качению Рf, которые при эксплуатации трактора с номинальной силой тяги на крюке на данном почвенном фоне зависят только от веса трактора GЭ. Решая методом последовательных приближений задачу оптимизации, находим экстремальное, в данном случае максимальное, значение параметра η и соответствующее ему значение веса трактора GЭ.
Решение производим в следующей последовательности.
1.2.1. Назначаем область определения фактора GЭ. Область определения эксплуатационного веса GЭ выбираем в соответствии с весом трактора прототипа, на базе которого проектируется новая машина или который она должна заменить:
![]()
где GЭЛ - левая граничная точка области определения фактора GЭ; GЭП - правая граничная точка области определения фактора GЭ.
Множество GЭЛ, GЭП, представляет собой диапазон поиска, который включает граничные точки и точки, расположенные на кратное число шагов от них. Принимаем шаг 0,5 kH. Все дальнейшие расчеты выполняем для каждой точки заданного поиска.
1.2.2. Определяем силу сопротивления качению Рf по формуле
![]()
где f- коэффициент сопротивления качению трактора на данном почвенном фоне.
1.2.3. Определение величины буксования.
Величина φКР, отложенная по оси абсцисс, определяем по формуле
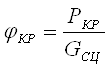
где GСЦ - сцепной вес трактора, рассчитываемый по формуле
![]()
Здесь λ- коэффициент нагрузки ведущих колес; для гусеничных тракторов и колесных тракторов 4К4 λ=1, для колесных 4К2 λ=0,8).
Для решения задачи с помощью ЭВМ каждую кривую δ=δ(φКР) аппроксимируем двумя прямыми линиями вида a+b·φКР и с+d·φКР. Коэффициенты a, b, c, d подбираем из условия максимального приближения к кривой δ=δ(φКР).
Коэффициенты аппроксимации кривых буксования δ=δ(РКР).
Таблица 1
| Тип трактора | Вид почвенного фона | f | a | B | C | d |
φКР |
| Колёсный | Стерня | 0,1 | 0 | 0,2 | -0,6 | 1,44 | 0,5 |
| Поле, подготовленное под посев | 0,18 | 0,03 | 0,4 | -0,3 | 1,5 | 0,3 | |
| Грунтовая дорога | 0,05 | 0 | 0,11 | -0,5 | 0,96 | 0,58 | |
| Бетонная или асфальтовая дорога | 0,02 | 0 | 0,11 | -0,96 | 1,55 | 0,64 |
1.2.4. Определяем величину параметра оптимизации.
Сравнивая каждую последующую, определенную таким образом величину с предыдущей, находим максимальное значение параметра оптимизации, фиксируем эксплуатационный вес трактора, соответствующий этой максимальной величине.
1.2.5. Найденное значение эксплуатационного веса является оптимальным для трактора, работающего в данных условиях. Для того чтобы найти оптимальное значение эксплуатационного веса трактора, работающего в различных почвенных условиях, необходимо в зависимости от назначения проектируемого трактора или, ориентируясь на трактор-прототип, проанализировать условия его эксплуатации и определить вероятность работы проектируемого трактора на различных почвенных фонах. Конечным результатом этой части работы является выбор количества почвенных фонов, на которых эксплуатируется трактор, и определение вероятности (Рi) его работы на каждом из них.
Таблица 2
| № | Вид почвенного фона |
|
|
| 1 | Поле, подготовленное под посев | 0,18 | 0,12 |
| 2 | Стерня | 0,1 | 0,05 |
| 3 | Грунтовая дорога | 0,05 | 0,21 |
| 4 | Бетонная или асфальтовая дорога | 0,02 | 0,62 |
Вводим подготовленные данные в программу TTOPT
Таблица 3
| Обозначение в программе | Обозначение в формулах | 1 | 2 | 3 | 4 | |
| Коэффициент сопротивления качению | A1 |
|
0,18 | 0,1 | 0,05 | 0,02 |
| 1-ый коэффициент аппроксимации | A2 |
|
0,03 | 0 | 0 | 0 |
| 2-ый коэффициент аппроксимации | A3 |
|
0,4 | 0,2 | 0,11 | 0,11 |
| 3-ий коэффициент аппроксимации | A4 |
|
-0,3 | -0,6 | -0,5 | -0,96 |
| 4-ый коэффициент аппроксимации | A5 |
|
1,5 | 1,44 | 0,96 | 1,55 |
| Точка излома | A6 |
|
0,3 | 0,5 | 0,58 | 0,64 |
| Вероятность работы на данном почвенном фоне | A7 |
|
0,3 | 0,3 | 0,2 | 0,2 |
|
Левая граничная точка области
определения фактора |
GEL |
|
2 | 2 | 2 | 2 |
| Коэффициент загрузки ведущих колес | RL |
|
0,8 | 0,8 | 0,8 | 0,8 |
| Номинальное тяговое усилие | PN |
|
2 | 2 | 2 | 2 |
|
Правая граничная точка области
определения фактора |
GEP |
|
80 | 80 | 80 | 80 |
Результат работы программы
| Оптимальный КПД | OPTIM |
|
0,49 | 0,72 | 0,85 | 0,92 |
| Оптимальный эксплуатационный вес | GEOPT |
|
9,3 | 5,8 | 5,1 | 4,9 |
| ZWESA |
|
2,5 | 1,5 | 1,2 | 1,0 |
Рассчитав с помощью
программы TTOPT оптимальный вес трактора в различных
почвенных условиях, величину эксплуатационного веса трактора ![]() определяем по формуле:
определяем по формуле:
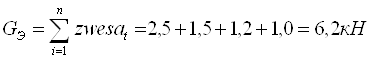 ;
;
1.3. Выбор рабочих скоростей и передаточных чисел трансмиссии.
Диапазон передач должен охватывать скорости и тяговые усилия, определяемые характером выполняемых трактором операций. Различают диапазоны скоростей:
· замедленных или вспомогательных для получения особо низких скоростей движения, которые обуславливаются операциями технологического процесса;
· основных рабочих скоростей, на которых выполняется большинство сельскохозяйственных операций;
· транспортных скоростей, применяемых для перевозки грузов и холостых переездов.
В тяговом расчете осуществляем выбор скоростей и передаточных чисел только диапазона основных рабочих скоростей.
Диапазон основных рабочих скоростей определяем по формуле
![]()
где γg min- минимально допустимый коэффициент загрузки двигателя на высшей передаче; γg min=0,85- для проектируемых сельскохозяйственных тракторов общего назначения.
При проектировании
тракторов низшая основная рабочая скорость ![]() принимается в пределах
принимается в пределах ![]() , выбираем
, выбираем ![]()
Ряд основных скоростей трактора строим по принципу геометрической прогрессии, которая предполагает одинаковую степень изменения загрузки двигателя при переходе с одной передачи на другую. Основное уравнение ряда скоростей имеет следующий вид:
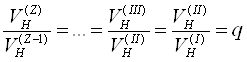 ;
;
где q- знаменатель геометрической прогрессии, определяемый формулой
![]()
Здесь Z=4 - число основных передач, которое выбираем по базовому трактору; VН(z)- скорость на высшей рабочей передаче.
![]()
![]()
![]()
![]()
1.4. Определение потребной мощности двигателя.
Номинальная мощность
двигателя ![]() находится
из условия реализации расчетного тягового усилия
находится
из условия реализации расчетного тягового усилия ![]() на заданной низшей рабочей
скорости
на заданной низшей рабочей
скорости ![]() :
:
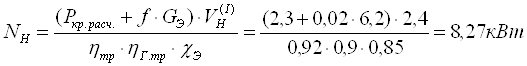
По потребной мощности выбираем двигателя: с номинальной мощностью
10 кВт.
1.5. Определение передаточного числа трансмиссии на первой передаче.
Число передач коробки передач принимаем равным пяти, а чтобы улучшить перекрытие между ступенями, совмещается точка Ркр.рас с точкой гидротрансформатора, имеющей ηг мах, а точка перехода на высшую передачу – в момент перехода на режим гидромуфты.
Передаточное число трансмиссии на I передаче ίТР(1).
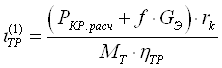
![]()
где f- коэффициент
сопротивления качению на наиболее вероятном почвенном фоне, встречающемся при
эксплуатации трактора, в нашем случае для поля подготовленного под посев f=0,02; Мт – момент
совместной работы двигателя и гидротрансформатора в режиме ηг max.; rk- динамический радиус колеса, м; ![]() - механический
КПД трансмиссии, который включает внутренние потери в ходовой системе: для
сельскохозяйственных колесных тракторов
- механический
КПД трансмиссии, который включает внутренние потери в ходовой системе: для
сельскохозяйственных колесных тракторов ![]() , принимаем
, принимаем ![]() ; КПД
гидротрансформатора
; КПД
гидротрансформатора ![]() = 0,87 .
= 0,87 .
![]()
Для колесного трактора
класса 0,2 ![]() .
.
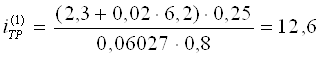
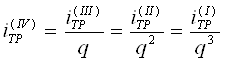
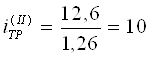
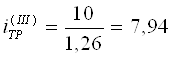
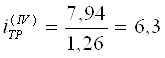
Принимая U5 = 1, находим передаточные числа на остальных передачах планетарной коробки передач: U1 = 2,52; U2 = 2; U3 = 1,6; U4 = 1,26.
2. Синтез схем планетарных коробок передач
2.1. Построение обобщенного кинематического плана планетарной коробки передач
Синтез схем ПКП выполняется в следующей последовательности.
В курсовой работе рассматривается пятиступенчатая ПКП с двумя степенями свободы, обеспечивающая пять передач переднего хода.
Используя уравнение кинематики ТДМ [1, 2.8], построим обобщенный кинематический план ПКП (ОКП ПКП). Он представляет собой графическую зависимость частот вращения центральных звеньев np, ПКП от частоты вращения ведомого вала nвм при постоянной частоте вращения ведущего вала пещ, принятой за единицу:
np=f(nвм) при nвщ=1 .
Подставив в уравнение [1, 2.8] nвщ=1, получим
![]() [1,2.9]
[1,2.9]
Из полученного выражения видно, что зависимость nр = f(nвм) имеет линейный характер и на ОКП ПКП представляется прямой линией. Построить эту зависимость можно по двум точкам.
Первую точку определим для режима блокировки всех звеньев ПКП, при котором
![]()
Для ПКП планы скоростей всех тормозных звеньев должны пройти через точку с координатами (1; 1).
Вторую точку на ОКП ПКП найдем при включенной р передаче, когда в уравнении [1,2.9] np = 0. В результате частота вращения ведомого вала
![]()
Эта точка на плане имеет
координаты 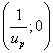 .
.
Таким образом график
зависимости np=f(nвм) на ОКП ПКП представляет собой
прямую, проходящую через точки с координатами (1; 1), ![]() . Первая точка (1; 1) физически
означает, что механизм сблокирован и частоты вращения всех центральных звеньев
ПКП равны частоте вращения ведущего вала, принятой за единицу (
. Первая точка (1; 1) физически
означает, что механизм сблокирован и частоты вращения всех центральных звеньев
ПКП равны частоте вращения ведущего вала, принятой за единицу (![]() ). Вторая точка
). Вторая точка ![]() определяется
для случая остановки тормозного звена np = 0.
определяется
для случая остановки тормозного звена np = 0.
Она определяет частоту
вращения ведомого вала ПКП при включенной р передаче (![]() ).
).
Частота вращения ведущего
вала (![]() ) на
ОКП ПКП представляется прямой, проходящей через точку (1; 1) параллельно оси
абсцисс.
) на
ОКП ПКП представляется прямой, проходящей через точку (1; 1) параллельно оси
абсцисс.
При разбивке передаточных чисел между агрегатами трансмиссии, с целью упрощения конструкции ПКП, предусматриваем в ней прямую передачу с передаточным числом uр = 1. Это уменьшает на единицу число ТДМ, входящих в схему ПКП. Необходимо, чтобы прямой была наиболее часто используемая передача, так как КПД такой передаче близок к единице.
ОКП для передаточных чисел проектируемой ПКП представлены на рис. 1. Этот план является общим для любых схем ПКП, реализующих заданные передаточные числа. Он позволяет определить абсолютные и относительные частоты вращения центральных звеньев ПКП на нейтрали и на всех передачах. Частота вращения ведомого вала nвм выражается отрезками оси абсцисс или ординатами штрихпунктирного луча, проведенного через начало координат и единичную точку. Частоты вращения тормозных звеньев nр на включаемых передачах и нейтрали определяются ординатами их лучей.
Относительные частоты вращения центральных звеньев определяются вертикальными отрезками между их лучами.
Относительная частота вращения максимальна на первой передаче между ведущим звеном nвщ и n4.

Рис. 1. ОКП ПКП для заданных передаточных чисел
Высокие относительные частоты вращения центральных звеньев могут привести к недопустимо большим частотам вращения подшипников сателлитов. Здесь необходимо отметить, что предельная быстроходность подшипников качения ограничивается в каталоге предельной частотой вращения колец. Под предельной быстроходностью подшипника понимается наибольшая частота вращения колец, за пределами которой расчетная долговечность подшипника не гарантируется.
Кроме основных кинематических параметров ОКП ПКП позволяет определить моменты блокировочных фрикционов при различных вариантах блокировки звеньев для получения прямой передачи.
2.2. Составление исходных уравнений и приведение исходных уравнений к простейшему виду
Для этого используется уравнение [1, 2.8]. В результате получим четыре исходных уравнения:
![]()
![]()
![]()
![]()
В приведенных уравнениях [1, 2.4-2.6] наименьший коэффициент равен плюс единице и коэффициенты при частотах вращения центральных звеньев располагаются в порядке возрастания по абсолютной величине.
Уравнения 1и 2 по своей структуре полностью соответствуют уравнениям [1, 2.4-2.6]. Поэтому перепишем их без изменения.
![]()
![]()
В уравнении 3 и 4 коэффициенты при частотах вращения n2, n3, n4 меньше единицы. Для приведения данных уравнений к простейшему виду разделим их соответственно на 0,6 и 0,26 и перепишем в порядке возрастания по абсолютной величине коэффициентов при частотах вращения центральных звеньев. В результате получим
![]()
![]() .
.
2.3. Составление производных уравнений
Производные уравнения отличаются от исходных и друг от друга комбинацией входящих в уравнения частот вращения центральных звеньев.
Общее число исходных и производных уравнений W определяется числом возможных сочетаний из общего числа частот вращения тормозных звеньев р , ведущего и ведомого звеньев (всего р + 2 звена) по три, так как в каждое уравнение входят частоты вращения трех центральных звеньев ТДМ.
В общем виде
![]()
В рассматриваемом примере р = 4 . Тогда
![]()
Следовательно, к четырем исходным уравнениям надо добавить 16 производных.
Первая группа производных уравнений получается исключением из исходных уравнений частоты вращения ведомого звена nвм. Для этого рассматриваются попарно два уравнения. При этом из четырех уравнений
![]()
Следовательно, из четырех исходных уравнений исключением из них частоты вращения ведомого звена можно получить следующее число комбинаций по два уравнения nвм можно получить 6 производных уравнений.
Для исключения из уравнений 1 и 2 nвм умножаем уравнение 2 на (-2,52/2) и суммируем его с уравнением 1. В результате получим уравнение
![]()
Остальные пять производных уравнений получены аналогично:
![]() (из уравнений 1 и 3);
(из уравнений 1 и 3);
![]() (из уравнений 1 и 4);
(из уравнений 1 и 4);
![]() (из уравнений 2 и 3);
(из уравнений 2 и 3);
![]() (из уравнений 2 и 4);
(из уравнений 2 и 4);
![]() (из уравнений 3 и 4).
(из уравнений 3 и 4).
После приведения полученных уравнений к простейшему виду получим:
![]()
![]()
![]()
![]()
![]()
![]()
Вторая группа производных уравнений получается исключением из исходных уравнений 1-4 частоты вращения ведущего звена nвщ.
Здесь, как и в ранее рассмотренном случае, из четырех исходных уравнений исключением из них частоты вращения ведущего звена nвщ можно получить 6 производных уравнений:
![]() (из уравнений 1 и 2);
(из уравнений 1 и 2);
![]() (из уравнений 1 и 3);
(из уравнений 1 и 3);
![]() (из уравнений 1 и 4);
(из уравнений 1 и 4);
![]() (из уравнений 2 и 3);
(из уравнений 2 и 3);
![]() (из уравнений 2 и 4);
(из уравнений 2 и 4);
![]() (из уравнений 3 и 4).
(из уравнений 3 и 4).
После приведения полученных уравнений к простейшему виду получим:
![]()
![]()
![]()
![]()
![]()
![]()
Остальные недостающие четыре уравнения определим из уравнений 5-10 исключением из них частоты вращения ведущего звена nвщ или из уравнений 11-16 исключением из них частоты вращения ведомого звена nвм. В результате получим:
![]() (из уравнений 11 и 12);
(из уравнений 11 и 12);
![]() (из уравнений 12 и 16);
(из уравнений 12 и 16);
![]() (из уравнений 14 и 15);
(из уравнений 14 и 15);
![]() (из уравнений 11 и 15).
(из уравнений 11 и 15).
После приведения полученных уравнений к простейшему виду имеем:
![]()
![]()
![]()
![]()
2.4. Проверка составленных уравнений
Уравнения проверяются по следующим параметрам. Наименьший коэффициент при частоте вращения центрального звена в каждом уравнении должен быть равен единице. Наибольший по абсолютной величине коэффициент должен быть на единицу больше среднего. Комбинация частот вращения центральных звеньев, входящих в каждое уравнение, не должна повторяться.
В данном случае все уравнения 1-20 отвечают выше перечисленным требованиям.
Все полученные уравнения переносятся в табл. 1, в которой предусматривают колонки 3, 4, 5 и 6 для записи характеристик ТДМ, относительных максимальных частот вращения сателлитов, структурных схем ТДМ и общей оценки механизма.
2.5. Отбраковка ТДМ
Отбраковка ТДМ по величине характеристики планетарного ряда к. Для схем ТДМ со смешанным зацеплением шестерен характеристика планетарного ряда может изменяться в пределах 1,5 < к < 4,0 (4,5).
Для синтеза схем ПКП будем использовать только ТДМ со смешанным зацеплением шестерен, для которых 1,5 < к < 4,0.
Тогда по величине характеристики планетарного ряда к в табл. 3 отбраковываем уравнения 1, 2, 3, 5, 8, 9, 10, 13, 15, 16, 17 и 20 (см. графу 3 и 6 таблицы).
Отбраковка ТДМ по величине относительных частот вращения сателлитов пВо. Здесь рассматриваются только механизмы, у которых характеристика планетарного ряда к находится в приемлемых пределах.
Для схемы ТДМ со смешанным зацеплением шестерен относительные частоты вращения сателлитов определяются, как и в простой передаче при неподвижном водиле.
Таблица 3
Анализ схем ТДМ на возможность дальнейшего использования
| № | Уравнение кинематики ТДМ | К |
|
Структурная схема | Примечание | ||
| 1 | 2 | 3 | 4 | 5 | 6 | ||
| 1 |
|
1,12 | Исключить по К | ||||
| 2 |
|
1 | Исключить по К | ||||
| 3 |
|
1,33 | Исключить по К | ||||
| 4 |
|
3,85 | 4,2 | Годное | |||
| 5 |
|
4,85 | Исключить по К | ||||
| 6 |
|
1,63 | 3,15 | Годное | |||
| 7 |
|
1,92 | 1,64 | Годное | |||
| 8 |
|
4,02 | Исключить по К | ||||
| 9 |
|
1,37 | Исключить по К | ||||
| 10 |
|
1,22 | Исключить по К | ||||
| 11 |
|
1,9 | 1,37 | Годное |
|
||
| 12 |
|
1,54 | 2,25 | Годное |
|
||
| 13 |
|
4,76 | Исключить по К |
|
|||
| 14 |
|
1,5 | 2,4 | Годное |
|
||
| 15 |
|
2,86 | 1,86 | Годное |
|
||
| 16 |
|
1,33 | Исключить по К |
|
|||
| 17 |
|
1,26 | Исключить по К |
|
|||
| 18 |
|
2,17 | 1,57 | Годное |
|
||
| 19 |
|
3,29 | 0,9 | Годное |
|
||
| 20 |
|
8,34 | Исключить по К |
|
|||
Относительные частоты вращения сателлитов nВо определяем по одному из выражений [1, 2.11-2.13]. При этом nВо определяем для той передачи, на которой они максимальные, а максимальные они там, где относительные частоты центральных звеньев наибольшие. В нашем случае, в соответствии с ОКП ПКП (см рис. 1), наибольшие относительные частоты вращения центральных звеньев на первой передаче.
Абсолютные частоты вращения центральных звеньев ПКП для данной передачи определим из ОКП ПКП (рис. 1).
Здесь:
![]() ;
; 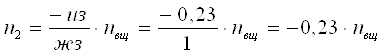 ;
;
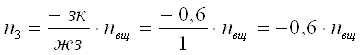 ;
;
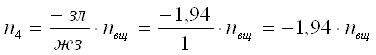 ;
;
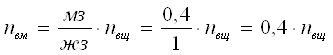 ;
;
Для четвертого ТДМ из
табл. 3 для определения nВо используем выражение [1, 2.11].
Здесь ![]() ;
; ![]() ;
; ![]() .
.
Подставляя эти значения в выражение [1,2.11], получим
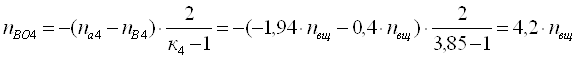 Значение
Значение ![]() по абсолютной величине для уравнения 4 заносим в графу
4 табл. 1.
по абсолютной величине для уравнения 4 заносим в графу
4 табл. 1.
Для шестого ТДМ из табл.
3 для определения nВо используем выражение [1, 2.13].
Здесь ![]() ;
; ![]() ;
; ![]() ;
; ![]() . Подставляя
эти значения в выражение [1, 2.13], получим
. Подставляя
эти значения в выражение [1, 2.13], получим
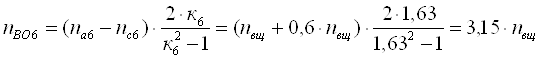
Для седьмого ТДМ из табл.
3 для определения nВо используем выражение [1, 2.13].
Здесь ![]() ;
; ![]() ;
; ![]() ;
; ![]() . Подставляя
эти значения в выражение [1, 2.13], получим
. Подставляя
эти значения в выражение [1, 2.13], получим
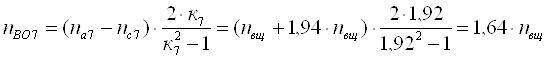
Для одиннадцатого ТДМ из
табл. 3 для определения nВо используем выражение [1, 2.11].
Здесь ![]() ;
; ![]() ;
; ![]() ;
; ![]() . Подставляя
эти значения в выражение [1, 2.11],
получим
. Подставляя
эти значения в выражение [1, 2.11],
получим

Для двенадцатого ТДМ из
табл. 3 для определения nВо используем выражение [1,2.13]. Здесь
![]() ;
; ![]() ;
; ![]() ;
; ![]() .Подставляя
эти значения в выражение [1, 2.13], получим
.Подставляя
эти значения в выражение [1, 2.13], получим
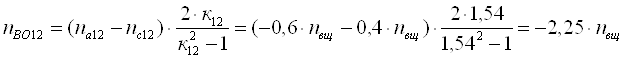
Для четырнадцатого ТДМ из
табл. 3 для определения nВо используем выражение [1,2.13]. Здесь
![]() ;
; ![]() ;
; ![]() ;
; ![]() . Подставляя
эти значения в выражение [1,2.13], получим
. Подставляя
эти значения в выражение [1,2.13], получим
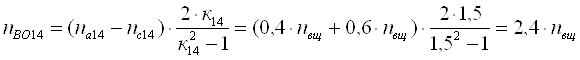
Для пятнадцатого ТДМ из
табл. 3 для определения nВо используем выражение [1,2.13].
Здесь: ![]() ;
;
![]() ;
; ![]() ;
; ![]() . Подставляя
эти значения в выражение [1,2.13], получим
. Подставляя
эти значения в выражение [1,2.13], получим
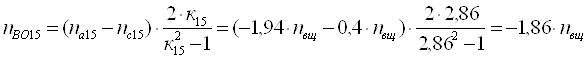 Для восемнадцатого ТДМ из табл. 3
для определения nВо используем выражение [1,2.13]. Здесь
Для восемнадцатого ТДМ из табл. 3
для определения nВо используем выражение [1,2.13]. Здесь
![]() ;
; ![]() ;
; ![]() ;
; ![]() . Подставляя
эти значения в выражение [1,2.13], получим
. Подставляя
эти значения в выражение [1,2.13], получим
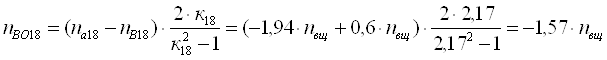
Для девятнадцатого ТДМ из
табл. 3 для определения nВо используем выражение [1,2.13]. Здесь
![]() ;
; ![]() ;
; ![]() ;
; ![]() .. Подставляя
эти значения в выражение [1,2.13], получим
.. Подставляя
эти значения в выражение [1,2.13], получим
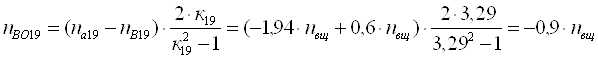
При выборе ТДМ для составления схемы ПКП одним из основных ограничений является предельная относительная частота вращения nВо сателлитов, которая должна удовлетворять условию нормальной работы подшипниковых узлов в течение заданного срока службы машины.
Применяемые для сателлитов серийные подшипники качения допускают под нагрузкой относительную частоту вращения колец nВо до 6000 мин-1, а без нагрузки - до 10000 мин-1. Поэтому, при nВо < 6000 мин-1 уравнение кинематики ТДМ считается годным для дальнейшего исследования, при 6000≤nВо≤10000 мин-1 - условно годным, а при nВо>10000 мин-1 - негодным.
Условно годные ТДМ используются, если на передаче с максимальными относительными частотами вращения сателлитов они работают без нагрузки. Установить, как нагружен механизм, можно только после построения схемы ПКП.
Для исследуемой схемы ПКП частота вращения ведущего вала nвщ = 2000 мин-1. Тогда годными являются уравнения 7, 11, 12, 14, 15, 18 и 19 (см. графу 4 и 6 табл. 1).
Искомая схема ПКП должна
включать четыре ТДМ, так как она должна обеспечивать получение четырех передач
с передаточными числами ![]() .
.
2.6. Составление групп уравнений
Из семи уравнений, куда
входят годные 7, 11, 12, 14, 15, 18 и 19 уравнения, описывающие соответствующие
ТДМ, нужно составить различные комбинации по четыре уравнения в группе, так как
в ПКП четыре передачи с передаточными числами ![]() :
:
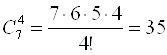
Следовательно, можно
составить 35 неповторяющихся групп уравнений по четыре уравнения в каждой
группе. Возможные комбинации групп уравнений приведены в табл. 4. Из
составленных неповторяющихся комбинаций групп уравнений отбраковываем группы, в
которых каждая из р + 2 частот
вращения центральных звеньев не встречается хотя бы один раз. Следовательно,
для составления схемы ПКП с заданными передаточными числами в каждой группе
уравнений должны присутствовать частоты вращения ![]() тормозных звеньев, а также
частота вращения ведущего nвщ и ведомого nвм звеньев. По признаку отсутствия какого-либо из перечисленных
звеньев отбраковываем 14 групп уравнений (в табл. 4 отмечены курсивом).
тормозных звеньев, а также
частота вращения ведущего nвщ и ведомого nвм звеньев. По признаку отсутствия какого-либо из перечисленных
звеньев отбраковываем 14 групп уравнений (в табл. 4 отмечены курсивом).
Таблица №4
| 7.11.12.14 | 7.11.12.15 | 7.11.12.18 | 7.11.12.19 | 7.11.14.15 |
| 7.11.14.18 | 7.11.14.19 | 7.11.15.18 | 7.11.15.19 | 7.11.12.15 |
| 7.11.14.15 | 7.12.14.18 | 7.12.14.19 | 7.12.14.15 | 7.12.15.18. |
| 7.12.15.19 | 7.12.18.19 | 7.14.15.18 | 7.14.15.19. | 7.12.14.18 |
| 7.12.15.18. | 7.15.18.19 | 7.14.18.19 | 11.12.15.19 | 11.12.18.19. |
| 11.14.15.19 | 11.14.18.19 | 11.12.15.18 | 11.12.14.18 | 11.12.14.15. |
| 11.12.15.19 | 11.12.15.18 | 11.12.14.15. | 11.12.14.19 | 11.15.18.19 |
Более компактная конструкция ПКП получается, если характеристики к планетарных механизмов, составляющих группу уравнений, достаточно близки по величине. Поэтому структурные схемы ПКП строим только для тех групп уравнений, в которых характеристика к отличается не более чем на единицу (см. табл. 4). В табл. 4 эти группы уравнений выделены жирным шрифтом с подчеркиванием (13 групп).
2.7. Построение структурных схем ТДМ и ПКП
Рассмотрим из табл. 3 годное уравнение 7 кинематики ТДМ:
![]()
В данном уравнении солнечная шестерня является ведущим звеном с частотой вращения nвщ, эпициклическая шестерня - тормозным звеном с частотой вращения n2, а водило - тормозным звеном с частотой вращения n1.
Перенесем структурную схему для уравнения 7 кинематики ТДМ в графу 5 табл. 3. Аналогично сроим структурные схемы для оставшихся годных уравнений и переносим в табл. 3. При этом у каждого звена на структурной схеме ставим индекс, указывающий, с каким тормозным звеном (1, 2, 3, 4), ведущим (вщ) или ведомым (вм) валом это звено соединяется.
Из выделенных 13 групп уравнений (см. табл. 4) удалось построить 6 структурных схем ПКП, приведенных на рис. 2.
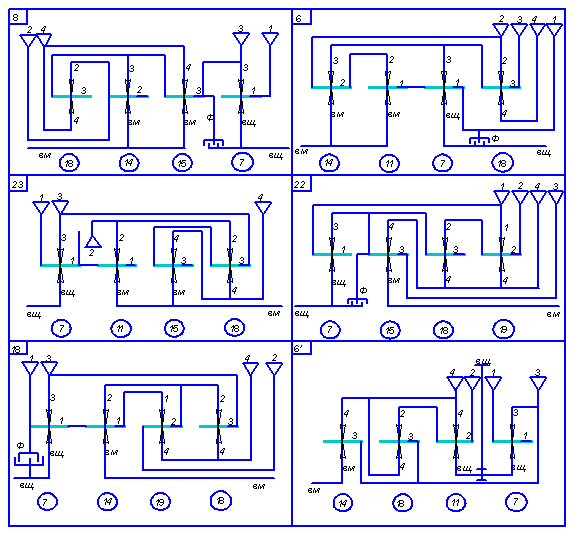
Рис. 2. Структурные схемы ПКП
Выбор структурной схемы ПКП производим:
- по обеспечению требований компоновки ПКП в машине;
- по минимальной слоистости валов;
- по возможности оптимальной установки блокировочного фрикциона для включения прямой передачи;
- по обеспечению максимального КПД ПКП.
Требования компоновки. Какое взаимное расположение ведущего и ведомого валов ПКП наиболее целесообразно, зависит от принятой общей схемы компоновки трансмиссии. Требованиям компоновки трансмиссии удовлетворяют схемы с соосным размещением ведущего и ведомого валов, т.е. схемы 6, 23, 18, 8 и 22 на рис. 2. Однако в схемах 18, 8 и 22 невозможно обеспечить работу ПКП на всех передачах, поэтому для дальнейшего рассмотрения принимаем схемы 6 и 23.
Установка блокировочного фрикциона. В соответствии с ОКП ПКП (см. рис. 1) наименьший расчетный момент блокировочного фрикциона получается при блокировке на нейтрали ведущего звена с тормозным звеном четвертой передачи:
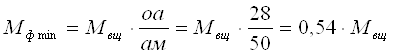
В оставшихся для дальнейшего анализа схемах 6, 23, 18, 8 и 22 (см. рис. 2) такую блокировку выполнить невозможно.
В схемах 6, 23 наименьший из возможных расчетный момент блокировочного фрикциона получается при блокировке ведущего звена (вщ) с тормозным звеном (1) первой передачи. Здесь расчетный момент блокировочного фрикциона
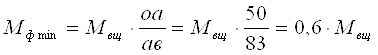
Следовательно, по обеспечению минимального расчетного момента блокировочного фрикциона структурные схемы 6, 23 ПКП идентичны. На указанных структурных схемах (см. рис. 2) блокировочные фрикционы, блокирующие ведущее и тормозное звено первой передачи, обозначены буквой Ф. Однако в схеме 6’ затруднен вывод тормозного звена второй передач, поэтому для дальнейшего рассмотрения принимаем схему 6.
Определение КПД ПКП. При выборе схемы ПКП КПД определяется на наиболее часто используемой передаче, не считая прямую. Для определения КПД ПКП удобен метод, предложенный проф. М. А. Крейнесом.
Общая методика определения КПД ПКП на любой включенной передаче представлена в виде следующих этапов:
1) по кинематической схеме ПКП с использованием уравнений кинематики ТДМ определяем кинематическое передаточное число uр на р передаче (см. выражение 2.19);
2) по выражению [1, 2.21] определяем знаки показателей степени хi у η0;
3) по выражению [1, 2.20]
определяем силовое передаточное число ![]() на р передаче;
на р передаче;
4) по выражению [1, 2.18] определяем КПД ПКП ηр на р передаче.
Принимаем, что наиболее часто используемой будет вторая передача, которая реализуется при торможении второго тормозного звена с частотой вращения n2 .
Аналитическое определение кинематического передаточного числа ПКП.
а). На структурной схеме ПКП выделяем работающие (нагруженные) на рассматриваемой передаче планетарные ряды. Не нагружены те ряды, в которых хотя бы одно звено свободно.
В схеме 23 (рис. 2) не нагружен планетарный ряд 18, у которого свободно водило, соединенное с выключенным тормозом (4) четвертой передачи. Планетарные ряды 7, 11 и 14 нагружены.
б). Для каждого работающего (нагруженного) планетарного ряда составляем уравнение кинематики, выраженное через характеристику к ряда /см. выражение (2.4)/. В нашем случае для 7, 11 и 14 планетарных рядов (рис. 2) уравнения кинематики имеют вид:
![]()
![]() [1,2.22]
[1,2.22]
![]()
в). Составляем уравнения связи. Уравнения связи составляем на основании кинематической или структурной схемы 6 ПКП (см. рис. 2). Из представленной схемы ПКП следует, что
nв7= nв11; nа7=nвщ; nа11= nа14=nвм; nс14= nс7= nв18; nв14= nс11= nс18=0.
г). В уравнениях кинематики и связи частоты вращения всех звеньев, связанных с ведущим и ведомым валами, заменяются на nвщ и nвм . В результате уравнения кинематики [1,2.22] примут вид:
![]()
![]() [1,2.23]
[1,2.23]
![]()
д). Для определения
передаточного числа ПКП на второй передаче ![]() решаем систему уравнений [1,2.23].
Сначала из второго и третьего уравнений полученной системы уравнений [1,2.23]
определяем
решаем систему уравнений [1,2.23].
Сначала из второго и третьего уравнений полученной системы уравнений [1,2.23]
определяем
![]()
![]()
Поскольку ![]() и
и ![]() , то приравняв эти
уравнения получим
, то приравняв эти
уравнения получим
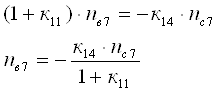
В итоге
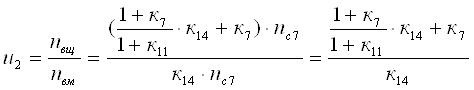
е). Для проверки
выполненных аналитических выкладок в полученное уравнение из табл. 3
подставляем значения характеристик планетарных рядов ![]()
![]()
![]() . В результате получим
. В результате получим
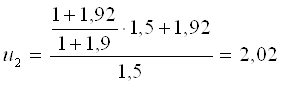
Так как полученное выражение u2 равно заданному, то вывод выражения выполнен правильно.
Определение знаков показателей степени хi b η0.
Для структурной схемы 5 ПКП согласно выражению [1,2.25],

Тогда, используя выражение [1,2.21],

Аналогично определяем


Силовое передаточное число на второй передаче определяем по выражению [1,2.20]. Тогда для структурной схемы 5 имеем
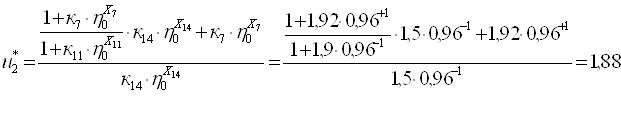
Определение КПД ПКП на второй передаче. Для структурной схемы 5 ПКП
На рис. 3 приведена кинематическая схема ПКП, выполненная по структурной схеме 6 (см. рис. 2). Тормозом Т1 включается первая передача. В этом случае под нагрузкой работают планетарные ряды 7, 11 и 14. Тормозом Т2 включается вторая передача. В этом случае под нагрузкой работают планетарные ряды 7, 11 и 14. Тормозом Т3 включается третья передача. В этом случае под нагрузкой работают планетарные ряды 7, 11 и 14. Тормозом Т4 включается четвертая передача. В этом случае под нагрузкой работают планетарные ряды 7, 11, 14 и 18. Фрикционом Ф включается пятая (прямая) передача.
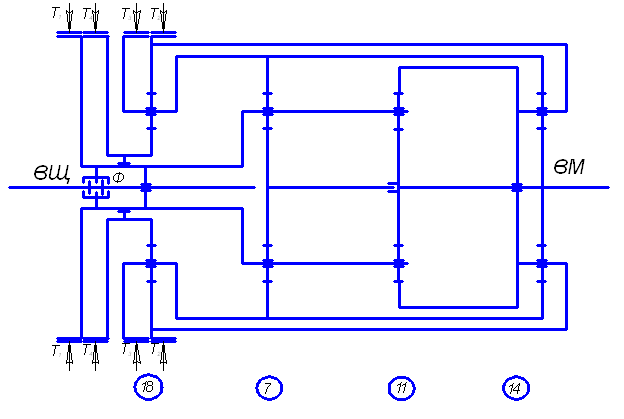
Рис. 3. Кинематическая схема ПКП
Таким образом, используя метод синтеза ПКП, выбрали наиболее рациональную ее кинематическую схему.
3. Определение чисел зубьев шестерен в планетарной коробке передач
В ТДМ, которые относятся к соосным зубчатым механизмам, нельзя произвольно назначать числа зубьев шестерен, так как необходимо, прежде всего, обеспечить совпадение осей вращения их центральных звеньев. Кроме того, при наличии нескольких сателлитов необходимо обеспечить возможность сборки механизма, а также отсутствие задевания сателлитов одного ряда друг за друга. При этом число зубьев наименьшей шестерни ТДМ должно исключать вероятность подрезания ножки зуба.
Таким образом, при подборе чисел зубьев шестерен ТДМ необходимо обеспечить соблюдение условий соосности, сборки и соседства.
Условие соосности. Выполнение этого условия обеспечивает соосность центральных зубчатых колес ТДМ. Для наиболее компактного и самого распространенного в схемах ПКП одновенцового ТДМ со смешанным зацеплением шестерен условие соосности записывается в виде:
m Zс = mZa +2 m ZB0,
где m - модуль зацепления; Zс, Za, ZB0- число зубьев соответственно солнечной шестерни, эпицикла и сателлита.
Так как модуль у всех шестерен одинаков, то
Zc=Za+2ZBo. [1,2.29]
Из условия соосности [1,2.29] вытекает важное практическое правило при подборе числа зубьев: солнечная шестерня и эпицикл должны иметь или четное или нечетное число зубьев, чтобы их разность была четной величиной. В противном случае сателлиты будут иметь дробное число зубьев.
Условие сборки. Это условие определяет возможность сборки ТДМ, т. е. возможность одновременного зацепления сателлитов с центральными зубчатыми колесами.
Рассмотрим в качестве примера одновенцовый ТДМ со смешанным зацеплением шестерен [1, рис. 2.1, а], у которого сателлит В должен одновременно находиться в зацеплении с солнечной шестерней а и эпициклом с. Это возможно только при условии, когда
![]() [1,2.30]
[1,2.30]
где d- число сателлитов; γ- любое целое число.
Таким образом, условие сборки одновенцового ТДМ со смешанным зацеплением шестерен заключается в том, что сумма чисел зубьев солнечной шестерни и эпицикла должна быть кратна числу сателлитов.
Условие соседства. Выполнение этого условия исключает задевание сателлитов друг о друга и чрезмерные потери мощности на '"барботаж" масла (зазор между вершинами зубьев двух соседних сателлитов должен быть более 3...5 мм). Условие соседства чаще всего проверяют графически. Установлено, что для обеспечения зазора между вершинами зубьев сателлитов более 3...5 мм зазор между их начальными окружностями должен быть не менее 0,2 диаметра начальной окружности наименьшей шестерни планетарного ряда.
Подбор чисел зубьев необходимо начинать с наименьшей шестерни, число зубьев которой должно быть не менее 12-14. Таким образом, Zmn =12-14, что исключает вероятность подрезания ножки зуба.
В ТДМ со смешанным зацеплением шестерен и одновенцовыми сателлитами [1, рис. 2.1, а] в зависимости от характеристики к ряда меньшее число зубьев может иметь солнечная шестерня или сателлит.
Если характеристика планетарного ряда к > 3, то Zmin - на солнечной шестерне. Тогда из условия сборки [1,2.30]
![]() [1,2.31]
[1,2.31]
Если к < 3, то Zmin - на сателлите. Тогда из условия соосности
![]() [1,2.32]
[1,2.32]
Подставляя Za из выражения [1,2.31] в [1,2.32], получим
![]() [1,2.33]
[1,2.33]
При к=3 солнечная шестерня и сателлит имеют одинаковое число зубьев и их определение можно проводить по выражению [1,2.31] или [1,2.33].
Рассмотрим полученную схему 6 ПКП, представленную на рис. 3. Для обеспечения достаточной простоты конструкции ТДМ, входящих в схему ПКП, примем для всех ее четырех рядов одинаковое число сателлитов- d=3. Рассмотри последовательно все четыре планетарных ряда, входящих в схему ПКП.
Для планетарного ряда 7
к7=1.92. Так как![]() , то по выражению [1,2.33],
принимая γ=30, определим число зубьев солнечной шестерни
, то по выражению [1,2.33],
принимая γ=30, определим число зубьев солнечной шестерни

Тогда число зубьев эпицикла
![]()
а число зубьев сателлита
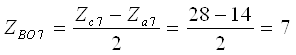
При этом уточненное значение характеристики планетарного ряда
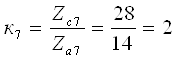
Для планетарного ряда 11
к11=1,9. Так как ![]() , то по выражению [1,2.33], принимая
γ=32, определим число зубьев солнечной шестерни
, то по выражению [1,2.33], принимая
γ=32, определим число зубьев солнечной шестерни
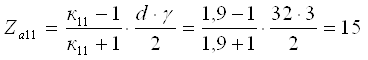
Тогда число зубьев эпицикла
![]()
а число зубьев сателлита
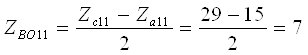
При этом уточненное значение характеристики планетарного ряда
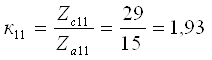
Для планетарного ряда 14
к14=1,5. Так как ![]() , то по выражению [1,2.33],
принимая γ=40, определим число зубьев солнечной шестерни
, то по выражению [1,2.33],
принимая γ=40, определим число зубьев солнечной шестерни
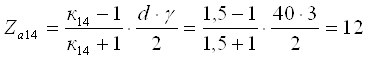
Тогда число зубьев эпицикла
![]()
а число зубьев сателлита
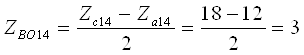
При этом уточненное значение характеристики планетарного ряда

Для планетарного ряда 18
к18=2.17. Так как ![]() , то по выражению [1,2.31],
принимая γ=42, определим число зубьев солнечной шестерни
, то по выражению [1,2.31],
принимая γ=42, определим число зубьев солнечной шестерни
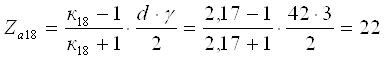
Тогда число зубьев эпицикла
![]()
а число зубьев сателлита
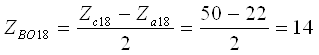
При этом уточненное значение характеристики планетарного ряда
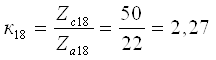
Поскольку при подборе чисел зубьев шестерен планетарных рядов характеристики рядов 7, 11 и 18 изменились незначительно, то следует уточнить значение передаточного числа ПКП для наиболее часто используемой передачи, исключая прямую. В нашем случае мы приняли, что наиболее часто используемой в эксплуатации будет вторая передача.
Тогда для нее, согласно выражению [1,2.28], уточненное значение кинематического передаточного числа
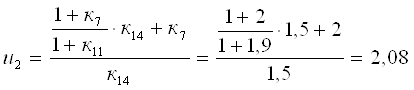
которое отличается от исходного значения u2 = 2 всего на 0,4%.
Примечание: при подборе чисел зубьев шестерен планетарных рядов коробки передач допускается корректировка передаточных чисел до 3%.
В нашем случае передаточное число на наиболее часто используемой передаче изменилось всего на 0,4%, что допустимо. Следовательно, числа зубьев шестерен планетарных рядов подобраны верно.
4. Кинематический анализ планетарной коробки передач
Задачей кинематического анализа является уточнение передаточных чисел ПКП (если при подборе чисел зубьев шестерен планетарных рядов изменялись их характеристики к ) и аналитическое определение абсолютных частот вращения всех центральных звеньев и относительных частот вращения сателлитов на всех передачах.
Кинематический анализ ПКП основан на использовании уравнений кинематики ТДМ.
Рассмотрим схему ПКП (рис. 3) и проанализируем ее работу на всех передачах.
Для этого запишем уравнения кинематики для всех ТДМ, входящих в схему ПКП, в порядке их расположения на схеме:
![]()
![]()
![]()
![]()
Первая передача. Она обеспечивается включением тормоза Т1. Здесь под нагрузкой работают планетарные ряды 7, 11 и 14.
Перепишем уравнения кинематики ТДМ для указанных планетарных рядов:
![]()
![]()
![]()
При включении тормоза Т1 на данной передаче (см. рис. 3) nв7= nв11=0; nа7=nвщ; nа11= nа14=nвм.
![]()
![]()
![]()
Решая уравнения кинематики с учетом уравнений связи, определим передаточное число ПКП:
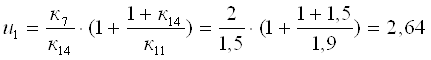
Из схемы ПКП следует, что:
![]()
![]()
![]()
Из уравнения кинематики для планетарного ряда 7, 14 и 18 с учетом уравнений связи определим
![]()
Из уравнения кинематики для планетарного ряда 11, 14 и 18 с учетом уравнений связи определим
![]()
Из уравнения кинематики для планетарного ряда 18 с учетом уравнений связи определим
![]()
Определим относительные частоты вращения всех сателлитов ПКП при включенной первой передаче. Для этого используем выражение [1,2.11]. В результате получим:
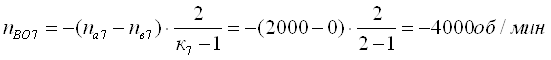
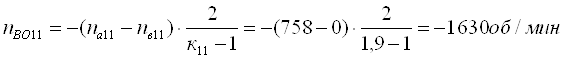

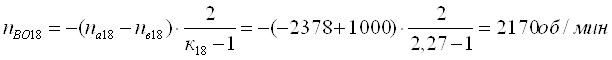
Для оценки возможности использования заданной схемы ПКП необходимо оценить абсолютные частоты вращения всех ее звеньев. Поэтому в табл. 5 заносим результаты выполненных расчетов по абсолютной величине (без учета знаков).
Вторая передача. Обеспечивается включением тормоза Т2 и здесь под нагрузкой работают планетарные ряды 7, 11 и 14.
Передаточное число было определено ранее и его величина
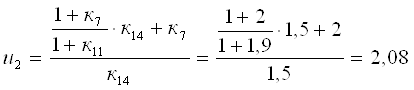
Частоты вращения центральных звеньев ПКП и относительных частот вращения сателлитов на второй передаче определяем аналогично.
Перепишем уравнения кинематики ТДМ для указанных планетарных рядов:
![]()
![]()
![]()
При включении тормоза Т2 на данной передаче (см. рис. 3) nв7= nв11; nа7=nвщ; nа11= nа14=nвм; nс14= nс7= nв18; nв14= nс11= nс18=0.
![]()
![]()
![]()
Из схемы ПКП следует, что:
![]()
![]()
![]()
Из уравнения кинематики для планетарного ряда 7, 14 и 18 с учетом уравнений связи определим
![]()
Из уравнения кинематики для планетарного ряда 11 и 7 с учетом уравнений связи определим
![]()
Из уравнения кинематики для планетарного ряда 18 с учетом уравнений связи определим
![]()
Определим относительные частоты вращения всех сателлитов ПКП при включенной первой передаче. Для этого используем выражение [1,2.11]. В результате получим:
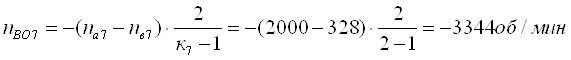
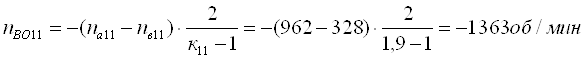
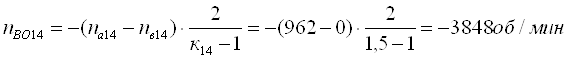
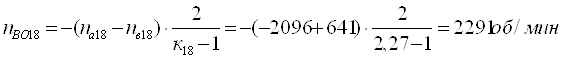
Третья передача. Она обеспечивается включением тормоза Т3. Здесь под нагрузкой работают планетарные ряды 7, 11 и 14.
Перепишем уравнения кинематики ТДМ для указанных планетарных рядов:
![]()
![]()
![]()
При включении тормоза Т3 на данной передаче (см. рис. 3) nв7= nв11; nа7=nвщ; nа11= nа14=nвм; nс14= nс7= nв18=0; nв14= nс11= nс18.
![]()
![]()
![]()
Решая уравнения кинематики с учетом уравнений связи, определим передаточное число ПКП:
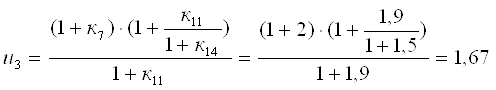
Из схемы ПКП следует, что
![]()
![]()
![]()
Из уравнения кинематики для планетарного ряда 11,14 и 18 с учетом уравнений связи определим
![]()
Из уравнения кинематики для планетарного ряда 11 и 7 с учетом уравнений связи определим
![]()
Из уравнения кинематики для планетарного ряда 18 с учетом уравнений связи определим
![]()
Определим относительные частоты вращения всех сателлитов ПКП при включенной первой передаче. Для этого используем выражение [1,2.11]. В результате получим:
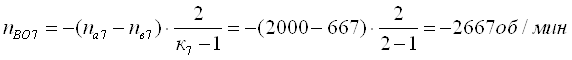
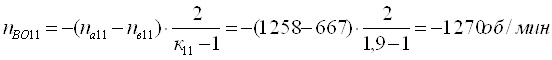
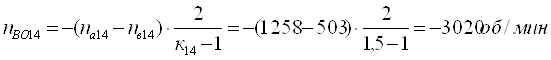
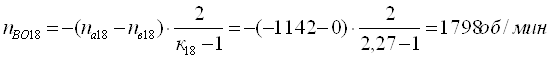
Четвертая передача. Она обеспечивается включением тормоза Т4. Здесь под нагрузкой работают планетарные ряды 7, 11, 14 и 18.
При включении тормоза Т4 на данной передаче (см. рис. 3) nв7= nв11; nа7=nвщ; nа11= nа14=nвм; nс14= nс7= nв18; nв14= nс11= nс18; nа18=0.
![]()
![]()
![]()
![]()
Решая уравнения кинематики с учетом уравнений связи, определим передаточное число ПКП:

Из схемы ПКП следует, что
![]()
![]()
![]()
Из уравнения кинематики для планетарного ряда 7,14 и 18 с учетом уравнений связи определим
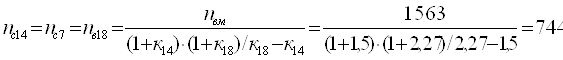
Из уравнения кинематики для планетарного ряда 11,14 и 18 с учетом уравнений связи определим

Из уравнения кинематики для планетарного ряда 11 с учетом уравнений связи определим
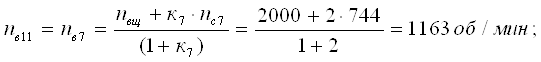
Определим относительные частоты вращения всех сателлитов ПКП при включенной первой передаче. Для этого используем выражение [1,2.11]. В результате получим:
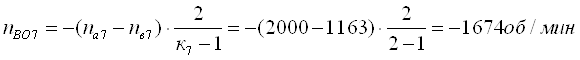
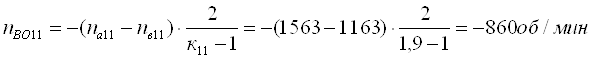
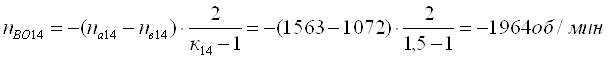
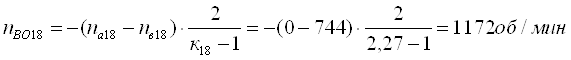
Частоты вращения всех центральных звеньев ПКП и
относительные частоты вращения сателлитов, об/мин
Таблица 5
| Передача | 1 | 2 | 3 | 4 |
| Нагруженные ряды ПКП | 7, 11, 14 | 7, 11, 14 | 7, 11, 14 | 7, 11, 14, 18 |
|
nа7=nвщ |
2000 | 2000 | 2000 | 2000 |
|
nа11= nа14=nвм |
758 | 962 | 1258 | 1563 |
|
nв7= nв11 |
0 | 328 | 667 | 1163 |
|
nс14= nс6= nв18 |
1000 | 641 | 0 | 744 |
|
nв14= nс11= nс18 |
393 | 0 | 503 | 1072 |
|
nа18 |
2378 | 2096 | 1142 | 0 |
|
nВ07 |
4000 | 3344 | 2667 | 1674 |
|
nВ011 |
1630 | 1363 | 1270 | 860 |
|
nВ014 |
4604 | 3848 | 3020 | 1964 |
|
nВ018 |
2170 | 2291 | 1798 | 1172 |
Из анализа частот вращения всех звеньев ПКП видно, что при работе под нагрузкой они не превосходят допустимых пределов.
Таким образом, полученная в результате синтеза схема ПКП обеспечивает работу всех подшипников в области допустимых для них частот вращения.
5. Силовой анализ планетарной коробки передач
Силовой анализ ПКП производится с целью определения максимальных крутящих моментов, нагружающих фрикционные элементы и шестерни планетарных рядов, что необходимо для их последующего расчета.
Крутящие моменты, действующие на звенья планетарного ряда. В ТДМ со смешанным зацеплением шестерен [1, рис. 2.1] абсолютные величины моментов Ма на солнечной шестерне, Мв на водиле и Мс на эпицикле связаны соотношениями:
Мв=Ма(1+к); (2.34)
Мс = Мак; (2.35)
![]() (2.36)
(2.36)
Отметим основные свойства этих соотношений:
1) они справедливы для любого режима работы ТДМ (блокировка, вращение двух звеньев при заторможенном третьем звене, вращение всех звеньев под нагрузкой);
2) если момент одного из звеньев равен нулю, то два других тоже равны нулю и весь ТДМ не нагружен (это свойство используется при определении нагруженных рядов ПКП);
3) зная момент, подведенный к одному звену, можно определить два других момента;
4) совпадающие по направлению моменты солнечной шестерни и эпицикла направлены против момента водила и весь ТДМ уравновешен.
Определение тормозных моментов. Тормозные моменты по отношению к ПКП являются внешними. Кроме тормозного момента при включении передачи с передаточным числом ир≠1 на ПКП действуют еще два внешних момента: на ее ведущем Мвщ и ведомом Мвм валах (рис. 4).
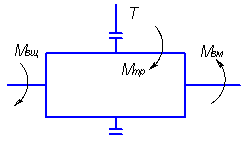
Рис. 4. Схема внешних моментов, действующих на ПКП с двумя степенями свободы
Запишем условие равновесия системы:
![]()
где МТр - момент трения тормоза на р передаче.
Принимая
Мвм=Мвщ uр ηр ,
получим
![]()
Пренебрегая потерями в ПКП (ошибка не превышает 3%), окончательно получим
![]() (2.43)
(2.43)
Выражение [1,2.43] позволяет определить расчетный момент тормоза на любой передаче в ПКП с учетом знака передаточного числа uр.
Определим расчетные моменты на солнечных шестернях всех планетарных рядов выбранной нами ранее схемы ПКП (см. рис. 3), ее тормозов и блокировочного фрикциона. Здесь необходимо рассмотреть работу ПКП на всех передачах.
Первая передача. Под нагрузкой работает планетарные ряды 7, 11 и 14.
Расчетный момент тормоза первой передачи определим по выражению [1,2.43] и уравнениям кинематики и связи для этих рядов.
Тогда
![]()
Момент на солнечной шестерне планетарного ряда 7, 11 и 14
(см. рис. 3)
![]()
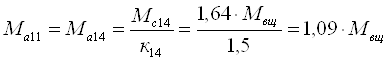
Вторая передача. Под нагрузкой работает планетарные ряды 7, 11 и 14.
Расчетный момент тормоза второй передачи определим по выражению [1,2.43] и уравнениям кинематики и связи для этих рядов.
Тогда
![]()
Момент на солнечной шестерне планетарного ряда 7, 11 и 14
(см. рис. 3)
![]()
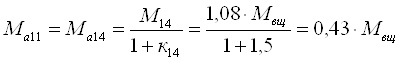
Третья передача. Под нагрузкой работает планетарные ряды 7, 11 и 14.
Расчетный момент тормоза третьей передачи определим по выражению [1,2.43] и уравнениям кинематики и связи для этих рядов.
Тогда
![]()
Момент на солнечной шестерне планетарного ряда 7, 11 и 14
(см. рис. 3)
![]()
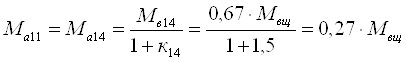
Четвертая передача. Под нагрузкой работает планетарные ряды 7, 11, 14 и 18.
Расчетный момент тормоза четвертой передачи определим по выражению [1,2.43] и уравнениям кинематики и связи для этих рядов.
Тогда
![]()
Момент на солнечной шестерне планетарного ряда 7, 11, 14 и 18
(см. рис. 3)
![]()
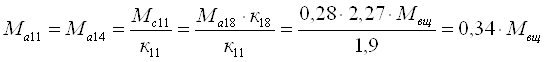
Пятая передача. Включен блокировочный фрикцион Ф и под нагрузкой работают планетарные ряды 7, 11 и 14
![]()
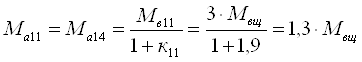
Результаты выполненных расчетов занесены в таблицу 6.
Нагрузки на элементы ПКП
Таблица 6
| Передача |
Расчетный момент в долях от Мвщ |
||||||||
|
МТ1 |
МТ2 |
МТ3 |
МТ4 |
Ф |
Ма7 |
Ма11 |
Ма14 |
Ма18 |
|
| 1 | 1,64 | 0 | 0 | 0 | 0 | 1 | 1,09 | 1,09 | 0 |
| 2 | 0 | 1,08 | 0 | 0 | 0 | 1 | 0,43 | 0,43 | 0 |
| 3 | 0 | 0 | 0,67 | 0 | 0 | 1 | 0,27 | 0,27 | 0 |
| 4 | 0 | 0 | 0 | 0,28 | 0 | 1 | 0,34 | 0,34 | 0,28 |
| 5 | 0 | 0 | 0 | 0 | 3 | 1 | 1,3 | 1,3 | 0 |
Расчеты планетарных рядов коробки передач необходимо выполнять по максимальным нагружающим моментам, величины которых представлены в табл. 6.
Библиографический список
1. Шарипов В. М., Крумбольт Л. Н., Маринкин А. П. Планетарные коробки передач колесных и гусеничных машин./Под общ. ред. В. М. Шарипова.-М.: МГТУ «МАМИ», 2000.-142 с.
2. Проектирование полноприводных колесных машин: В 2 т. Т. 1. Учеб. Для вузов / Б.А. Афанасьев, Н.Ф. Бочаров, Л.Ф. Жеглов; Под ред. А.А. Полунгяна. – М.: Изд-во МГТУ им. Н.Э. Баумана, 1999. – 488 с.
3. Справочник НИИАТ: 12 – е изд. переработанное. и доп. – М.: Транспорт, 1984. – 546 с.
4. Баженов С.П. Методические указания к курсовой работе по теории автомобиля и трактора для очной и очно-заочной формы обучения специальности «Автомобиле- и тракторостроение»/ С.П. Баженов.– Липецк: ЛГТУ, 2001. – 35 с.
5. Конструирование узлов и деталей машин: Учеб. пособие для техн. спец. вузов/ П.Ф. Дунаев, О.П. Леликов. – М.: Высш. шк., 2000. – 447 с.