
Рефераты по рекламе
Рефераты по физике
Рефераты по философии
Рефераты по финансам
Рефераты по химии
Рефераты по хозяйственному праву
Рефераты по экологическому праву
Рефераты по экономико-математическому моделированию
Рефераты по экономической географии
Рефераты по экономической теории
Рефераты по этике
Рефераты по юриспруденции
Рефераты по языковедению
Рефераты по юридическим наукам
Рефераты по истории
Рефераты по компьютерным наукам
Рефераты по медицинским наукам
Рефераты по финансовым наукам
Рефераты по управленческим наукам
Психология педагогика
Промышленность производство
Биология и химия
Языкознание филология
Издательское дело и полиграфия
Рефераты по краеведению и этнографии
Рефераты по религии и мифологии
Рефераты по медицине
Контрольная работа: Сопротивление материалов
Контрольная работа: Сопротивление материалов
УО «Пинский государственный аграрно технический колледж им. А.Е. Клещева
Техническая механика
Контрольная работа
Учащегося(щейся)
КОЛОДКО Александр Николаевич
337 группы
специальности Мелиорация и водное хозяйств
Задача 1
Для ступенчатого
стального бруса требуется: а) определить значения продольной силы и нормального
напряжения по длине бруса; б) построить эпюры ![]() и
и ![]() ; в) определить абсолютное
удлинение (укорочение) бруса. Модуль продольной упругости
; в) определить абсолютное
удлинение (укорочение) бруса. Модуль продольной упругости ![]() МПа.
МПа.
Данные для задачи своего варианта взять из табл. 1 и схемы на рис. 8
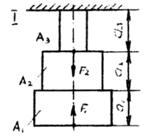
Таблица 1
| Вариант |
|
|
|
|
|
|
|
|
|
||
| кН |
см2 |
см | |||||||||
| 49 | 220 | 100 | 20 | 18 | 12 | 50 | 70 | 80 |
|
||
Решение
1. Определение внутренних усилий.
Разбиваем стержень на участки, проводим сечения и рассматриваем отсеченные участки со свободного конца (рис.1,а).
Согласно определению величина продольной силы численно равна алгебраической сумме проекций всех сил, действующих на оставшуюся часть стержня, на ось стержня.
Участок ![]() ,
, ![]() м:
м:
![]() кН.
кН.
Участок ![]() ,
, ![]() м:
м:
![]() кН.
кН.
Участок ![]() ,
, ![]() м.
м.
![]() кН.
кН.
По полученным данным
строим эпюру продольных сил ![]() (рис.1,б).
(рис.1,б).
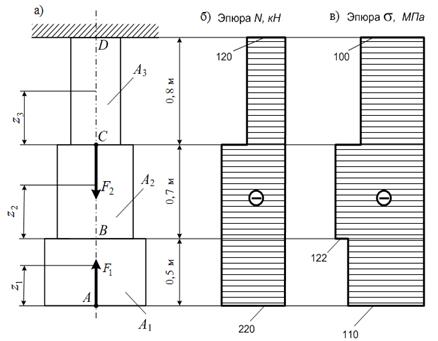
Рис.1. Расчетные схемы к задаче 1
2. Определяем нормальные
напряжения ![]() .
.
Участок ![]() :
:
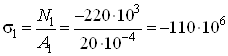 Па
Па![]() МПа.
МПа.
Участок ![]() :
:
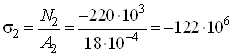 Па
Па![]() МПа.
МПа.
Участок ![]() :
:
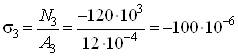 Па
Па![]() МПа.
МПа.
Строим эпюру нормальных
напряжений ![]() (рис.1,в).
(рис.1,в).
3. Определение абсолютного удлинения (укорочения) бруса.
Для определения абсолютного удлинения (укорочения) бруса найдем значения перемещений каждого участка бруса, используя формулу закона Гука.
При этом учтем, что в
точке ![]() (жесткая
заделка) перемещение сечения бруса отсутствует. С этой точки будем отсчитывать
ординаты перемещений.
(жесткая
заделка) перемещение сечения бруса отсутствует. С этой точки будем отсчитывать
ординаты перемещений.
![]() ;
;
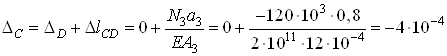 м;
м;
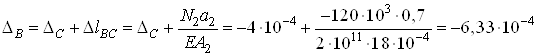 м;
м;
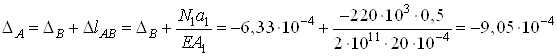 м.
м.
Таким образом, абсолютно брус укоротится на величину
![]() м
м![]() мм.
мм.
Ответ: ![]() мм (брус укоротится).
мм (брус укоротится).
Задача 2
Подобрать сечения
стержней 1 и 2 шарнирно-стержневой конструкции, приняв для растянутых – два
равнополочных, для сжатых – два неравнополочных уголка. Расчет произвести по
предельному состоянию. Расчетное сопротивление ![]() МПа, коэффициент перегрузки
МПа, коэффициент перегрузки ![]() . Коэффициент
условия работы
. Коэффициент
условия работы ![]() .
.
Данные для задачи своего варианта взять из табл. 2 и схемы на рис. 9.
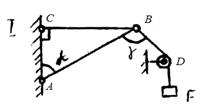
Таблица 2
| Вариант |
|
Углы, град | ||
| кН |
|
|
|
|
| 49 | 90 | 30 | 90 | 110 |
Решение
1. Определение реакций стержней.
В точке ![]() пересекаются линии
действия заданной силы
пересекаются линии
действия заданной силы ![]() реакций стержней
реакций стержней ![]() и
и ![]() , поэтому выделяем узел
, поэтому выделяем узел ![]() (рис.2),
который рассматриваем как объект равновесия. Прикладываем к этому узлу заданную
силу
(рис.2),
который рассматриваем как объект равновесия. Прикладываем к этому узлу заданную
силу ![]() ,
направленную вдоль троса. При этом учитываем, что неподвижный блок
,
направленную вдоль троса. При этом учитываем, что неподвижный блок ![]() изменяет
направление силы, но не влияет на ее значение. Освобождаем узел
изменяет
направление силы, но не влияет на ее значение. Освобождаем узел ![]() от связей, которые
осуществляются стержнями
от связей, которые
осуществляются стержнями ![]() и
и ![]() . Прикладываем вместо них реакции
стержней
. Прикладываем вместо них реакции
стержней ![]() и
и
![]() ,
направляем их вдоль стержня от узла, то есть полагаем, что оба стержня растянуты.
,
направляем их вдоль стержня от узла, то есть полагаем, что оба стержня растянуты.
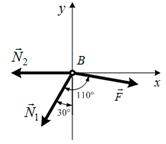
Рис.2. Расчетная схема к задаче 2
Выбираем координатные оси
![]() и
и ![]() , и составляем
уравнения равновесия:
, и составляем
уравнения равновесия:
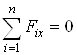 ;
; ![]() ; (1)
; (1)
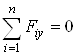 ;
; ![]() ; (2)
; (2)
Решаем уравнения равновесия и находим реакции стержней.
Из уравнения (2) находим
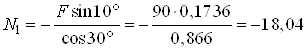 кН.
кН.
Из уравнения (1) получаем
![]() кН.
кН.
Знаки реакций показывают,
что в действительности стержень ![]() сжат, а стержень
сжат, а стержень ![]() растянут.
растянут.
2. Подбор сечений стержней.
При проектировании конструкций условие прочности по первому предельному состоянию записывается в следующем виде:
![]() , (1)
, (1)
где ![]() – наибольшая расчетная
нагрузка в стержне;
– наибольшая расчетная
нагрузка в стержне;
![]() – площадь сечения стержня;
– площадь сечения стержня;
![]() – коэффициент условий работы;
– коэффициент условий работы;
![]() – расчетное сопротивление
материала стержня.
– расчетное сопротивление
материала стержня.
Из условия (1) находим требуемую площадь поперечного сечения стержня
![]() .
.
Для сжатого стержня ![]() будем иметь
будем иметь
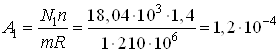 м2
м2![]() см2
см2
По табл. 4 сортамента [1,
с.291], выбираем для заданного сечения стержня два неравнополочных уголка №
2,5/1,6, для каждого из которых площадь профиля ![]() см2. Тогда суммарная
площадь сечения стержня будет
см2. Тогда суммарная
площадь сечения стержня будет ![]() см2
см2![]() см2.
см2.
Для растянутого стержня ![]() получим
получим
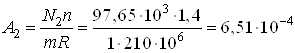 м2
м2![]() см2
см2
По табл. 3 сортамента [1,
с.286] выбираем для сечения стержня два равнополочных уголка № 4 (40´5), для каждого из которых площадь
профиля ![]() см2.
Тогда суммарная площадь сечения второго стержня будет равна
см2.
Тогда суммарная площадь сечения второго стержня будет равна ![]() см2
см2![]() см2.
см2.
Ответ: материал сжатого стержня АВ – два неравнополочных уголка № 2,5/1,6;
материал растянутого стержня ВС – два равнополочных уголка № 4 (40´5).
Задача 3
Найти главные центральные моменты инерции сечения: а) геометрической формы; б) составленного из стандартных профилей проката. Данные для задачи своего варианта взять из табл. 3 и схемы на рис. 10.
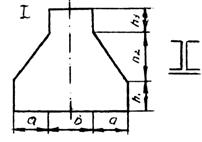
Таблица 3
| Вариант |
|
|
|
|
|
Швеллер, № | Полоса, мм |
| см | |||||||
| 49 | 15 | 40 | 20 | 15 | 20 | 30 |
|
Решение
a) Сечение геометрической формы.
1. Определяем координаты центра тяжести фигуры.
Для этого проводим вспомогательные
оси ![]() ,
, ![]() таким образом,
что ось
таким образом,
что ось ![]() совпадает
с нижним основанием фигуры, а ось
совпадает
с нижним основанием фигуры, а ось ![]() совпадает с ее вертикальной осью
симметрии. Относительно выбранных осей координат определим положение лишь
вертикальной координаты центра тяжести фигуры. Для этого разбиваем сечение на три
прямоугольника I, II и два треугольника III (рис.3).
совпадает с ее вертикальной осью
симметрии. Относительно выбранных осей координат определим положение лишь
вертикальной координаты центра тяжести фигуры. Для этого разбиваем сечение на три
прямоугольника I, II и два треугольника III (рис.3).
Ординату центра тяжести сечения определяем по формуле
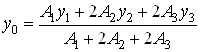 ,
,
где ![]() – площадь прямоугольника
I;
– площадь прямоугольника
I;
![]() см2;
см2;
![]() – расстояние от оси
– расстояние от оси ![]() до центра
тяжести прямоугольника I;
до центра
тяжести прямоугольника I;
![]() см;
см;
![]() – площадь прямоугольника II;
– площадь прямоугольника II;
![]() см2;
см2;
![]() – расстояние от оси
– расстояние от оси ![]() до центра
тяжести прямоугольников II;
до центра
тяжести прямоугольников II;
![]() см;
см;
![]() – площадь треугольника III;
– площадь треугольника III;
![]() см2;
см2;
![]() – расстояние от оси
– расстояние от оси ![]() до центра
тяжести треугольников III;
до центра
тяжести треугольников III;
![]() см;
см;
Подставляя числовые значения, получим
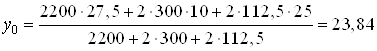 см.
см.
Кроме того, ![]() .
.
По этим данным наносим
точку ![]() –
центр тяжести сечения и проводим главные центральные оси сечения
–
центр тяжести сечения и проводим главные центральные оси сечения ![]() и
и ![]() .
.
2. Вычисляем главные центральные моменты инерции сечения:
![]() ;
; ![]() .
.
Для вычисления момента
инерции прямоугольника I ![]() относительно оси
относительно оси ![]() используем
формулу IV.10 [1, с.82]
используем
формулу IV.10 [1, с.82]
![]() ,
,
где ![]() – момент инерции прямоугольника
относительно собственной центральной оси
– момент инерции прямоугольника
относительно собственной центральной оси ![]() ;
;
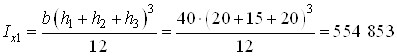 см4;
см4;
![]() – расстояние от оси
– расстояние от оси ![]() до центра
тяжести прямоугольника I
до центра
тяжести прямоугольника I
![]() см.
см.
Подставляя числовые значения, получим
![]() см4.
см4.
Аналогично находим моменты
инерции прямоугольников II и
треугольников III относительно оси ![]() :
:
![]() ,
,
где 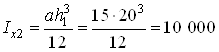 см4;
см4;
![]() см.
см.
![]() см4.
см4.
![]() ;
;
где 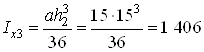 см4;
см4; ![]() см;
см;
![]() см4.
см4.
Суммарный момент инерции
относительно главной оси ![]()
![]() см4.
см4.
Точно также вычисляем
момент инерции относительно главной оси ![]() .
.
Для прямоугольника I
![]() ,
,
где 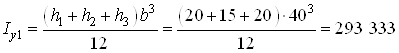 см4;
см4;
![]() см4.
см4.
Для прямоугольника II
![]() ,
,
где 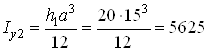 см4;
см4; ![]() см.
см.
![]() см4.
см4.
Для треугольника III
![]() ,
,
где 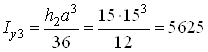 см4;
см4; ![]() см.
см.
![]() см4.
см4.
Суммарный момент инерции
относительно оси ![]()
![]() см4.
см4.
5. Вычерчиваем сечение в масштабе 1:5 с указанием на нем всех осей и размеров (рис.2).
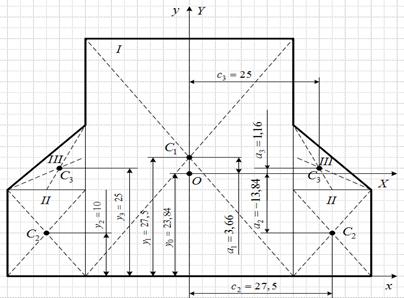
Рис.3. Сечение геометрической формы
a) Сечение, составленное из стандартных профилей проката.
1. Определяем координаты центра тяжести.
Для этого проводим
вспомогательные оси ![]() ,
, ![]() таким образом, что ось
таким образом, что ось ![]() совпадает с нижним
основанием полосы, а ось
совпадает с нижним
основанием полосы, а ось ![]() совпадает с осью симметрии фигуры.
Разбиваем сечение на три фигуры: прямоугольную полосу и два швеллера № 30, для
которых все необходимые данные выбираем из таблиц сортамента [1, c.284].
совпадает с осью симметрии фигуры.
Разбиваем сечение на три фигуры: прямоугольную полосу и два швеллера № 30, для
которых все необходимые данные выбираем из таблиц сортамента [1, c.284].
| Фигура | Размеры, см |
Площадь сечения |
Моменты инерции относительно собственных центральных осей, см4 |
|||
|
|
|
|||||
|
|
|
|||||
| Швеллер № 30 | 30 | 10 | 40,5 | 5810 | 327 | |
Находим геометрические характеристики прямоугольной полосы:
![]() см2;
см2;
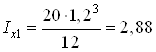 см4;
см4;
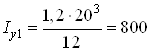 см4.
см4.
Поскольку ось ![]() является осью
симметрии сечения, то она будет являться главной центральной осью сечения
является осью
симметрии сечения, то она будет являться главной центральной осью сечения ![]()
Ординату центра тяжести сечения определяем по формуле
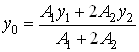 ,
,
где ![]() – расстояние от оси
– расстояние от оси ![]() до центра
тяжести сечения прямоугольной полосы;
до центра
тяжести сечения прямоугольной полосы;
![]() см;
см;
![]() – расстояние от оси
– расстояние от оси ![]() до центра
тяжести швеллеров;
до центра
тяжести швеллеров;
![]() см.
см.
Подставляя числовые значения, получим
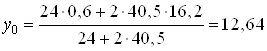 см.
см.
По этим данным наносим
точку ![]() –
центр тяжести сечения и проводим главные центральные оси
–
центр тяжести сечения и проводим главные центральные оси ![]() и
и ![]() .
.
2. Вычисляем главные моменты
инерции относительно осей ![]() и
и ![]() :
:
![]() ;
; ![]() .
.
Вычисляем момент инерции полосы
![]() относительно
оси
относительно
оси ![]()
![]() см4,
см4,
где ![]() – расстояние от оси
– расстояние от оси ![]() до центра
тяжести прямоугольника
до центра
тяжести прямоугольника
![]() см.
см.
Аналогично находим момент
инерции швеллера относительно оси ![]() :
:
![]() ,
,
где ![]() см;
см;
![]() см4.
см4.
Главный момент инерции
![]() см4.
см4.
Точно также вычисляем главный
момент инерции сечения относительно оси ![]() .
.
Для прямоугольной полосы
![]() см4.
см4.
Для швеллера
![]() ,
,
где ![]() см.
см.
![]() см4.
см4.
Суммарный момент инерции
относительно оси ![]()
![]() см4.
см4.
3. Вычерчиваем сечение в масштабе 1:2 с указанием на нем всех осей и размеров (в см) (рис.4).
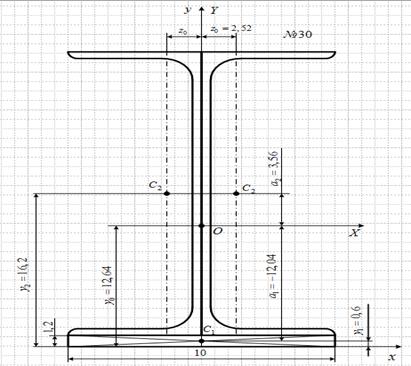
Рис.4. Сечение, составленное из стандартных профилей проката
Задача 4
Построить эпюры поперечных сил и изгибающих моментов от расчетной нагрузки. Проверить несущую способность деревянной балки.
Данные для задачи своего варианта взять из табл. 4 и схемы на рис. 11.
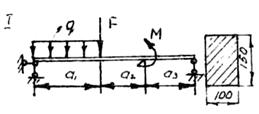
Таблица 4
| Вариант |
|
|
|
|
|
|
| м | ||||||
| 49 | 3 | 6 | 1 | 20 | 12 | 6 |
Решение
1. Выполняем расчетную схему согласно исходных данных (рис.5,а).
Отбросим опоры и заменим
их влияние на балку опорными реакциями ![]() и
и ![]() (рис.5, б).
(рис.5, б).
Определяем опорные реакции.
Составим сумму моментов
всех сил относительно точки ![]() :
:
![]() ;
; 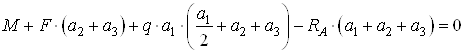 ,
,
откуда
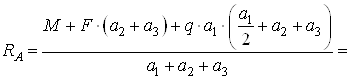
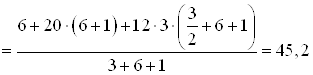 кН.
кН.
Составим сумму моментов
всех сил относительно точки ![]() :
:
![]() ;
; ![]() ,
,
откуда
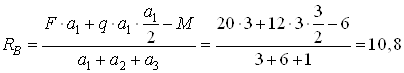 кН.
кН.
Проверка:
![]() .
.
Следовательно, реакции определены правильно.
2. Балка имеет три
участка. Обозначим через ![]() расстояние от левого или правого
концов балки до некоторого его сечения. Составим выражения для поперечных сил
расстояние от левого или правого
концов балки до некоторого его сечения. Составим выражения для поперечных сил ![]() и изгибающих
моментов
и изгибающих
моментов ![]() ,
возникающих в поперечных сечениях балки и по ним установим значения ординат
эпюр в ее характерных сечениях.
,
возникающих в поперечных сечениях балки и по ним установим значения ординат
эпюр в ее характерных сечениях.
Участок I ![]() :
:
![]() ;
;
![]() .
.
При ![]()
![]() кН;
кН;
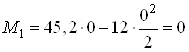 .
.
При ![]() м
м
![]() кН;
кН;
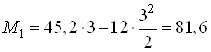 кН∙м.
кН∙м.
Поскольку уравнение
изгибающего момента – уравнение параболы, то для построения эпюры ![]() определим еще
одно значение момента:
определим еще
одно значение момента:
при ![]() м
м
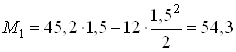 кН∙м.
кН∙м.
Участок II ![]() :
:
![]() ;
;
 .
.
При ![]() м
м
![]() кН;
кН;
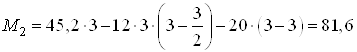 кН∙м.
кН∙м.
При ![]() м
м
![]() кН;
кН;
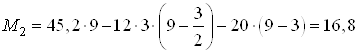 кН∙м.
кН∙м.
Участок III ![]() :
:
![]() ;
;
![]() .
.
При ![]()
![]() кН;
кН;
![]() .
.
При ![]() м
м
![]() кН;
кН;
![]() кН∙м.
кН∙м.
3. По полученным
ординатам строим эпюры ![]() и
и ![]() балки (рис.5, в, г).
балки (рис.5, в, г).
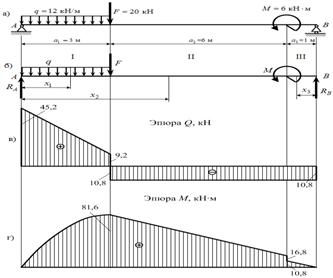
Рис. 5. Расчетные схемы к задаче 4
4. Условие прочности деревянной балки записывается в виде
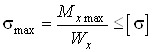 , (1)
, (1)
где ![]() – максимальный
изгибающий момент, действующий в поперечном сечении балки. Из эпюры изгибающих
моментов имеем
– максимальный
изгибающий момент, действующий в поперечном сечении балки. Из эпюры изгибающих
моментов имеем ![]() кН∙м;
кН∙м;
![]() – момент сопротивления сечения
при изгибе; для сечения прямоугольной формы
– момент сопротивления сечения
при изгибе; для сечения прямоугольной формы
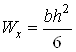 ,
,
где ![]() мм
мм![]() м – ширина прямоугольного
сечения балки;
м – ширина прямоугольного
сечения балки;
![]() мм
мм![]() м – высота прямоугольного сечения
балки;
м – высота прямоугольного сечения
балки;
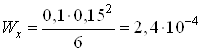 м3;
м3;
![]() – допускаемые напряжения при
изгибе; для дерева принимаем
– допускаемые напряжения при
изгибе; для дерева принимаем ![]() МПа.
МПа.
Проверяем несущую способность деревянной балки
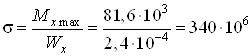 Па
Па![]() МПа,
МПа,
что значительно больше допускаемых напряжений. Следовательно, несущая способность балки не соблюдается.
Ответ: Прочность балки недостаточна.
Задача 5
Для двухопорной балки подобрать сечение двутавра из условия прочности.
Проверить прочность по
касательным напряжениям. Построить эпюры ![]() и
и ![]() для сечений, в которых
для сечений, в которых ![]() и
и ![]() . Нагрузку
принять состоящей: 1) из 80% постоянной, коэффициент перегрузки
. Нагрузку
принять состоящей: 1) из 80% постоянной, коэффициент перегрузки ![]() 2) из 20% временной,
коэффициент перегрузки
2) из 20% временной,
коэффициент перегрузки ![]() .
.
Данные для задачи своего варианта взять из табл. 5 и схемы на рис. 12.
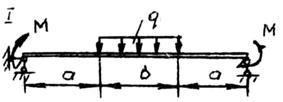
Таблица 5
| Вариант |
|
|
|
|
| м | ||||
| 49 | 4 | 4 | 12 | 6 |
Решение
1. Определяем действительные значения нагрузок, действующих на балку, используя метод расчета предельного состояния по несущей способности.
При этом расчетное усилие
в балке (в нашем случае ![]() и
и ![]() ) определяем как сумму усилий от
каждой нормативной нагрузки (постоянной и временной) с учетом соответствующих
каждой нагрузке коэффициентов перегрузки. В результате получим
) определяем как сумму усилий от
каждой нормативной нагрузки (постоянной и временной) с учетом соответствующих
каждой нагрузке коэффициентов перегрузки. В результате получим
![]() кН∙м;
кН∙м;
![]() кН/м.
кН/м.
2. Выполняем расчетную схему согласно исходных данных (рис.6,а).
Отбросим опоры и заменим
их влияние на балку опорными реакциями ![]() и
и ![]() (рис.6, б). Учитывая
симметричность конструкции, получим
(рис.6, б). Учитывая
симметричность конструкции, получим
![]() кН.
кН.
2. Балка имеет три
участка. Обозначим через ![]() расстояние от левого или правого
концов балки до некоторого его сечения. Составим выражения для поперечных сил
расстояние от левого или правого
концов балки до некоторого его сечения. Составим выражения для поперечных сил ![]() и изгибающих
моментов
и изгибающих
моментов ![]() ,
возникающих в поперечных сечениях балки и по ним установим значения ординат
эпюр в ее характерных сечениях.
,
возникающих в поперечных сечениях балки и по ним установим значения ординат
эпюр в ее характерных сечениях.
Участок I ![]() :
:
![]() ;
;
![]() .
.
При ![]()
![]() кН;
кН;
![]() кН∙м.
кН∙м.
При ![]() м
м
![]() кН;
кН;
![]() кН∙м.
кН∙м.
Участок II ![]() :
:
![]() ;
;
 .
.
При ![]() м
м
![]() кН;
кН;
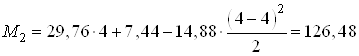 кН∙м.
кН∙м.
При ![]() м
м
![]() кН;
кН;
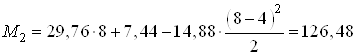 кН∙м.
кН∙м.
Так как на концах участка II поперечная сила меняет свой знак с плюса на минус, то на данном участке изгибающий момент принимает максимальное значение.
Из условия ![]() найдем абсциссу
найдем абсциссу ![]() сечения, в
котором действует изгибающий момент
сечения, в
котором действует изгибающий момент ![]() :
:
![]() ,
,
откуда
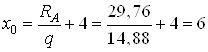 м.
м.
Тогда при ![]() м
м
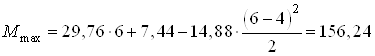 кН∙м.
кН∙м.
Участок III ![]() :
:
![]() ;
;
![]() .
.
При ![]()
![]() кН;
кН;
![]() .
.
При ![]() м
м
![]() кН;
кН;
![]() кН∙м.
кН∙м.
3. По полученным
ординатам строим эпюры ![]() и
и ![]() балки (рис.6, в, г).
балки (рис.6, в, г).
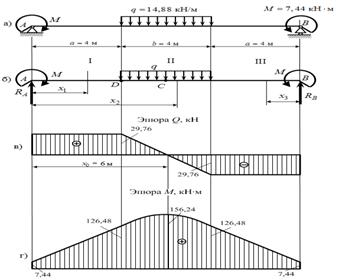
Рис. 3. Расчетные схемы к задаче 3
4. Определяем из условия прочности необходимый момент сопротивления сечения
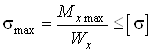 , (1)
, (1)
где ![]() – максимальный
изгибающий момент, действующий в поперечном сечении балки. Из эпюры изгибающих
моментов имеем
– максимальный
изгибающий момент, действующий в поперечном сечении балки. Из эпюры изгибающих
моментов имеем ![]() кН∙м;
кН∙м;
![]() – момент сопротивления сечения
при изгибе;
– момент сопротивления сечения
при изгибе;
![]() – допускаемые напряжения при
изгибе; принимаем для стали Ст3
– допускаемые напряжения при
изгибе; принимаем для стали Ст3
![]() МПа.
МПа.
Из выражения (1) находим требуемый момент сопротивления сечения
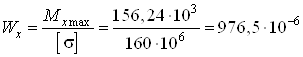 м3
м3![]() см3.
см3.
Для подбора сечения балки
в виде двутавра используем таблицу сортамента [1, с.283], откуда выбираем для
заданного сечения балки двутавр № 40, для которого ![]() см3. Перегрузка при
этом составит
см3. Перегрузка при
этом составит
![]() ,
,
что вполне допустимо (< 3%).
5. Построим эпюры ![]() и
и ![]() для сечений, в
которых
для сечений, в
которых ![]() и
и
![]() .
.
Сечение С (расположено посередине пролета ![]() ). В данном
сечении действуют только нормальные напряжения, так как поперечная сила равна
нулю.
). В данном
сечении действуют только нормальные напряжения, так как поперечная сила равна
нулю.
Нормальные напряжения вычисляем по формуле Навье
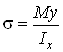 .
.
В данном сечении ![]() кН∙м,
кН∙м, ![]() кН.
кН.
Данные для двутавра №40: ![]() мм;
мм; ![]() мм;
мм; ![]() мм;
мм; ![]() мм;
мм; ![]() см2;
см2;
![]() см4;
см4;
![]() см3.
см3.
Обозначим характерные точки по высоте сечения (рис.7).
Точка 1:
![]() мм
мм![]() м;
м;
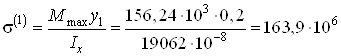 Па
Па![]() МПа.
МПа.
Поскольку изгибающий момент положительный, то точки 1 и 2 лежат в сжатой зоне и напряжения в этих точках имеют отрицательный знак.
Точка 2:
![]() мм
мм![]() м;
м;
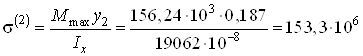 Па
Па![]() МПа.
МПа.
Точка 3:
![]() , так как
, так как ![]() . Ось, проходящая через точку 3,
называется нейтральной осью.
. Ось, проходящая через точку 3,
называется нейтральной осью.
Точки 4 и 5. В этих точках значения нормальных напряжений те же, что и в точках 2 и 1, только положительные, так как точки 4 и 5 лежат в растянутой зоне.
![]() МПа;
МПа;
![]() МПа.
МПа.
По полученным значениям
строим эпюру ![]() (рис.7).
(рис.7).
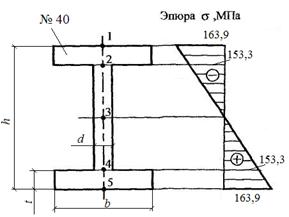
Рис.7. Эпюра нормальных напряжений в сечении С
Сечение D. Здесь действует максимальная
поперечная сила ![]() кН, а изгибающий момент равен
кН, а изгибающий момент равен ![]() кН∙м.
кН∙м.
Касательные напряжения ![]() вычисляем по
формуле
вычисляем по
формуле
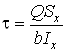 .
.
В точках 1 и 5 ![]() (рис.8).
(рис.8).
Точки 2 и 4. Вычисляем статический момент площади поперечного сечения
![]() ,
,
где ![]() – отсеченная часть
площади поперечного сечения;
– отсеченная часть
площади поперечного сечения;
![]() – координата центра тяжести
отсеченной площади.
– координата центра тяжести
отсеченной площади.
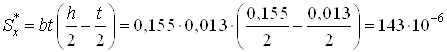 м3.
м3.
При ![]() мм
мм
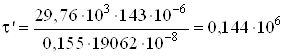 Па
Па![]() МПа.
МПа.
При ![]() мм
мм
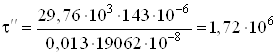 Па
Па![]() МПа.
МПа.
Точка 3. Это точка, расположенная на уровне нейтральной оси. Для нее имеем [2, с.257]
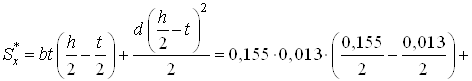
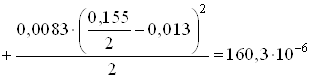 м3.
м3.
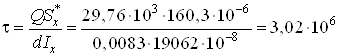 Па
Па![]() МПа.
МПа.
Нормальные напряжения в сечении D
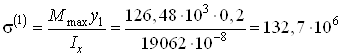 Па
Па![]() МПа (сжатие);
МПа (сжатие);
![]() МПа (растяжение).
МПа (растяжение).
Строим эпюры напряжений в сечении D (рис.8).
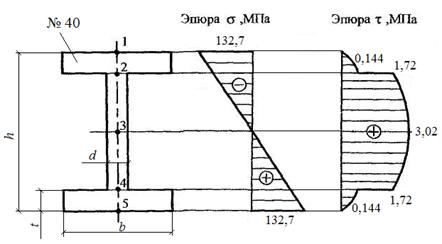
Рис. 8. Эпюра касательных напряжений в сечении А
Максимальное касательное
напряжение имеет место на нейтральной линии, то есть ![]() МПа.
МПа.
Допускаемое касательное
напряжение по 3-й теории прочности принимаем равным ![]() МПа.
МПа.
Следовательно, для балки двутаврового сечения
![]() МПа<96МПа
МПа<96МПа![]() .
.
Условие прочности выполняется.
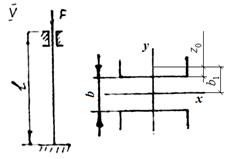
Задача 6
Подобрать сечение
равноустойчивой центрально сжатой колонны из двух швеллеров или двутавров (в
зависимости от варианта выполняемой задачи), соединенных планками способом
сварки. Материал - сталь Ст3, расчетное сопротивление ![]() МПа. Данные для задачи своего
варианта взять из табл. 7 и рис. 13. Принять
МПа. Данные для задачи своего
варианта взять из табл. 7 и рис. 13. Принять ![]() .
.
| Вариант | Схема на рис. |
|
|
|
|
|
|
|
% от |
|||||||
| 49 | V | 6 | 0,6 | 30 | 70 | 1,3 | 1 |
Решение
1. Определяем действительное значение нагрузки, действующей на колонну, используя метод расчета предельного состояния по несущей способности.
При этом расчетное усилие
в колонне (в нашем случае ![]() ) определяем как сумму усилий от
каждой нормативной нагрузки (постоянной и временной) с учетом соответствующих
данной нагрузке коэффициентов перегрузки. В результате получим
) определяем как сумму усилий от
каждой нормативной нагрузки (постоянной и временной) с учетом соответствующих
данной нагрузке коэффициентов перегрузки. В результате получим
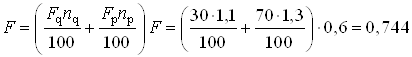 МН
МН![]() кН.
кН.
2. Равноустойчивость
колонны во всех направлениях будет обеспечена при равенстве моментов инерции
относительно осей ![]() и
и ![]() . Момент инерции сечения
относительно оси
. Момент инерции сечения
относительно оси ![]() не зависит от расстояния
не зависит от расстояния ![]() , поэтому
подбор сечения произведем, учитывая это обстоятельство.
, поэтому
подбор сечения произведем, учитывая это обстоятельство.
3. Принимая в качестве
первого приближения значение коэффициента ![]() , находим площадь поперечного
сечения колонны
, находим площадь поперечного
сечения колонны
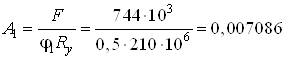 м2
м2![]() см2.
см2.
Из таблиц сортамента [1,
с.284] выбираем два швеллера № 30, для которых суммарная площадь сечения равна ![]() см2.
см2.
Наименьший радиус инерции из той же таблицы для составного сечения
![]() см.
см.
Определяем гибкость колонны
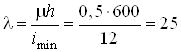 .
.
Коэффициент ![]() из табл.X.1[1] получаем равным
из табл.X.1[1] получаем равным ![]() .
.
Повторим расчет, принимая
![]() .
.
Далее находим
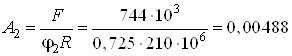 м2
м2![]() см2.
см2.
Из таблиц сортамента [1,
с.284] выбираем два швеллера № 20а, для которых суммарная площадь сечения равна
![]() см2;
см2;
![]() см.
Гибкость колонны при этом будет равна
см.
Гибкость колонны при этом будет равна
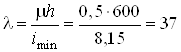 .
.
Коэффициент ![]() из табл.X.1 получаем равным
из табл.X.1 получаем равным ![]() .
.
Еще раз повторим расчет, приняв
![]() .
.
Далее получаем
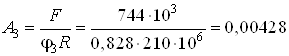 м2
м2![]() см2.
см2.
Выбираем швеллер № 18а.
Тогда ![]() см2;
см2;
![]() см.
см.
Гибкость
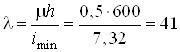 .
.
Коэффициент продольного
изгиба при этом равен ![]() .
.
Еще раз произведем расчет
![]() .
.
Далее получаем
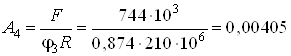 м2
м2![]() см2.
см2.
Выбираем швеллер № 18.
Тогда ![]() см2;
см2;
![]() см.
см.
Гибкость
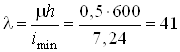 .
.
Коэффициент продольного
изгиба при этом равен ![]() и очень мало отличается от
и очень мало отличается от ![]() . Расчет
заканчиваем и принимаем швеллер № 18, для которого
. Расчет
заканчиваем и принимаем швеллер № 18, для которого ![]() см4;
см4; ![]() см4;
см4; ![]() см2.
см2.
Момент инерции сечения
колонны относительно оси ![]() равно
равно
![]() см4.
см4.
Момент инерции сечения
колонны относительно оси ![]() равно
равно
![]() .
.
Условие равноустойчивости имеет вид
![]() .
.
Подставляя сюда значения моментов инерции, получим
![]() ,
,
откуда находим расстояние
от центра тяжести швеллера до оси ![]()
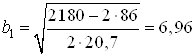 см.
см.
Определяем длину пластин
![]() см
см
Ответ: Сечение колонны: два швеллера № 18,
соединенные пластинами длиной ![]() см способом сварки.
см способом сварки.
Список использованной литературы
1. Степин П.А. Сопротивление материалов. М.: Высшая школа, 1983.
2. Дарков А.В., Шпиро Г.С. Сопротивление материалов. М.: Высшая школа, 1989.
3. Ицкович Г.М. Сопротивление материалов. М.: Высшая школа, 1986.