
Рефераты по рекламе
Рефераты по физике
Рефераты по философии
Рефераты по финансам
Рефераты по химии
Рефераты по хозяйственному праву
Рефераты по экологическому праву
Рефераты по экономико-математическому моделированию
Рефераты по экономической географии
Рефераты по экономической теории
Рефераты по этике
Рефераты по юриспруденции
Рефераты по языковедению
Рефераты по юридическим наукам
Рефераты по истории
Рефераты по компьютерным наукам
Рефераты по медицинским наукам
Рефераты по финансовым наукам
Рефераты по управленческим наукам
Психология педагогика
Промышленность производство
Биология и химия
Языкознание филология
Издательское дело и полиграфия
Рефераты по краеведению и этнографии
Рефераты по религии и мифологии
Рефераты по медицине
Контрольная работа: Шарнирно-рычажные и кулачковые механизмы
Контрольная работа: Шарнирно-рычажные и кулачковые механизмы
Шарнирно-рычажные механизмы, классификация звеньев по виду движения. Кулачковые механизмы, принцип действия, наименование звеньев. Область применения
В шарнирно-рычажных механизмах жесткие звенья типа стержней, рычагов соединяются вращательными и поступательными кинематическими парами. Шарнирно-рычажные механизмы применяются для преобразования вращательных или поступательных движений входных звеньев в качательное или возвратно-поступательное движение выходных звеньях.
В зависимости от характера движения и назначения звенья имеют определенные названия. Звено, совершающее полный оборот вокруг неподвижной оси - кривошип; плоскопараллельное движение имеет шатун; качательное - коромысло; поступательное - ползун; направляющая - неподвижное звено, образующее поступательную пару с ползуном; коромысло, служащее направляющей для ползуна (кулисного камня) - кулиса и др.
Кулачковые механизмы - механизмы с высшими кинематическими парами, которые образуются путем силового и геометрического замыкания его звеньев: кулачка и толкателя; кулачка и коромысла. Эти механизмы используются для преобразования вращательного движения входного звена в возвратно-поступательное, качательное или сложное движение выходного с остановками заданной продолжительности.
Кулачковые механизмы в зависимости от движения выходного звена делятся на три вида:
1. Выходное звено движется поступательно.
2. Выходное звено вращается.
3. Выходное звено совершает сложное движение.
Цилиндр, ограниченный в сечении плоской кривой, вращается вокруг оси с заданной угловой скоростью. Действуя на ролик, свободно вращающийся вокруг оси, цилиндр заставляет второе звено совершать одно из перечисленных выше движений.
Кулачком называется звено высшей пары, элемент которого имеет переменную кривизну. Если выходное звено движется поступательно, оно называется толкателем; если вращается, то коромыслом; а если совершает сложное движение, то называется шатуном.
Кулачковые механизмы находят широкое применение в специальном технологическом оборудовании электронной промышленности. Кулачковый механизм применяется в двигателях внутреннего сгорания в газораспределительном механизме, в металлорежущих станках и других машинах для воспроизведения сложной траектории движения рабочих органов и выполнения функций управления, таких как включение и выключение рабочих органов по определённой схеме.
Многозвенные механические передачи: многоступенчатые передачи, ряд последовательно зацепляющихся колес. Определение передаточного отношения каждого из указанных видов механизма, изобразите кинематические схемы.
Для осуществления значительных передаточных отношений применяются несколько последовательно соединенных колес, где, кроме входного и выходного имеются еще промежуточные колеса, такие передачи называются многоступенчатыми.
Многоступенчатые передачи, у которых оси вращения колес неподвижны, носят также названия рядового соединения.
Передаточное отношение сложной многоступенчатой зубчатой передачи есть произведение взятых со своими знаками передаточных отношений отдельных его ступеней.
U1n = ω1/ωn = U12·U2’3·U3’4·…·U (n-1) ’n
Для каждой ступени передач имеем:
U12 = ± (r2/r1) = ± (z2/z1),
U2’3 = ± (r3/r2’) = ± (z3/z2’),
………………………….
U (n-1) ’n = ± (rn/r (n-1) ’) = ± (zn/z (n-1) ’),
где r1, r2, r2’, r3,…., r (n-1) ’, rn - радиусы начальных окружностей колес, а
z1, z2, z2’, z3,…., z (n-1) ’, zn - числа зубьев, причем верхний знак берется при внутреннем, а нижний - при внешнем зацеплении.
В инженерных расчетах также пользуются формулой:
U1n = ω1/ωn = (-1) m ∙U12·U2’3·U3’4·…·U (n-1) ’n,
где m - число внешних зацеплений.
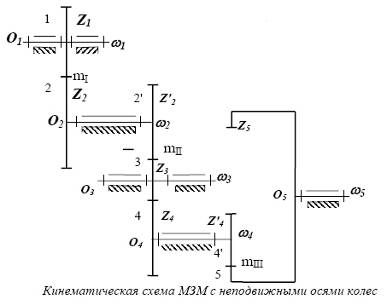
В некоторых многоступенчатых зубчатых передачах оси отдельных колес являются подвижными. Такие зубчатые механизмы с одной степенью свободы называются планетарными механизмами, а с двумя и более степенями свободы дифференциальными механизмами или просто дифференциалами. В этих механизмах колеса с подвижными осями вращения называются планетарными колесами или сателлитами, а звено, на котором располагаются оси сателлитов - водилом. На схемах водило принято обозначать буквой Н. Зубчатые колеса с неподвижными осями вращения называются солнечными или центральными; неподвижное колесо - опорным.
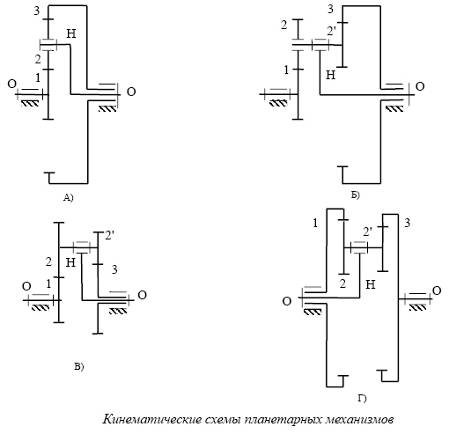
Передаточное отношение определяется по формуле Виллиса:
![]()
Формула Виллиса читается так: передаточное отношение от колеса с номером К к водилу Н при неподвижном колесе с номером L равно единице минус передаточное отношение от колеса с номером К к открепленному колесу с номером L при закрепленном водиле Н. Заметим, что планетарный механизм с закрепленным (условно) водилом Н превращается в многозвенный механизм с неподвижными осями колес. Обычно закрепленное звено обозначается в выражении передаточного отношения верхним индексом в скобках. Пусть у редуктора Давида (тип В) ведущим является колесо 1, неподвижным колесо 3, тогда:
![]()
Для всех типов механизмов изображенных на рисунке, выражения передаточных отношений могут быть сведены в таблицу 1.
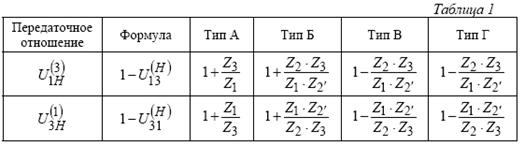
Во многих планетарных механизмах ведущим может быть водило Н.
Тогда передаточное отношение ![]() определяется, как обратное выражению
определяется, как обратное выражению
![]() :
:
![]()
Формулу Виллиса можно обобщить на дифференциал с любым числом колес до k:
![]()
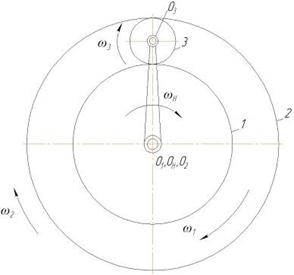
Схема зубчатого дифференциального механизма с цилиндрическими колесами.
Трение в винтовой паре. Трение в цапфах и пятах
При рассмотрении трения в винтовой кинематической паре обычно делают целый ряд допущений. Во-первых, так как закон распределения давлений по винтовой резьбе неизвестен, то условно считают, что сила давления гайки на винт или, наоборот, винта на гайку приложена по средней линии резьбы. Средняя линия резьбы расположена на расстоянии r от оси винта. Во-вторых, предполагается, что действие сил в винтовой паре может быть сведено к действию сил на ползун, находящийся на наклонной плоскости. Развертывая среднюю линию винтовой резьбы на плоскость, сводят пространственную задачу к плоской.
Тогда сила трения:
![]()
f = tgφ - коэффициент трения,
β - угол подъема винтовой резьбы,
F - сила, необходимая для равномерного перемещения гайки.
Этим соотношением можно пользоваться при определении сил трения в винтовых парах с прямоугольной резьбой. При треугольной резьбе весьма приближенно считают, что движение гайки аналогично движению клинового ползуна по желобу, у которого угол между вертикалью и стенками желоба равен 90°-α, где α - угол подъема резьбы. Сила трения:
![]()
![]()
Так как коэффициент трения f’ больше коэффициента трения f, то трение в винтовой паре с треугольной резьбой больше, чем в винтовой паре с резьбой прямоугольной.
При рассмотрении трения в цапфах предполагают, что вал, располагающийся в подшипнике, находится под действием радиальной силы F’ и внешнего момента М и вращается с постоянной угловой скоростью ω. Между валом и подшипником имеется радиальный зазор. Тогда при вращении вала, при наличии трения между валом и подшипником его цапфа будет как бы "взбегать" на подшипник. Предположим, что вследствие "взбегания" цапфы на подшипник касание элементов кинематической пары оказывается в точке, где реакция F’’ параллельна силе F’. На основании ранее установленных положений полная реакция F’’ должна быть отклонена от нормали на угол трения φ, и величина силы трения FТ получается равной:
![]() ,
,
так как при равновесии цапфы F’’= F’.
Момент М, приложенный к цапфе, уравновешивается моментом трения МТ, равным:
МТ = Fr = fF’rcosφ = F’rsinφ = F’ρ
Если из центра вала О описать радиусом ρ окружность, то полная реакция F’’ будет направлена по касательной к этой окружности. Круг радиуса ρ называется кругом трения. Так как углы трения малы, то можно считать:
sinφ ≈ tgφ,
ρ ≈ rf.
Момент трения:
МТ = F’rf’,
где r - радиус цилиндрического элемента пары, f’ - коэффициент трения во вращательной паре, F’ - результирующая нагрузка на цапфу.
В некоторых случаях вращательные пары выполняют в виде пяты и подпятника, нагруженных осевой силой F. В этом случае на поверхности касания пяты и подпятника возникает сила трения верчения, починяющаяся закону Амонтона-Кулона.
Если пята кольцевая, то момент трения:
![]()
Если пята не кольцевая, а сплошная:
![]()
Расчет ненапряженных и напряженных болтовых соединений. Расчет эксцентрично нагруженных болтов. Сравните степень нагруженности болтовых соединений различных типов.
Стержень винта нагружен только внешней растягивающей силой. Примером служит резьбовой участок крюка для подвешивания груза. Опасным является сечение, ослабленное резьбой. Площадь этого сечения оценивают приближенно по внутреннему диаметру d1 резьбы. Условие прочности:
σ = F/ [ (π/4) d12] ≤ [σ].
Болт затянут, внешняя нагрузка отсутствует. Примером служат болты для крепления ненагруженных герметичных крышек и люков корпусов машин. В этом случае стержень болта растягивается осевой силой Fзат, возникающей от затяжки болта, и закручивается моментом сил трения в резьбе Тр. Напряжение растяжения от силы Fзат:
σ = Fзат/ [ (π/4) d12].
Напряжение кручения от момента Тр:
τ = Тр/Wp = 0,5Fзатd2tg (ψ+φ) / (0,2d13).
Требуемое значение от силы затяжки:
Fзат = Аσсм,
где А - площадь стыка деталей, приходящаяся на один болт,
σсм - напряжение смятия в стыке деталей.
Прочность болта определяют по эквивалентному напряжению:
![]() .
.
Для стандартных метрических резьб:
σэк ≈1,3 σ.
Это позволяет рассчитывать прочность болтов по упрощенной формуле:
σэк = 1,3Fзат/ [ (π/4) d12] ≤ [σ].
Болтовое соединение нагружено силами, сдвигающими детали в стыке. Условием надежности соединения является отсутствие сдвига деталей в стыке. Может быть два варианта.
Первый вариант - болт поставлен с зазором. Пи этом внешнюю нагрузку F уравновешивают силами трения в стыке, которые образуются от затяжки болта.
Fзат = КF/ (if),
где i - число плоскостей стыка деталей, f - коэффициент трения в стыке, К - коэффициент запаса. Прочность болта оценивают по эквивалентному напряжению:
σэк = 1,3Fзат/ [ (π/4) d12] ≤ [σ].
Второй вариант - болт поставлен без зазора. При расчете прочности соединения не учитывают силы трения в стыке, так как затяжка болта не обязательна. Стержень болта рассчитывают по напряжениям среза и смятия. Условие прочности по напряжениям среза:
τ = F/ [ (π/4) d2i] ≤ [τ].
Для средней детали в соединении:
σсм = F/ (dδ2) ≤ [σсм].
Для крайней детали в соединении:
σсм = F/ (2dδ1) ≤ [σсм].
Эти формулы справедливы для болта и для деталей. Из двух значений σсм в этих формулах расчет прочности выполняют по наибольшему, а допускаемое напряжение определяют по более слабому материалу болта или детали.
Сравнивая варианты установки болтов с зазором и без зазора, следует отметить, что первый вариант дешевле второго. Однако условия работы болта, поставленного с зазором, хуже, чем без зазора. Кроме того, вследствие нестабильности коэффициента трения и трудности контроля затяжки работа таких соединений при сдвигающей нагрузке недостаточно надежна.
Болт затянут, внешняя нагрузка раскрывает стык деталей. Примером служат болты для крепления крышек резервуаров, нагруженных давлением р жидкости или газа. Затяжка болтов должна обеспечивать герметичность соединения или нераскрытие стыка под нагрузкой.
Расчетная нагрузка болта:
Fp = Fзат + χF,
где χ - коэффициент внешней нагрузки.
Остаточная затяжка стыка от одного болта:
Fст = Fзат - (1 - χ) F.
При статических нагрузках прочность болта в соединении оценивают по формуле:
σ = 1,3Fр/ [ (π/4) d12] ≤ [σ].
При переменных нагрузках полное напряжение в болте можно разделить на постоянное:
σm = [Fзат + (Fб/2)] /Aб
и переменное с амплитудой:
σа = (Fб/2) /Aб
Запас статической прочности по текучести материала определяют по формуле:
sT = σT/ σmax = σT/ (σm + σa).
Экцентричное нагружение болта возникает из-за непараллельности опорных поверхностей детали и гайки или головки болта.
В этих случаях кроме напряжений растяжения в стержне болта появляются напряжения изгиба.
Напряжение растяжения в стержне:
σр = Fзат/ [ (π/4) d12].
Напряжения изгиба при больших значениях угла наклона опорной поверхности, не ограничивающих деформацию болта:
σи = Fзат χ/ (0,1d13).
При малых значениях угла наклона опорной поверхности напряжения изгиба определяют с учетом деформации, допускаемой этим углом:
σи = М/Wи ≈ Еda/ (2lб).
Расчетным напряжением σи будет меньшее из двух. Экцентричное нагружение значительно уменьшает прочность болтов.
Наиболее тяжелые условия работы для болта вызывает экцентричное нагружение болтов. Для болта предпочтительнее нагружение растягивающей силой, чем работа на срез. Сравнение установки болтов с зазором и без зазора приведено выше.
Червячная передача. Основные геометрические и кинематические соотношения. Передаточное отношение. Самотормозящаяся червячная передача. КПД червячной передачи. Материалы элементов червячных передач. Достоинства и недостатки червячных передач, область их применения. Приведите известные вам примеры из вашей практики применения червячной передачи. Какие эксплуатационные свойства вами наблюдались в процессе эксплуатации?
Червячная передача относится к передачам зацепления с перекрещивающимися осями валов. Угол перекрещивания обычно равен 90°. Движение в червячных передачах преобразуется по принципу винтовой пары или по принципу наклонной плоскости.
Делительные диаметры червяка и колеса:
d1 = qm, d2 = z2m.
Диаметры выступов:
da1 = d1 + 2m, da2 = d2 + 2m.
Диаметры впадин:
df1 = d1 - 2,4m, df2 = d2 - 2,4m.
Межосевое расстояние:
aW = 0,5 (q + z2) m.
m - модуль. q - коэффициент диаметра червяка. Угол подъема винтовой линии γ:
tgγ = πmz1/ (πd1) = mz1/d1 = z1/q.
Червячные передачи со смещением.
Межосевое расстояние:
aW = 0,5 (q + z2 + 2х) m.
У червячного колеса со смещением:
da2 = (z2 + 2 + 2x) m, df2 = (z2 - 2,4 + 2x) m.
Передаточное отношение:
i = n1/n2 = z2/z1
z1 - число заходов червяка.
Так как z1 может быть небольшим и часто равным единице, то в одной червячной паре можно получить большое передаточное отношение. Это и является основным достоинством червячных передач.
При движении витки червяка скользят по зубьям колеса, как в винтовой паре. Большое скольжение в червячных передачах служит причиной пониженного КПД, повышенного износа и склонности к заеданию, что является основными недостатками червячных передач.
КПД зацепления при ведущем червяке:
ηз = tgγ/tg (γ + φ)
КПД увеличивается с увеличением числа заходов червяка и с уменьшением коэффициента трения или угла трения φ.
Если ведущим является колесо, то вследствие изменения направления сил получают:
ηз = tg (γ - φ) / tgγ.
При γ ≤ φ, ηз = 0 передача движения в обратном направлении (от колеса к червяку) становится невозможной. Получаем самотормозящую червячную пару. Свойство самоторможения червячных передач используют в грузоподъемных и других механизмах.
шарнирный рычажный кулачковый механизм
Основные преимущества червячной передачи: возможность получения больших передаточных отношений; плавность и бесшумность в работе; повышенная кинематическая точность; возможность самоторможения. Недостатки: сравнительно низкий КПД; повышенный износ и склонность к заеданию; необходимость применения для колес дорогих антифрикционных материалов (бронза); повышенные требования к точности сборки. Червячные передачи применяют при необходимости передачи движения между перекрещивающимися валами, а также в механизмах, где необходимы большие передаточные отношения и высокая кинематическая точность, например делительные устройства, механизмы наведения. Эти передачи применяют в подъемно-транспортных машинах, станкостроении, автомобилестроении.
Червяки современных передач изготовляют из углеродистых или легированных сталей (сталь 45, сталь 40Х и др.). Наибольшей нагрузочной способностью обладают пары, у которых витки червяка подвергают термообработке до высокой твердости (закалка, цементация) с последующим шлифованием.
Червячные колеса изготовляют преимущественно из бронзы, реже из латуни или чугуна. Оловянные бронзы типа О10Ф1, О10Н1Ф1 и другие считаются лучшим материалом для червячных колес. Безоловянные бронзы, например А9Ж4 обладают повышенными механическими характеристиками, но имеют пониженные противозадирные свойства.
Из практики: применение червячного редуктора в подъемнике. Свойство самоторможения червячных передач.
Критерии работоспособности, виды разрушения подшипников качения. Методика подбора и проверочного расчета подшипников качения. Какие виды разрушения элементов подшипников качения наблюдали вы лично? В чем причина?
Условия работы подшипника качения, влияющие на его работоспособность. Распределение нагрузки между телами качения в значительной степени зависит от размера зазора в подшипнике и точности геометрической формы его деталей. Зазоры увеличиваются от износа подшипника в эксплуатации. Контактные напряжения в деталях подшипников. С переменными контактными напряжениями связан усталостный характер разрушения рабочих поверхностей деталей подшипников (выкрашивание). Кинематика подшипника. Угловая скорость сепаратора зависит от размеров шарика. При неточном изготовлении шариков большие из них тормозят, а меньшие ускоряют сепаратор. Между сепаратором и шариками могут возникать значительные давления и силы трения. С этим связаны износ шариков и сепараторов, увеличение потерь в подшипнике и случаи поломки сепараторов. Динамика подшипника. Вредное влияние динамических факторов больше всего проявляется в упорных подшипниках. Поэтому допускаемые частоты вращения для упорных подшипников значительно ниже, чем для радиально и радиально-упорных. Смазка подшипников. Она уменьшает трение, снижает контактные напряжения, защищает от коррозии, способствует охлаждению подшипника. Излишнее количество масла ухудшает работу подшипника.
Можно отметить следующие основные причины потери работоспособности подшипников качения. Усталостное выкрашивание наблюдается у подшипников после длительного времени их работы в нормальных условиях. Износ наблюдается при недостаточной защите от абразивных частиц. Износ является основным видом разрушения подшипников автомобильных, тракторных, горных, строительных и подобных машин. Разрушение сепараторов дает значительный процент выхода из строя подшипников качения, особенно быстроходных. Раскалывание колец и тел качения связано с ударными и вибрационными перегрузками, неправильным монтажом, вызывающим перекосы колец, заклинивание и т.п. Остаточные деформации на беговых дорожках в виде лунок и вмятин наблюдаются у тяжелонагруженных тихоходных подшипников.
Современный расчет подшипников качения базируют только на двух критериях: расчет на статическую грузоподъемность по остаточным деформациям; расчет на ресурс (долговечность) по усталостному выкрашиванию.
Выбор подшипников по динамической грузоподъемности С. Условие подбора:
С (потребная) ≤ С (паспортная)
При этом под С понимают радиальную силу для радиальных и радиально-упорных подшипников, осевую силу для упорных и упорно-радиальных. Динамическая грузоподъемность и ресурс связаны эмпирической зависимостью:
L = a1a2 (C/P) p
L - ресурс, а1 - коэффициент надежности, а2 - обобщенный коэффициент совместного влияния качества металла и условий эксплуатации, р=3 - для шариковых и р=3,33 - для роликовых подшипников.
Если частота вращения постоянна, ресурс удобнее считать в часах: Lh = L106/ (60n).
Эквивалентная динамическая нагрузка Р для радиальных и радиально-упорных подшипников есть такая условная постоянная радиальная сила Рr, которая при приложении ее к подшипнику с вращающимся внутренним кольцом обеспечивает такую же долговечность, какую подшипник имеет при действительных условиях нагружения.
Рr = (XVFr + YFa) KбKT; Рa = (XFr + YFa) KбKT
По статической грузоподъемности: Р0 ≤ С0; Р0 - эквивалентная статическая нагрузка. С0 - статическая грузоподъемность (из справочника).
Лично наблюдал износ подшипников автомобиля, из-за попадание пыли и грязи.